Gravitationsgesetz

Universelle Kraft

Im Jahr 1687 veröffentlichte der englische Physiker und Mathematiker Isaac Newton (1642 – 1726) die “Philosophiae Naturalis Principia Mathematica” und sein absolut revolutionäres Konzept einer universellen Gravitationskraft.

Erstmals wurde die Anziehungskraft der Erde, wie sie auf einen Apfel wirkt, mit dem gleichen universellen Gesetz beschrieben, wie für die Anziehungskraft der Erde auf den Mond.

Die Gravitationskraft gilt generell zwischen zwei Massen jeglicher Grösse. Sie gilt zwischen der Erde und einem Apfel, wie auch zwischen der Erde und dem Mond.

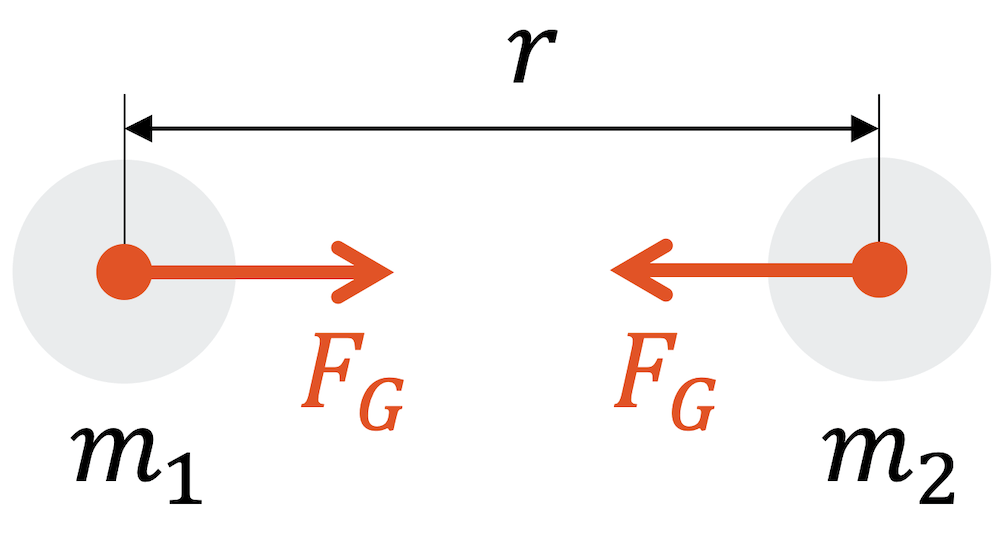
Die beiden (unterschiedlichen) Massen ziehen sich mit der gleichen Gravitationskraft \(F_G\) gegenseitig an. Der Betrag der Kraft ist proportional zu den beiden Massen \(m_1\) und \(m_2\) und umgekehrt proportional zum Quadrat des Abstands \(r\):

\[ F_G = G \cdot \frac{m_1 \cdot m_2}{r^2} \quad \quad \text{mit} \quad \quad G=6.674 \cdot 10^{-11} \; \frac{\text{m}^3}{\text{kg}\;\text{s}^2} \]

Wenn wir eine der beiden Massen verdoppeln, verdoppelt sich auch die Gravitationskraft, denn die Kraft eines Kilogramms und die Kraft eines weiteren Kilogramms addieren sich und wir kriegen die doppelte Kraft.

Mit dem Abstand ist es so, dass die Kraft mit grösser werdendem Abstand sehr schnell schwächer wird. Verdoppeln wir den Abstand, so ist die Kraft nicht nur halb so gross. Sie wird sogar mit dem Faktor \(\frac{1}{2^2} = \frac{1}{4}\), also vier Mal kleiner! Anders herum, nimmt die Kraft bei kleinerem Abstand quadratisch zu.

\(G\) steht für die universell geltende Gravitationskonstante. Es ist eine konstante Zahl mit Einheiten, die im ganzen Universum gleichermassen gilt.

Unterschied zur Gewichtskraft

Wir kennen ja die Gewichtskraft \(F_g\), die mit der Masse \(m\) und der Erdbeschleunigung \(g\) berechnet wird:

\[ F_g = m \cdot g \]

Das ist die gleiche Kraft! Die Gewichtskraft kommt aufgrund der Anziehung der Erde zustande. Sie ist die Gravitationskraft! Was ist jetzt der Unterschied oder warum haben wir zwei Formeln für die gleiche Kraft?

Die Gewichtskraft berechnet sich mit der Erdbeschleunigung \(g = 9.81\,\frac{\text{m}}{\text{s}^2}\). Diese entsteht wegen der Gravitationskraft, d.h. der Anziehung der beiden Massen, dem Objekt und der Erde.

In der Nähe der Erdoberfläche lässt sich diese Kraft mit \(g\) sehr einfach berechnen. Solange wir auf der Erde bleiben, behalten wir mehr oder weniger den gleichen Abstand zum Schwerpunkt der Erde. Die Erdbeschleunigung bleibt deshalb ziemlich konstant.

Sobald wir die Erde verlassen, fällt der zunehmende Abstand immer mehr ins Gewicht und die Kraft nimmt ab. Wir müssten in diesem Fall die Erdbeschleunigung kleiner machen, als \(9.81\,\frac{\text{m}}{\text{s}^2}\). Das wäre wiederum sehr unpraktisch.

Wären wir sehr weit von der Erde entfernt oder wären wir in der Nähe eines grösseren Himmelskörpers (z.B. Jupiter oder gar die Sonne), dann müssten wir \(g\) wieder grösser machen. Von der “Erdbeschleunigung” zu sprechen würde definitiv keinen Sinn mehr geben.

In all diesen Fällen benutzen wir die Gravitationskraft \(F_G\):

\[ F_G = G \cdot \frac{m_1 \cdot m_2}{r^2} \]

Berechnung der Erdmasse

Auf der Erdoberfläche, fällt ein Gegenstand der Masse \(m\) mit der Gewichtskraft \(F_g=m \cdot g\). Die Erdbeschleunigung \(g\) hat den Wert, den wir in Fallexperimenten messen können:

\[ g=9.81\;\frac{\text{m}}{\text{s}^2} \]

Da die Gewichtskraft nichts anderes als die Gravitationskraft ist, die zwischen der Masse \(m\) und der Erdmasse \(m_E\) wirkt, lautet die Gravitationskraft in diesem Fall:

\[ F_G=G \cdot \frac{m_E m}{r_E^2} \]

Dabei ist \(r_E\) der Radius der Erde und damit auch Abstand der beiden Schwerpunkte.

Wenn beide Kräfte \(F_g\) und \(F_G\) die Gleichen sind, können wir sie auch gleichsetzen (und \(m\) kürzen):

\[ F_G \quad = \quad G \cdot \frac{m_E \cancel{m}}{r_E^2} \quad = \quad \cancel{m} \cdot g \quad = \quad F_g \]

Wir lösen nach der Masse der Erde \(m_E\) auf und setzen die Erdbeschleunigung \(g\), den Erdradius \(r_E\) und die Gravitationskonstante \(G\) ein:

\[ m_E = \frac{g\,r_E^2}{G} = \frac{9.81\,\frac{\text{m}}{\text{s}^2} \;\; \cdot \;\; (6.371\cdot10^6\,\text{m})^2}{6.674\cdot10^{-11}\,\frac{\text{m}^3}{\text{kg}\,\text{s}^2}} \quad = \quad 5.97\cdot10^{24}\,\text{kg} \]

Newtons Gedankenexperiment

Der Legende nach, soll Newton im Obstgarten auf die Idee gekommen sein, dass der Apfel und der Mond dem gleichen Naturgesetz unterworfen sind. Newtons Gravitationstheorie und die damit verbundenen drei Newtonschen Gesetze galten erstmals für irdische und himmlische Körper zugleich, was für die damalige Zeit mehr als bahnbrechend war.

Die grösste Frage, die damals niemand beantworten konnte, war: “Warum fällt der Apfel und der Mond nicht?”

Mit Hilfe seines Gedankenexperiments kam Newton auf die geniale Idee:

In seinem Gedankenexperiment überlegt sich Newton, wie eine Kanone auf einem hohen Berg eine Kugel abschiesst. Die Kanonenkugel würde irgendwo am Fusse des Berges herunterfallen (gleich wie ein Apfel), denn Ihre Flugbahn ist zur Erde hin gekrümmt.

Schiesst die Kanone die Kugel stärker ab, fliegt sie weiter. Je stärker sie schiesst, desto weiter fliegt die Kugel, aber sie fällt immer wieder auf die Erde herunter.

Wenn die Kugel genug schnell abgeschossen wird, kommt die Krümmung der Erde mit ins Spiel. Ist die Erde etwa gleich stark gekrümmt wie die Flugbahn, kann die Kanonenkugel die Erdoberfläche gar nie mehr erreichen. Sie fällt andauernd und kommt nie an. ????

Heute wissen wir natürlich, dass dieses Gedankenexperiment vom Prinzip her funktioniert: Satelliten oder die internationale Raumstation ISS fliegen in dieser Art um die Erde herum. Sie sind in einer Umlaufbahn und ja, sie fallen dauernd, ohne jeweils aufzuschlagen. ????️

Die Erde hat einen natürlichen Satelliten, den Mond. Auch der Mond befindet sich auf einer Umlaufbahn und auch er fällt, ohne auf der Erdoberfläche anzukommen.

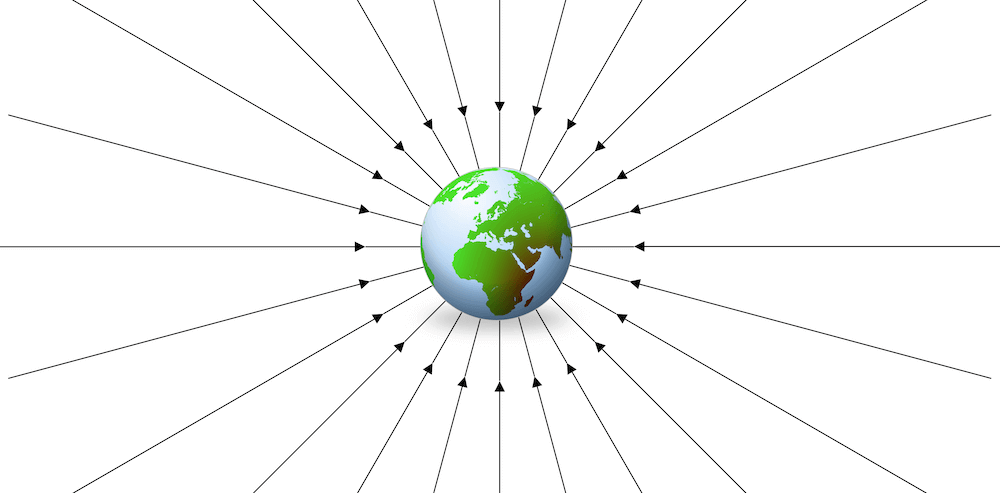
Gravitationsfeld

Das Gravitationsfeld ist die Fernwirkung der Gravitation einer Masse auf ihre Umgebung. Es kann mit Hilfe eines sog. Feldlinien-Diagramms dargestellt werden.

Detailliertere Informationen dazu findest du im Artikel zum Gravitationsfeld.

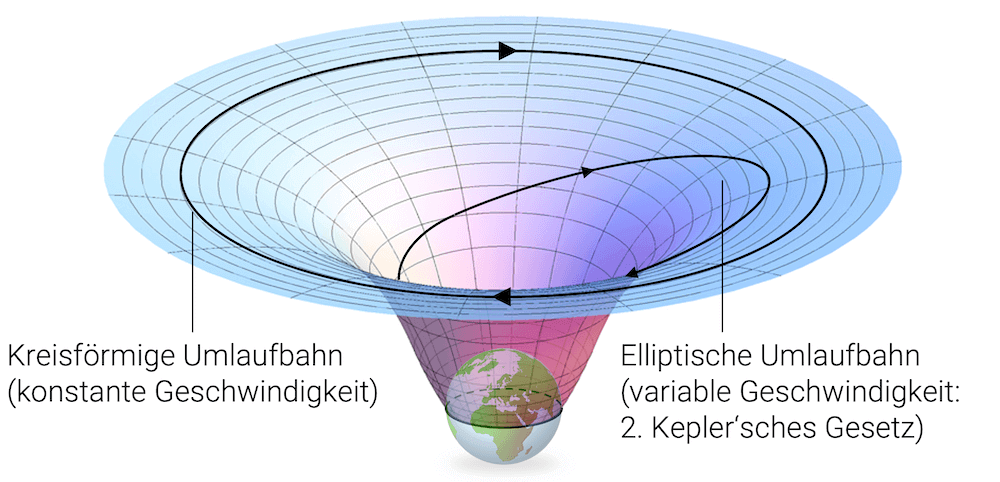
Gravitationspotenzial und Potenzialtopf

Unter dem Potenzialtopf wird die Absenkung der potenziellen Energie in der Nähe der Masse verstanden, die im Potenzialdiagramm wie eine “Vase” oder eben wie ein “Topf” aussieht. Um die Masse und damit den “Topf” verlassen zu können, muss gegen die Gravitationskraft Hubarbeit verrichtet werden. Das Verlassen des Potenzialtopfs braucht deshalb eine gewisse Energie.

Detailliertere Informationen dazu findest du im Artikel zum Gravitationspotenzial.

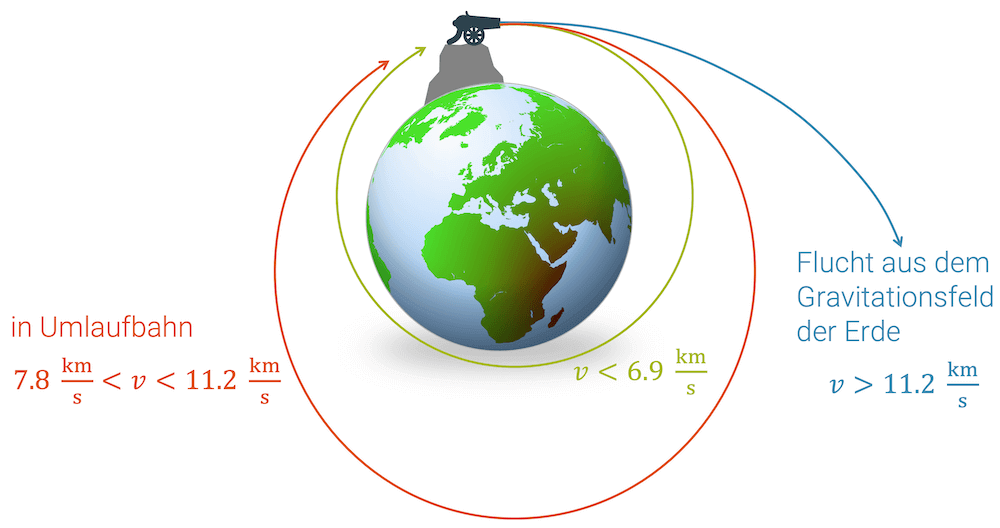
Fluchtgeschwindigkeit

Die Fluchtgeschwindigkeit ist die Geschwindigkeit, die nötig ist, um mit der damit verbundenen kinetischen Energie den Potenzialtopf eines Planeten oder Monds verlassen zu können. Sie ist die minimale Geschwindigkeit, die ein Objekt haben muss, um die Gravitationskraft zu überwinden.

Auf der Erde beträgt diese Geschwindigkeit 11.2 Kilometer pro Sekunde, was umgerechnet über 40’000 km/h ergibt!

Detailliertere Informationen dazu findest du im Artikel zur Fluchtgeschwindigkeit.

Herleitung Gravitationsgesetz

Newton hat für das Aufstellen des Gravitationsgesetzes auf Keplers Drittes Gesetz aufgebaut, welches letztlich nichts anderes ist als die Erhaltung des Drehimpulses.

\[ \Big(\frac{T_1}{T_2}\Big)^2 = \Big(\frac{a_1}{a_2}\Big)^3 \]

Die Breiten der Ellipsenbahnen \(a_1\) und \(a_2\) von zwei Himmelskörpern stehen in einem bestimmten Verhältnis zu den Perioden \(T_1\) und \(T_2\), die diese um den gleichen zentralen Körper haben. Der Himmelskörper auf der grösseren Ellipse hat eine grössere Periode als der innere Himmelskörper.

Nehmen wir die Sonne als zentralen Massepunkt und vergleichen wir die Erde und den Mars. Wir nehmen weiter an, dass sich die Planeten alle in einem Kreis um die Sonne bewegen, so gilt Keplers Gesetz auch für die Abstände \(r\) der Planeten zur Sonne. Statt 1 und 2 setzen wir jetzt die Anfangsbuchstaben von Erde und Mars:

\[ \Big(\frac{T_E}{T_M}\Big)^2 = \Big(\frac{r_E}{r_M}\Big)^3 \]

Wir schreiben die vorige Gleichung etwas um und erzeugen damit Brüche mit den Werten der einzelnen Planeten.

\[ \frac{T_E^2}{r_E^3} = \frac{T_M^2}{r_M^3} = \frac{T_J^2}{r_J^3} = … = C_S \]

Da der Bruch gleich ist, egal um welchen Planeten es sich handelt, können wir ihn für die Erde, für Mars, oder sogar für Jupiter aufstellen etc. Alle Brüche haben den gleichen Wert, den wir jetzt einfach mal \(C_S\) nennen.

Das Gemeinsame, was die Planeten haben, ist die Sonne. Wir haben also eine Konstante, die etwas mit unserer Sonne zu tun hat.

Jetzt schauen wir uns die Kraft an, die auf die Erde wirkt. Da wir eine Kreisbewegung um die Sonne haben, können wir die Zentripetalkraft aufstellen. Sie ist für die Kreisbewegung verantwortlich und sie zeigt zum Zentrum des Kreises.

\[ F_Z = m_E r_E \omega^2 \]

Wir ersetzen die Winkelgeschwindigkeit \(\omega\) mit der Bahngeschwindigkeit \(v\) und benutzen dazu die Beziehung \(v = r_E \omega\).

\[ F_Z = m_E r_E \Big( \frac{v}{r_E} \Big)^2 = v^2 \cdot \frac{m_E}{r_E} \]

Jetzt ersetzen wir die Geschwindigkeit mit einem anderen Ausdruck. Die Bahngeschwindigkeit \(v\) ist ja schliesslich nichts anderes als eine Strecke pro Zeit. Genauer: Sie ist der Umfang des Kreises (mit Radius \(r_E\)) pro Periode \(T_E\) (1 Jahr für einmal um die Sonne herum):

\[ v = \frac{2 \pi r_E}{T_E} \]

Wir ersetzen \(v\) mit dem obigen Ausdruck und erhalten

\[ F_Z = \Big( \frac{2 \pi r_E}{T_E} \Big)^2 \cdot \frac{m_E}{r_E} = \frac{4 \pi^2 r_E^{\cancel{2}}}{T_E^2} \cdot \frac{m_E}{\cancel{r_E}} = \frac{4 \pi^2 m_E r_E}{T_E^2} \]

Jetzt ersetzen wir die quadrierte Periode \(T_E^2\) mit dem Ausdruck \(\frac{T_E^2}{r_E^3} = C_S\) von oben: \(T_E^2 = C_S \cdot r_E^3\). Wir können wieder mit \(r_E\) kürzen:

\[ F_Z = \frac{4 \pi^2 m_E r_E}{C_S r_E^3} = \frac{4 \pi^2 m_E}{C_S r_E^2} \]

Die Funktion der Zentripetalkraft, die wir berechnet haben, wird im Beispiel “Erde um Sonne” von der Gravitationskraft übernommen. Wir schreiben deshalb \(F_G = F_Z\).

Newton hat zusätzlich noch die Masse der Sonne \(m_S\) sowohl im Zähler, wie im Nenner eingeführt. Der Ausdruck in der Klammer ist konstant und damit eine universelle Grösse – das beweisen wir an dieser Stelle nicht – sie wird deshalb einfach mit \(G\) abgekürzt, was uns die Gravitationskonstante gibt.

\[ F_G = F_Z = \Big( \frac{4 \pi^2}{C_S m_S} \Big) \cdot \frac{m_S m_E}{r_E^2} = G \cdot \frac{m_S m_E}{r_E^2} \]

Jetzt haben wir Newtons Gravitationsgesetz gefunden:

\[ F_G = G \cdot \frac{m_1 m_2}{r^2} \]

Beachte, dass dieses Gesetz nicht nur für die Sonne und ihre Planeten gilt, sondern auch für das schwarze Loch im Zentrum unserer Galaxie, um welches die Sterne und ihre Planeten kreisen, oder für die Erde als Zentrum, um welches der Mond und die vielen Satelliten kreisen. Es ist ein universelles Gesetz. ????

Die Gravitationskraft ist die Schwächste aller Kräfte

An der Gravitationskonstante \(G\) erkennen wir auch, dass die Gravitationskraft sehr klein ist.

\[ G=6.674 \cdot 10^{-11} \; \frac{\text{m}^3}{\text{kg}\;\text{s}^2} \]

Sie hat den Exponenten \(10^{-11}\): Das sind Hunderstel von einem Nano!

\[ 10^{-11} = 0.000’000’000’01 \]

Tatsächlich ist die Gravitationskraft bei weitem die Schwächste der vier Grundkräfte der Physik. Selbst die schwache Kraft, die wirklich sehr schwach ist, ist immer noch um Grössenordnungen stärker.

In der Teilchenphysik wird die Gravitationskraft meistens weggelassen, weil sie im Vergleich zu den anderen Grundkräften der Physik vernachlässigbar klein ist: Ein freies Proton spürt viele andere Kräfte, bevor es aufgrund seiner Gewichtskraft “auf den Boden fällt”.

Simulation

• Simulation zu Newtons Gedankenexperiment