Gewichtskraft

Masse vs. Gewichtskraft

Die Gewichtskraft ist die Kraft, mit welcher die Erde aufgrund der Gravitation eine Masse anzieht. Diese Anziehungskraft führt auch dazu, dass eine Masse immer im freien Fall zu Boden fallen wird. Wir wissen vom freien Fall, dass Gegenstände, unabhängig von ihrer Masse, alle mit der Erdbeschleunigung \(g\) fallen. Mit Newton 2 (\(F = m \cdot a\)) wissen wir, dass die Masse \(m\) mal die Beschleunigung \(a\) die Kraft \(F\) ergibt, die es braucht, um die Masse so zu beschleunigen. Wir setzen deshalb für die Beschleunigung \(a\) die Erdbeschleunigung \(g\) ein und erhalten für die Gewichtskraft \(F_g\):

\[ F_g = m \cdot g \]

Der Betrag der Gewichtskraft \(F_g\) wird aus dem Produkt von Masse \(m\) und Erdbeschleunigung \(g=9.81\,\frac{\text{m}}{\text{s}^2}\) berechnet. Die Richtung der Gewichtskraft ist immer zum Zentrum der Erde gerichtet. Das Zentrum der Erde ist ihr Schwerpunkt, der stellvertretend für die ganze Masse der Erde steht. Die Gewichtskraft greift deshalb auch am Schwerpunkt der Masse. In der nachfolgenden Abbildung ist das ein Punkt etwa in der Mitte des Männchens.

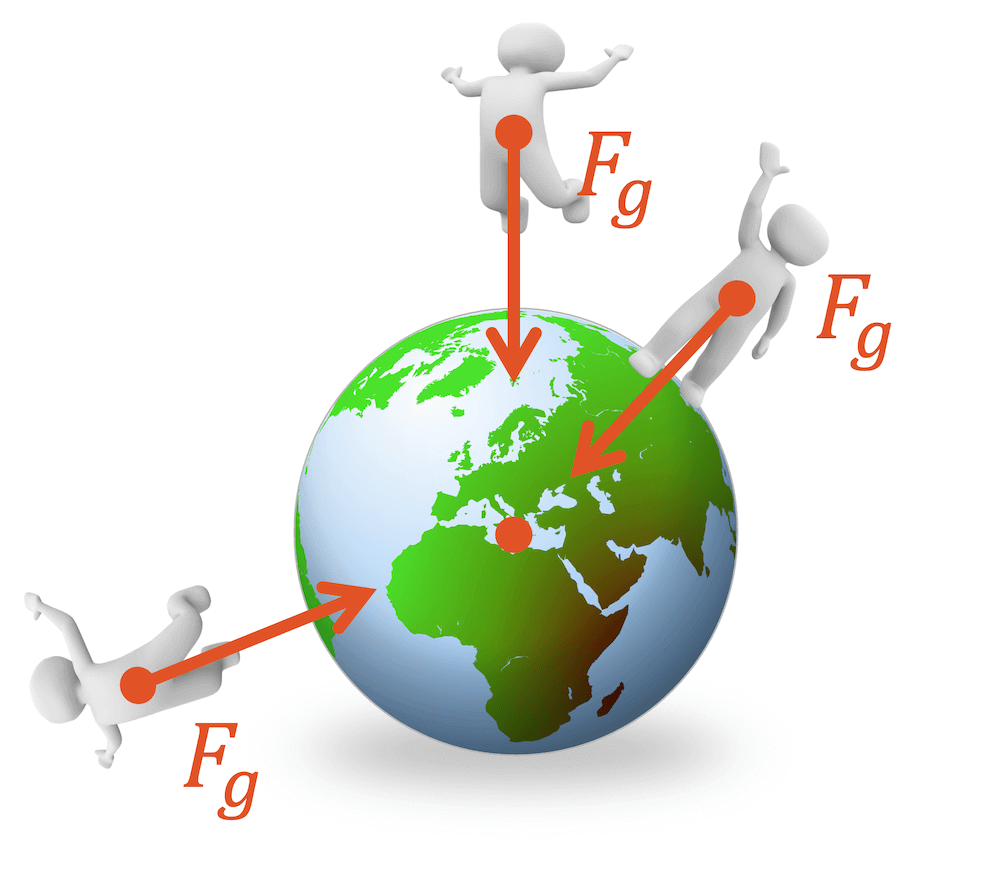
Wenn wir in der Küche unsere Zutaten mit der Küchenwaage wägen, misst die Waage eigentlich die Gewichtskraft. Die Waage misst nämlich die Kraft mit welcher die Zutaten auf ihren Sensor drücken. Wir können dies ja schnell sehen, wenn wir beispielsweise die Zutaten wegnehmen und einfach nur mit den Fingern drücken – schon misst sie etwas, nämlich die Normalkraft, mit welcher wir drücken.

Die Waage zeigt jetzt aber eine Masse in Gramm an. Misst sie jetzt die Gewichtskraft oder die Masse?

Sie misst eine Kraft und rechnet sie bereits schon mit der Erdbeschleunigung um, denn die Einheit Newton hat sich im Alltag nie durchgesetzt. Die Anzeige sagt uns, welche Masse wir haben müssten, aufgrund der vom Sensor gemessenen Kraft.

Wenn wir von Gewicht reden, meinen wir eigentlich die Gewichtskraft. Auf der Erdoberfläche gilt die Erdbeschleunigung \(g\) und somit funktioniert auch die Waage. Wenn wir aber die Stoffmenge meinen, sollten wir von Masse reden. Im Weltall wäre ein Kilogramm Mehl immer noch ein Kilogramm Mehl, jedoch hätte es keine Gewichtskraft mehr, da dort \(g=0\) herrscht. Die Waage würde auch 0 g anzeigen.

Da die Physik eine universell gültige Wissenschaft ist und nicht nur auf der Erde gültig sein kann, müssen wir von jetzt an zwischen Gewichtskraft und Masse unterscheiden.

Gewichtskraft ausserirdisch

Wie ist die Gewichtskraft, wenn wir mal nicht auf der Erde sind? Die Erdbeschleunigung gilt ja nur in einem relativ schmalen Bereich um die Erdoberfläche herum. Würden wir ein sehr tiefes Loch graben, würde sie wieder abnehmen. Im Zentrum der Erde wäre sie sogar null. In grosser Höhe nimmt die Erdbeschleunigung und damit die Gewichtskraft ebenfalls ab. Im Weltall, weit weg von der Erde, wären wir schwerelos. Wir hätten immer noch unsere Masse, aber es liesse sich keine Gewichtskraft mehr feststellen.

Da der Mond eine viel kleinere Masse als die Erde hat, ist die Fallbeschleunigung auf dem Mond auch kleiner und zwar rund 6-mal kleiner. Die gleiche Masse \(m\) wird auf dem Mond mit der Fallbeschleunigung für die Mondoberfläche \(g_M\) berechnet, die rund 6-mal kleiner ist als \(g\):

\[ g_M \approx \frac{g}{6} \approx 1.6\,\frac{\text{m}}{\text{s}^2} \]

Für die Gewichtskraft auf dem Mond \(F_{gM}\) erhalten wir deshalb auch die rund 6-mal kleinere Gewichtskraft:

\[ F_{gM} = m \cdot g_M \quad \approx \quad \frac{F_g}{6} \]

Auf einem grossen Planeten oder auf der Sonnenoberfläche wäre die Gravitationskraft um Faktoren grösser als auf der Erde. Auf der Sonnenoberfläche beträgt die Fallbeschleunigung \(g_S \approx 274\,\frac{\text{m}}{\text{s}^2}\). Unsere Waage mit unserem Kilogramm Mehl würde (mal von der hohen Temperatur abgesehen) eine 28-fache Gewichtskraft messen und somit “28 kg” anzeigen. Das ist natürlich Quatsch! Es sind immer noch 1 kg, aber die Gewichtskraft ist jetzt \(F_{gS}=274\,\text{N}\) statt \(F_g = 9.81\,\text{N}\).Video