Das Innen und das Aussen ist durch die Systemgrenze definiert. Wir meinen damit aber nicht unbedingt das rein Lokale, sondern was von aussen kommt (was nicht zum System gehört) und was rein intern ist. Auf die Kräfte bezogen heisst das:
- Äussere Kräfte sind solche, die von aussen auf unser System wirken. Meistens greifen sie an den Systemgrenzen an, z.B. durch Druck oder Zug, aber sie können auch auf den Schwerpunkt wirken, wie z.B. die Gravitationskraft.
- Innere Kräfte wirken von einer anderen Stelle im System. Sie sind so gesehen, eine rein interne Angelegenheit. Sie treten immer als Kräftepaar auf, d.h. sie heben sich in Summe alle auf.
Wenn wir bei der Diskussion von Newtons Erstem Gesetz von der resultierenden Kraft gesprochen haben, haben wir immer nur die äusseren Kräfte berücksichtigt. Das heisst aber nicht, dass es keine innere Kräfte gibt. Die gibt es sehr wohl, jedoch heben sie sich alle auf. Wir können sie deshalb getrost auslassen.
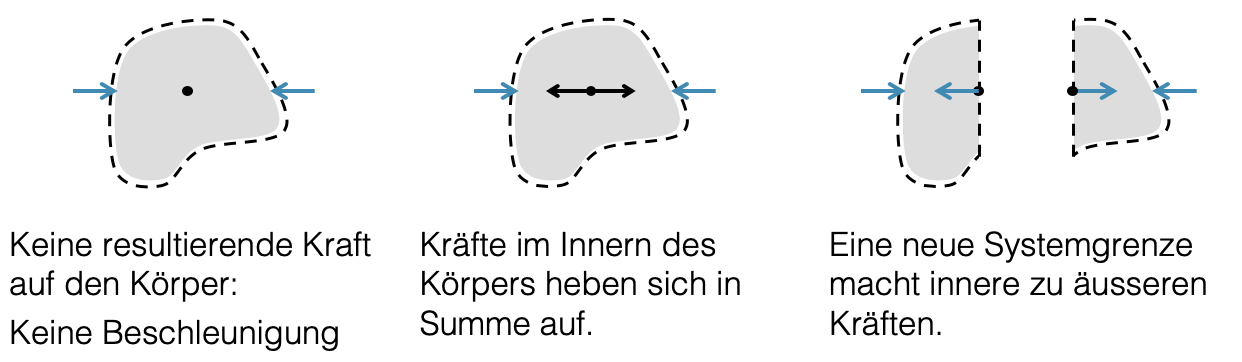
In gewissen Fällen interessiert es uns aber, wie gross die inneren Kräfte sind, z.B. wenn wir herausfinden wollen, ob ein Material die Kraft aushalten oder ob es brechen wird. Da wir nur mit Hilfe der Newtonschen Gesetze zu Gleichungen und damit zu Aussagen kommen, diese aber nicht auf die inneren Kräfte angewendet werden können, weil sie in Summe null sind, gibt es einen anderen Trick: Wir wählen die Systemgrenze so, dass sie genau durch die zu untersuchende Stelle führt. Dadurch werden die inneren Kräfte zu zwei äusseren Kräften.
Wie wissen wir, welche innere Kraft zu welchem Teilsystem zugeordnet werden soll? Überlege ob die Stelle, an welcher die neue äussere Kraft wirken soll, eher einen Druck oder einen Zug verspürt. In unserem Beispiel wird der ganze Körper zusammengedrückt. Es ist deshalb zu erwarten, dass an der Stelle, wo wir die neue Grenze gezogen haben, eher ein Druck verspürt wird. Somit muss die neue äussere Kraft für das linke Teilsystem nach links zeigen. Für das rechte Teilsystem nehmen wir die andere Kraft nach rechts.
Schliesslich muss die neue äussere Kraft, zusammen mit der ursprünglichen äusseren Kraft, das Kräftegleichgewicht bewahren. Die beiden müssen entgegengesetzt sein, damit \(F_{res}=0\), was die Richtung eindeutig festlegt.
Beispiel
Das Mädchen auf dem Fahrrad steht in Ruhe. Die resultierende Kraft verschwindet, denn die Gewichtskraft wird durch zwei Normalkräfte und zwei Reibungskräfte aufgehoben.
Wie können Sei eine Aussage über die Kraft machen, die in der vorderen Gabel herrscht?
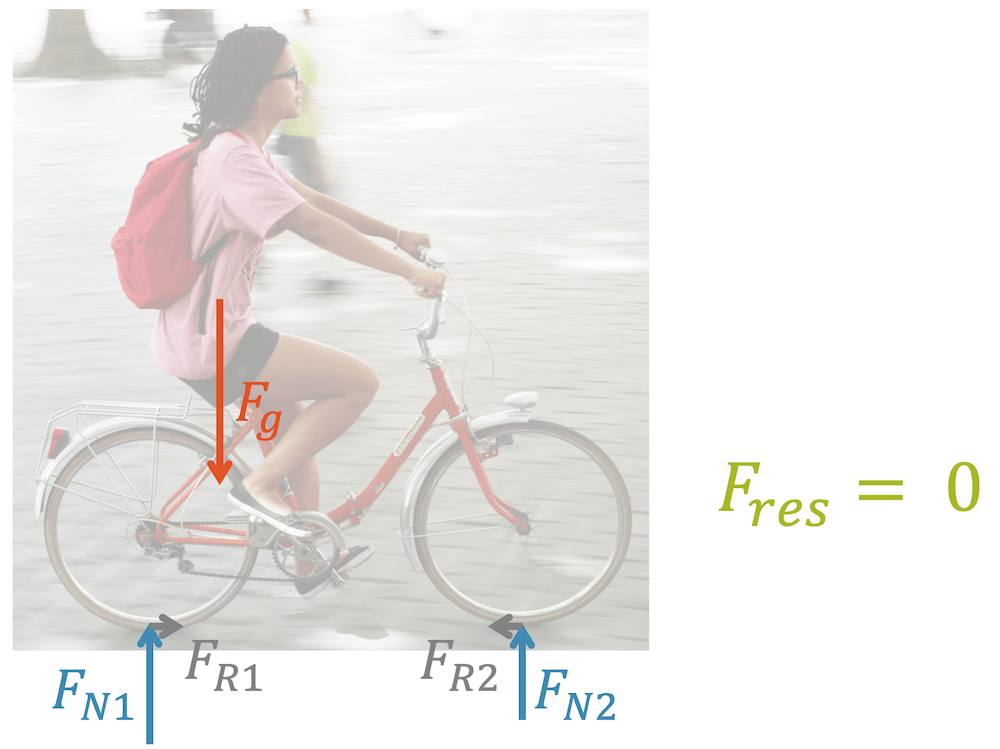
Image by Carlos ZGZ, licensed under CC BY-SA 2.0
Wir “schneiden” die vordere Gabel durch und ziehen die Systemgrenze durch den zu betrachtenden Punkt A. Die innere Kraft war Teil eine Kräftepaars. Jetzt wird eine Kraft auf das System “Mädchen + Velo” und die andere Kraft auf das System “Gabel + Vorderrad”. Beide Teilsysteme sind weiterhin im Kräftegleichgewicht, d.h. für beide Systeme gilt \(F_{res}=0\). Denn unser “Schnitt” war rein theoretisch. Hätten wir tatsächlich mit der Säge an der Gabel geschnitten, so hätten wir die Gabel in ihrer Struktur geschwächt. Sie könnte die innere Kraft nicht mehr aufrecht erhalten und das Velo würde auseinanderbrechen.
Durch die Trennung der beiden Teilsysteme ist für das Teilsystem “Mädchen + Velo” ein Teil der Gewichtskraft, die vordere Normalkraft, sowie die kleine Reibungskraft am Vorderrad weggefallen. Dieser Wegfall muss durch die Kraft im Punkt A kompensiert werden, damit weiterhin \(F_{res}=0\) gilt.
Für das andere Teilsystem sind nur die Kräfte am Vorderrad geblieben und die anderen sind weggefallen. Damit wir aber auch hier \(F_{res}=0\) erhalten, brauchen wir eine Kraft, die in Summe gleich gross ist, aber entgegengesetzt in der Richtung bzw. in ihrem Vorzeichen.
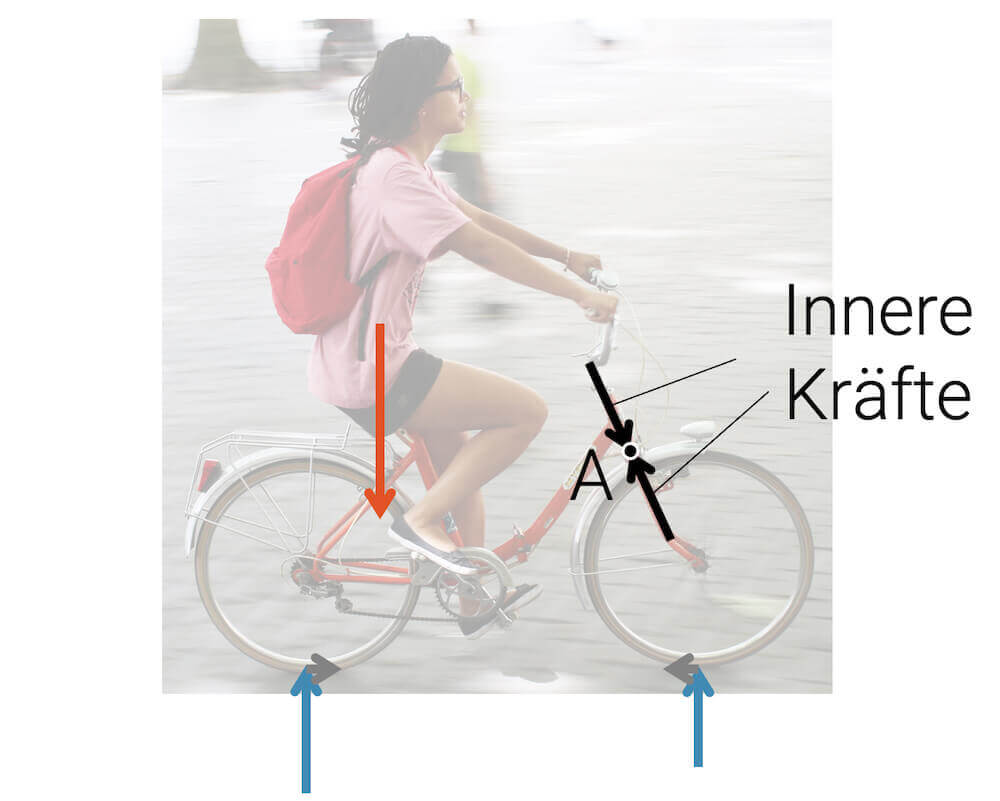
Image by Carlos ZGZ, licensed under CC BY-SA 2.0
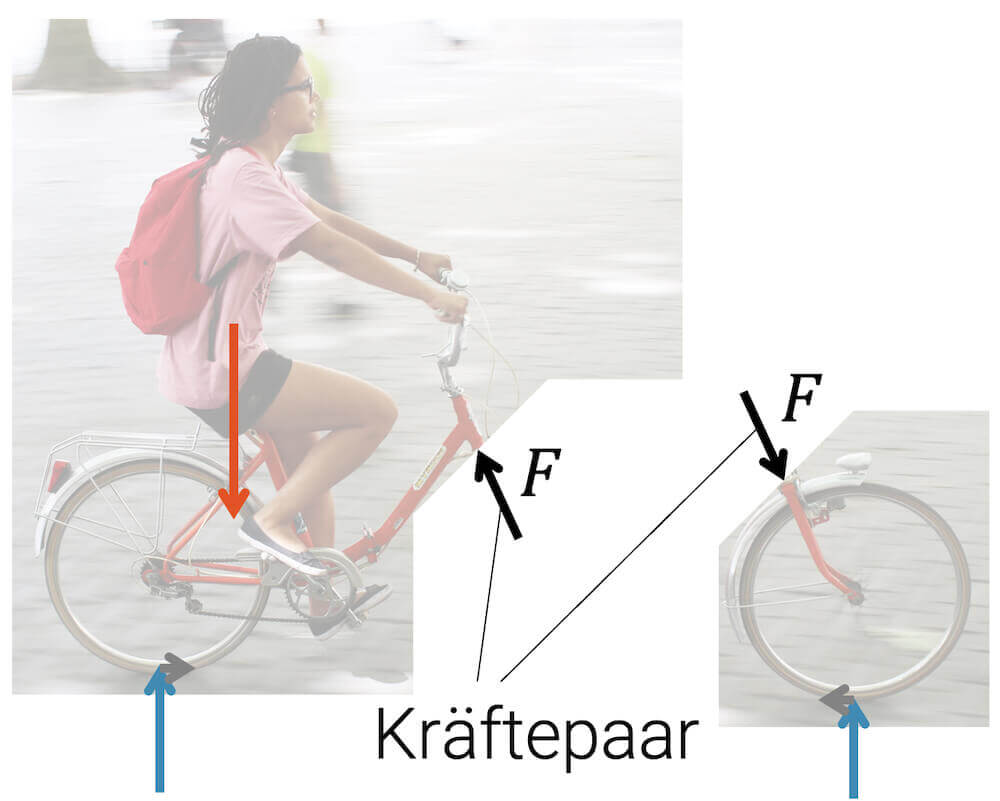
Image by Carlos ZGZ, licensed under CC BY-SA 2.0
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.