Senkrechter Wurf

Wir können uns den senkrechten Wurf am Beispiel des Genfer “jet d’eau” erklären, einem 140-Meter-Springbrunnen. Das Wasser verlässt die Düse mit hoher Geschwindigkeit. Wir betrachten einen Wassertropfen. Gleich von Anfang nimmt die Geschwindigkeit aber schnell ab und der Körper erreicht irgendwann die maximale Höhe von 140 Metern. Der Wassertropfen ist komplett abgebremst und schwebt einen kurzen Moment still. Ab jetzt kommt der freie Fall nach unten. Die Geschwindigkeit nach unten nimmt jetzt immer mehr zu.

Dieser scheinbar komplexe Bewegungsablauf ist die direkte Folge einer konstanten, nach unten gerichteten Beschleunigung, der Erdbeschleunigung. Sie ist verantwortlich für das Zunehmen der Geschwindigkeit nach unten. Da die Erdbeschleunigung nach unten gerichtet ist, baut sie Geschwindigkeiten nach unten auf. Am Anfang ist die Geschwindigkeit jedoch nach oben gerichtet. Die nach unten gerichtete Beschleunigung ist der Geschwindigkeit entgegen gesetzt und baut sie deshalb ab. Der Wassertropfen wird auf dem Weg nach oben abgebremst, bis er kurz still steht.

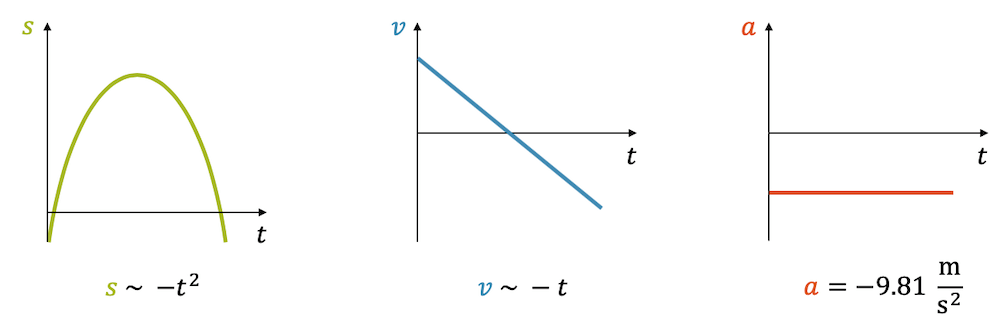
In den Bewegungsdiagrammen sehen wir den Zusammenhang der Bewegung mit der Erdbeschleunigung sehr schön. Im s,t-Diagramm sehen wir, wie der Wassertropfen nach oben geht (zunehmende Position \(s\)) und das bis zu einer maximalen Höhe. Die Geschwindigkeit, die im s,t-Diagramm als Steigung abgelesen wird, nimmt bis zur maximalen Höhe stetig ab. In der maximalen Höhe ist die Geschwindigkeit null, da der Verlauf im maximalen Punkt eine horizontale Tangente hat, d.h. die Steigung ist null.

Im zweiten Teil der Bewegung ist die Steigung negativ. Sie nimmt im Betrag immer mehr zu, d.h. sie wird immer stärker negativ.

Im v,t-Diagramm sehen wir, wie eine anfänglich grösste Geschwindigkeit immer mehr abnimmt, dann kurzzeitig null ist und dann negativ wird, was eine Rückkehr bedeutet. Da \(s\) in der Richtung nach oben definiert worden ist, bedeutet eine positive Geschwindigkeit eine Bewegung nach oben und eine negative Geschwindigkeit eine Bewegung nach unten. Auffallend ist auch, dass die Geschwindigkeit einen linearen Verlauf hat mit konstanter, negativer Steigung.

Die Steigung im v,t-Diagramm entspricht der Beschleunigung. Da diese konstant negativ ist, zeigt das a,t-Diagramm einen konstant, negativen Wert für \(a\) für die ganze Zeit des Wurfs, egal ob nach oben steigend oder nach unten fallend. Der Wert dieser Beschleunigung beträgt, abgesehen von sehr kleinen Abweichungen, überall auf der Erde 9.81\)\frac{\text{m}}{\text{s}^2}\) und wird Erdbeschleunigung genannt.