Schräger Wurf

Schräger Wurf als zusammengesetzte Bewegung 

Der schräge Wurf hat seinen Namen von der Tatsache, dass ein Körper mit einer beliebig gerichteten, zur Horizontalen schräg gerichteten Anfangsgeschwindigkeit abgeschossen werden kann und von da an eine bestimmte Bewegung beschreibt. Um den schrägen Wurf zu verstehen, schauen wir uns wieder die Überlagerung von zwei zusammengesetzten Bewegungen an.

Grundsätzlich kann der schräge Wurf als Zusammensetzung von zwei waagrechten Würfen betrachtet werden. Einfacher ist jedoch die Überlagerung von einer gleichförmigen horizontalen Bewegung mit konstanter Geschwindigkeit (blaue Geschwindigkeitsvektoren) und der Bewegung eines senkrechten Wurfs (rote Geschwindigkeitsvektoren).

Überlagert man die beiden Bewegungen, so müssen die Geschwindigkeitsvektoren addiert werden. Als Resultat erhalten wir die grünen Geschwindigkeitsvektoren, wie in der obigen Grafik gezeigt. Die grünen Geschwindigkeitsvektoren beschreiben die Wurfparabel, wie wir sie aus Erfahrung kennen.

Berechnung der Bewegung in zwei Dimensionen 

Um die Bewegung analysieren zu können, müssen wir bei einer gegebenen “schrägen” Anfangsgeschwindigkeit \(\vec{v_0}\), erst der horizontale (blaue) Anteil \(v_{x0}\) und der vertikale (rote) Anteil \(v_{y0}\) der Geschwindigkeit ermittelt werden. Beachte dabei, dass die \(y\)-Richtung, der Einfachheit halber, nach unten gerichtet ist.

Für die Bestimmung der \(x\)- und der \(y\)-Komponenten, nehmen wir die trigonometrischen Funkionen und den Steigungswinkel \(\alpha\) zur Hand.

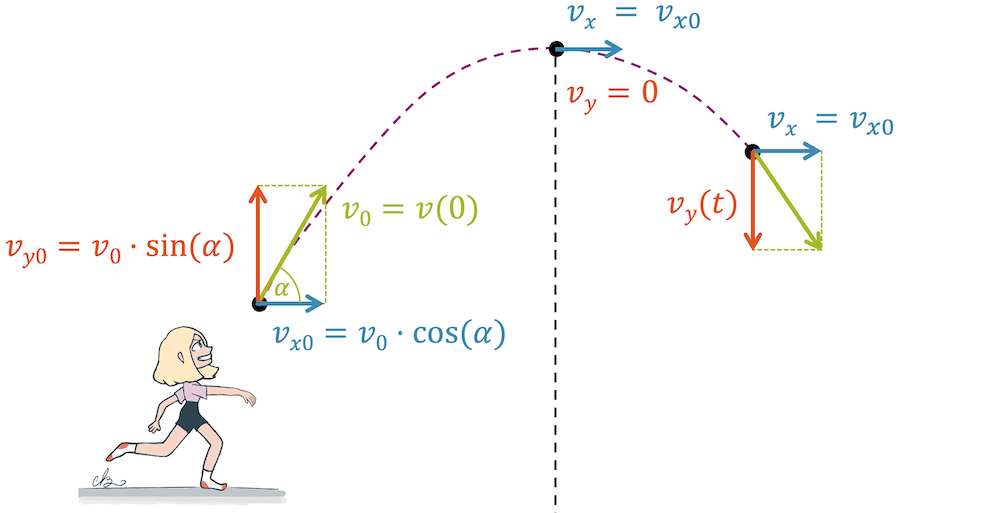
Für die horizontale Komponente \(x(t)\) betrachten wir das rechtwinklige Dreieck mit der Anfangsgeschwindigkeit \(v_0\) (grün) als Hypotenuse und der horizontalen Komponente \(v_{x0}\) (blau) als Ankathete:

\[ \frac{v_{x0}}{v_0}=\cos{\alpha} \]

Wir können so nach \(v_{x0}\) auflösen und damit die horizontale Geschwindigkeitskomponente der Bewegung bestimmen:

\[ v_{x0} = v_0 \cdot \cos{\alpha} \]

Für eine ganz allgemeine horizontale Bewegung, nehmen wir die Bewegungsgleichung (1) für die \(x\)-Position als Funktion der Zeit \(t\):

\[ x(t) = x_0 + v_{x0}t + \frac{1}{2}a_xt^2 \]

Die Startposition können wir in den meisten Fällen auf null setzen, d.h. \(x_0=0\). Die horizontale Geschwindigkeit ist konstant, d.h. wir haben keine Beschleunigung, also \(a_x=0\). Somit vereinfacht sich die Bewegungsgleichung zu:

\[ x(t) = v_{x0} \cdot t \]

Für \(v_{x0}\) können wir die obige Berechnung einsetzen. Wir haben demnach alles was wir brauchen, um die \(x\)-Koordinate der Bewegung als Funktion der Zeit zu berechnen.

Für die vertikale Komponente \(y(t)\) nehmen wir ebenfalls die allgemeine Bewegungsgleichung:

\[ y(t) = y_0 + v_{y0}t + \frac{1}{2}a_yt^2 \]

Auch hier können wir die Anfangsposition \(y_0\) auf null setzen, d.h. \(y_0=0\). Die Anfangsgeschwindigkeit in \(y\)-Richtung erhalten wir wieder mit Hilfe der trigonometrischen Funktionen:

\[ v_{y0} = v_0 \cdot \sin{\alpha} \]

Die Beschleunigung in vertikaler Richtung ist, wie für alle Bewegungen im freien Fall, die Erdbeschleunigung. Beachte, dass die \(y\)-Achse für uns nach oben gerichtet ist. Die Erdbeschleunigung ist aber nach unten gerichtet. Wir müssen deshalb für sie ein negatives Vorzeichen setzen:

\[ a_{y} = -g = -9.81\;\frac{\text{m}}{\text{s}^2} \]

Mit \(y_0\), \(v_{y0}\) und \(a_y\) haben wir ebenfalls alles, was wir brauchen, um die \(y\)-Position als Funktion der Zeit zu berechnen.

Zusammensetzung von zwei waagrechten Würfen 

Der schräge Wurf kann als Kombination von zwei waagrechten Würfen betrachtet werden. Betrachten wir die Bewegung vom höchten Punkt aus, so hat der Gegenstand in diesem Punkt einen kurzen Moment keine vertikale Geschwindigkeit, aber eine konstante horizontale Geschwindigkeit. Es handelt sich deshalb um einen waagrechten Wurf.

Die Bewegung bis zum höchsten Punkt ist auch ein horizontaler Wurf. Benutzen wir die in der Physik sehr übliche Zeitumkehr, d.h. lassen wir einfach den Film rückwärts laufen, so haben wir die gleiche, aber spiegelsymmetrische Bewegung. Sie verläuft vom höchsten Punkt zum Punkt des Abschusses und dort trifft sie in einem bestimmten Winkel zur Horizontalen, auf.