Isothermische Zustandsänderung

Isothermen im p,V-Diagramm

Wenn wir eine Zustandsänderung eines Fluids bei konstanter Temperatur haben, dann bewegt sich der Punkt, der den Zustand im p,V-Diagramm beschreibt, auf einer Isothermen. Die Isothermen sind Linien im p,V-Diagramm, die sämtliche Punkte verbindet, die dem gleichen Temperaturwert entsprechen. Eine Isotherme ist gewissermassen eine Höhenlinie der dreidimensionalen Fläche, die die Zustände \((p,V,T)\) beschreibt. Im p,V-Diagramm schauen wir von “oben” auf diese “Landschaft”. Bewegt sich der Punkt auf einer Isothermen, so verändern sich die “Koordinaten” \((p,V)\), ohne dass sich die dritte “Koordinate” \(T\) ändert.

Für ideale Gase ist der Zusammenhang zwischen den Zustandsgrössen \(p\), \(V\) und \(T\) durch die ideale Gasgleichung gegeben.

\[ pV = nRT \quad \rightarrow \quad p(V)=(nRT) \cdot \frac{1}{V} \]

Isothermen im p-V-Diagramm

Aus der idealen Gasgleichung folgt, dass die Isothermen im p-V-Diagramm Hyperbeln bilden. Für jeden Temperaturwert eine Hyperbel. Je höher die Temperatur, desto weiter oben liegt die Hyperbel.

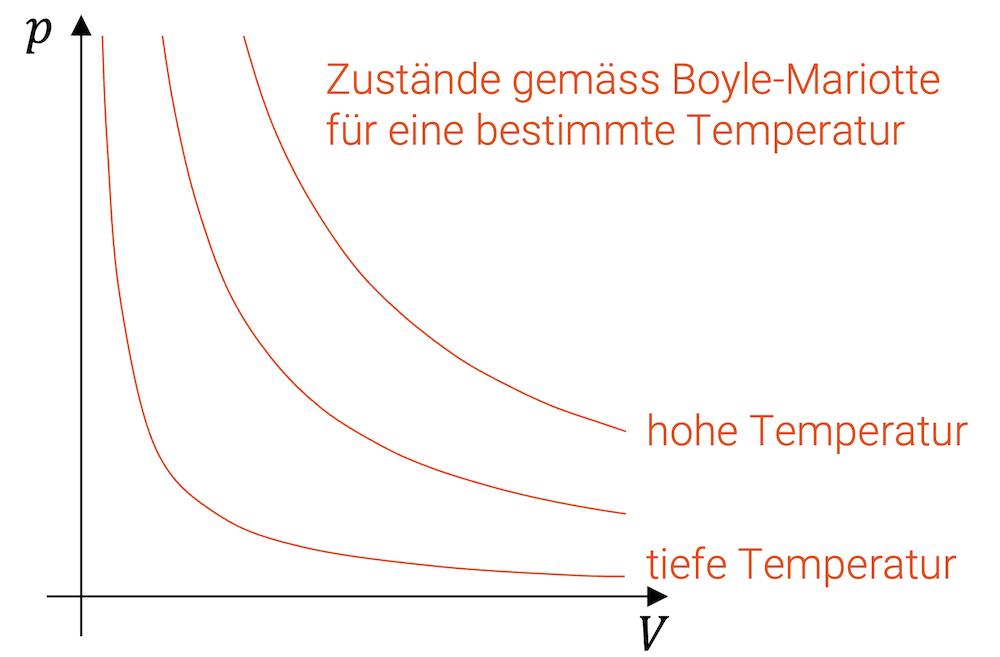
Eine isothermische Zustandsänderung bewegt sich auf der Isothermen der entsprechenden Temperatur. Für ideale Gase entsprechen die Koordinaten \((p,V)\) den Werten gemäss dem Gesetz von Boyle-Mariotte, das eine konstante Temperatur voraussetzt.

Arbeit und Wärme bei isothermischen Zustandsänderungen

Bei einer isothermischen Zustandsänderung ändern Druck und Volumen des Fluids. Die Temperatur bleibt aber konstant.

Die Temperatur ist ein Mass für die innere Energie \(U\). Wenn sie konstant bleibt, bleibt auch die innere Energie konstant:

\[ \Delta U = 0 \]

Bleibt die innere Energie konstant, folgt daraus mit dem Ersten Hauptsatz der Thermodynamik (Energieerhaltung), dass gleich viel Energie zu- wie abgeführt wird.

Bei einer isothermischen Kompression wird am Fluid Arbeit verrichtet, so dass es komprimiert wird. Diese Energiezufuhr muss aber wieder in gleichem Masse weggeführt werden, da sonst die innere Energie zunehmen würde.

Ein Wegführen in Form von Arbeit macht keinen Sinn, weil sie das Fluid wieder entspannen würde. Es wäre einfach ein Rückgängigmachen der Kompressionsarbeit. Die Energie wird in Form von Wärme abgeführt.

\[ W_{in} = Q_{out} \]

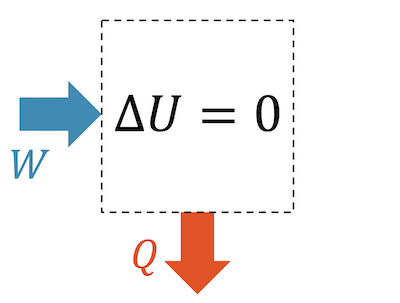
Bei der isothermischen Expansion können wir die gleichen Überlegungen anstellen und daraus schliessen, dass die innere Energie nur konstant bleiben kann (und damit auch die Temperatur), wenn gleich viel Wärme zugeführt wird und in Form von Arbeit abgeführt wird:

\[ Q_{in} = W_{out} \]

Wir können die isothermische Expansion aber auch einfach als die Umkehrung der isothermischen Kompression betrachten.

Diese Zeitumkehrung ist ein beliebtes Werkzeug der Physik und funktioniert auch in diesem speziellen Fall. Allerdings muss beachtet werden, dass viele Zustandsänderungen in der Wärmelehre nicht reversibel sind. Sobald bei der Zustandsänderung Entropie gebildet wird, haben wir einen irreversiblen Prozess, der eine Zeitumkehr nicht mehr zulässt (Zweiter Hauptsatz der Thermodynamik).

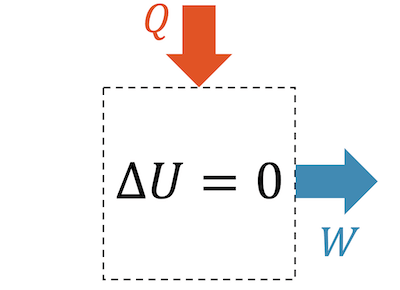
Bei der isothermischen Kompression entspricht die zugeführte Arbeit der abgeführten Wärme:

\[ W_{in} = Q_{out} \]

Bei der isothermischen Expansion gibt das Fluid Arbeit ab, muss aber mit Wärme gespeist werden:

\[ Q_{in} = W_{out} \]

Die zugeführte Arbeit entspricht im p-V-Diagramm der Integrationsfläche unter der Zustandsänderung. Im speziellen Fall der isothermischen Zustandsänderung ist damit automatisch auch die ausgetauschte Wärme mit der Fläche dargestellt, was sonst aber im p-V-Diagramm nicht einfach möglich ist.

\[ W = Q = \int p(V) \; dV \]