Inhalt
Das Wichtigste in Kürze
Die Entropie \(S\) ist eine Zustandsgrösse und ein Mass der Unordnung eines Systems. Je grösser die Unordnung, desto wahrscheinlicher ist der Zustand und desto grösser ist die Entropie.
Die Entropie ist keine Erhaltungsgrösse: Sie kann erzeugt werden.
Zweiter Hauptsatz der Thermodynamik: Einmal erzeugte Entropie kann nur weggeführt und weitergegeben, jedoch nicht vernichtet werden. In einem abgeschlossenen System kann die Entropie niemals abnehmen.
Reversible und irreversible Prozesse

Wenn wir ein heisses Stück Eisen in kaltes Wasser eintauchen, dann wird sich das Stück Eisen abkühlen und das Wasser ganz leicht erwärmen.
Was dabei passiert ist ein Transfer von Wärme \(Q\) vom Eisen an das Wasser. Genauso würde ein stark gekühltes Stück Eisen in warmem Wasser Wärme aufnehmen und das Wasser dabei leicht abkühlen.
Wärmetransport geschieht immer vom System höherer Temperatur hin zum System tieferer Temperatur. Wir verstehen das aufgrund des Teilchenmodells, mit welchem wir uns vorstellen können, wie schnelle Teilchen die langsamen Teilchen anstossen und dabei selber abgebremst werden.
Sobald alle Teilchen in etwa die gleiche Geschwindigkeit haben, sind beide Systeme im thermischen Gleichgewicht und haben deshalb die gleiche Temperatur.
“Temperaturunterschiede gleichen sich spontan aus. Stoffe vermischen sich spontan. Wir beobachten jedoch nie den umgekehrten Vorgang, obwohl er möglich wäre!”
Obwohl er nicht ausgeschlossen ist, beobachten wir den umgekehrten Vorgang niemals. Es sind sog. irreversible Prozesse, d.h. einmal vollzogen, kehrt der Vorgang nicht zurück. Das Wasser wird seine Temperatur behalten und nie mehr sich abkühlen und damit das Stück Eisen erwärmen!
Warum eigentlich nicht? Solange wir dem Wasser gleich viel Energie entnehmen, wie wir dem Stück Eisen zuführen, haben wir den Ersten Hauptsatz der Thermodynamik (Energieerhaltung) erfüllt.
Das Problem liegt aber nicht bei der Energie, sondern bei der Unwahrscheinlichkeit eines solchen Prozesses.
Im Zusammenhang mit Wärme und Vermischungen haben wir es mit Teilchenbewegung zu tun, die in alle möglichen Richtungen zeigen. Wir nennen das chaotische oder ungerichtete Bewegung, weil alle Richtungen statistisch gesehen gleich häufig vorkommen und es keine bevorzugte Richtung gibt.
Es gibt fast unendlich viele Zustände, die einer Unordnung entsprechen, aber es gibt nur einen Zustand, den wir als Ordnung bezeichnen.
Wenn das System mit zufälligen Bewegungen von einem Zustand zu einem anderen ändert, dann ist die Wahrscheinlichkeit, dass wir uns zu diesem einen Zustand mit Ordnung hin bewegen, extrem unwahrscheinlich, eigentlich unmöglich.
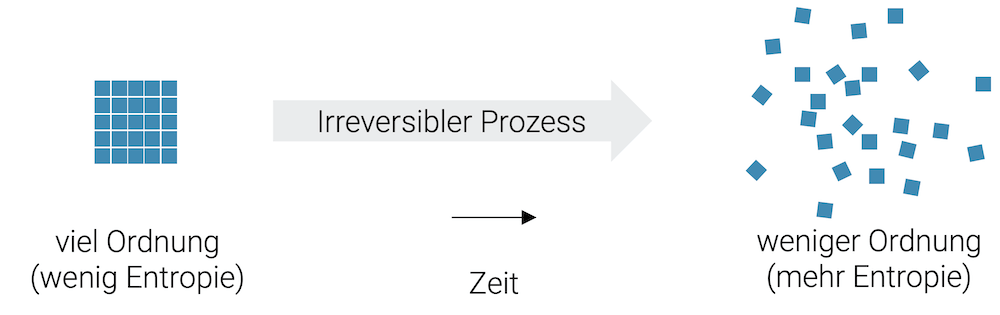
Wenn wir auf einem Tisch viele kleine Würfel schön geordnet aufstellen, haben wir eine Ordnung. Wenn wir aber den Tisch etwas unsanft anstossen, wird diese Ordnung zerstört. Wir haben jetzt Unordnung.
Können wir nicht einfach den Tisch von der anderen Seite zurückstossen und es bildet sich wieder die ursprüngliche Ordnung? Rein theoretisch ist das schon möglich, aber praktisch gesehen, werden wir das nie schaffen.
Alles ist eine Frage der Wahrscheinlichkeit. Hätten wir nur zwei Würfel, könnten wir es uns noch vorstellen, dass sie durch einen sehr geschickten Ruck wieder zusammenkommen und Ordnung wieder zurückkehrt. Je grösser die Anzahl Würfel, desto unwahrscheinlicher wird die Rückkehr zur Ordnung.
Wir haben es mit Teilchenzahlen in der Grössenordnung von Mol, also \(10^23\), zu tun. Die zufällige Rückkehr zu Ordnung kann schlicht ausgeschlossen werden.
Die Zerstörung der Ordnung ist ein irreversibler Prozess, der nicht rückgängig gemacht werden kann.
Ein weiteres Beispiel ist, wenn wir Milchschaum über den schwarzen Kaffee giessen. Nach einer gewissen Zeit haben sich Milch und Kaffee vermischt. Die Vermischung von Milch und Kaffee ist ein irreversibler Prozess bei welchem Ordnung zerstört worden ist.
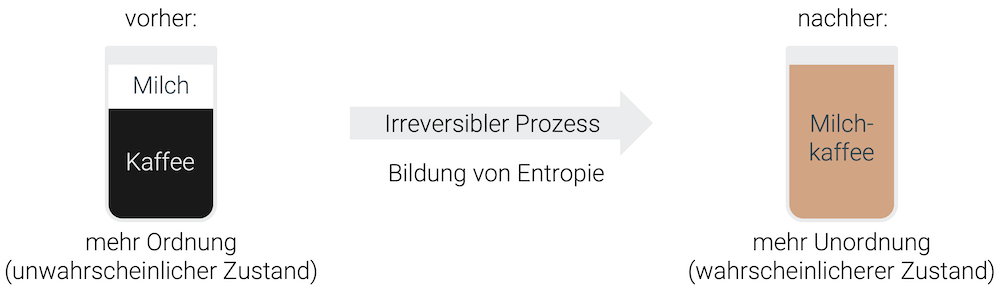

Image by Xavi Cabrera, shared on Unsplash
Entropie
Die Entropie ist eine theoretische Grösse, die von Rudolf Clausius (1822 – 1888) eingeführt wurde. Clausius war ein deutscher Physiker und einer der ersten Professoren an der ETH Zürich. Er gilt als Entdecker des Zweiten Hauptsatzes der Thermodynamik.
Mit der Entropie haben wir eine neue Zustandsgrösse, wie der Druck oder die Temperatur. Sie ist ein Mass der Unordnung oder ein Mass für die Wahrscheinlichkeit eines Zustands.
Je mehr Ordnung wir haben, desto kleiner ist die Entropie bzw. je mehr Unordnung herrscht, desto grösser ist die Entropie. Bei den eben besprochenen Beispielen von irreversiblen Prozessen sind wir von einem Zustand grösserer Ordnung zu einem Zustand grösserer Unordnung gegangen.
Aus Sicht der Entropie ging der Prozess von wenig Entropie hin zu mehr Entropie. Mit dem Zweiten Hauptsatz hielt Clausius fest, dass die Entropie eine Grösse ist, die zunehmen kann, aber niemals spontan abnehmen wird.
Die Entropie ist keine Erhaltungsgrösse, sondern sie kann erzeugt werden.
Zweiter Hauptsatz der Thermodynamik: Einmal erzeugte Entropie kann nur weggeführt, jedoch nicht vernichtet werden. Die Entropie ist eine Grösse, die nur zunehmen kann.
Perpetuum Mobile zweiter Art
Unmögliche Maschinen, die den Ersten Hauptsatz der Thermodynamik (Energieerhaltung) verletzen, nennen wir Perpetuum Mobile, weil sie unendlich lange laufen und dabei noch Energie abgeben.
Jetzt gibt es auch unmögliche Maschinen, die zwar den Ersten Hauptsatz erfüllen, jedoch den Zweiten Hauptsatz verletzen. Diese nennen wir Perpetuum Mobile zweiter Art.
Da der Zweite Hauptsatz schwieriger zu verstehen ist, ist auch die Unmöglichkeit einer solchen Maschine schwieriger erkennbar.
Meistens liegt diesen Maschinen eine irrende Annahme zu Grunde, die letztendlich der Vernichtung von Entropie gleichkommt.
Richtung der Zeit
Angenommen wir würden einen Film anschauen, auf welchem wir den aktuellen Stand der Entropie eines abgeschlossenen Systems sehen könnten: Der Zähler würde immerzu zunehmen, oder?
Sobald wir sehen, dass die Entropie abnimmt (und wir ausschliessen können, dass sie irgendwohin weggeführt worden ist), wissen wir, dass der Film rückwärts geht.
Ohne diese Angabe der Entropie können wir aber bei den meisten physikalischen Prozessen die Zeit einfach umkehren. Fast alle (idealen) Prozesse sind reversibel. In der Strahlenoptik können wir zum Beispiel einen Lichtstrahl vorwärts oder rückwärts laufen lassen; der Weg bleibt der Gleiche.
Es gibt aber auch Prozesse, die offensichtlich irreversibel sind, d.h. in welchen wir sofort erkennen, ob der Film rückwärts läuft oder nicht.
Wenn z.B. eine Tasse herunterfällt und am Boden zu Bruch geht, wissen wir, dass das die normale Laufrichtung des Films ist. Wenn die Bruchstücke sich wieder zu einer Tasse zusammenfinden, dann wissen wir auch sofort, dass das ein rückwärts laufender Film ist.
Die irreversiblen Prozesse geben der Zeit eine klare Richtung. Mit dem Zweiten Hauptsatz der Thermodynamik und der Entropie haben wir der Zeit eine Richtung gegeben!
Dann gibt es noch eine weitere Überlegung: Wenn die Entropie nur zunehmen kann, dann war sie irgendwann einmal null, d.h. einmal war das ganze Universum im Zustand der höchsten Ordnung. Das war der Urknall!
Exergie und Anergie
Wenn wir unser Wissen über reversible und irreversible Prozesse auf die Wärmekraftmaschine anwenden, werden wir sehen, dass sie ein irreversibler Prozess darstellt.
Schauen wir uns aber zuerst reversible Maschinen an: Ein Elektromotor wandelt elektrische Arbeit in mechanische Arbeit um. Ein solcher Prozess ist reversibel. Klar entstehen in realen Maschinen immer kleine Verluste z.B. durch Reibung (irreversibler Prozess). Der grösste Teil der Energie wieder aber reversibel in eine andere Form umgewandelt.

Wir können dann die mechanische Arbeit nehmen und sie in einem Generator wieder zu elektrischer Arbeit zurückverwandeln. Damit ist, bis auf kleinere Verluste, der ursprüngliche Zustand wiederhergestellt, was die Reversibilität gewissermassen beweist.
Schauen wir uns jetzt die Wärmekraftmaschine an. Sie wandelt Wärme in Arbeit und Abwärme um.
Wie viel Arbeit sie maximal gewinnen kann, ist mit dem Carnot-Wirkungsgrad \(\eta_C\) festgelegt.
Angenommen, wir hätten Wärme bei \(T_H=429\;\mathrm{K}\) zur Verfügung und würden die Abwärme bei \(T_K=300\;\mathrm{K}\) an die Umgebung abgeben. Der Carnot-Wirkungsgrad beträgt demnach:
\[ \eta_C = 1 – \frac{300\;\mathrm{K}}{429\;\mathrm{K}} = 1 – 0.7 = 0.3 \]
Wir können im besten Fall 30% der aufgenommenen Wärme in Form von Arbeit umwandeln. Der Rest (70%) muss als Abwärme an die Umwelt abgegeben werden.
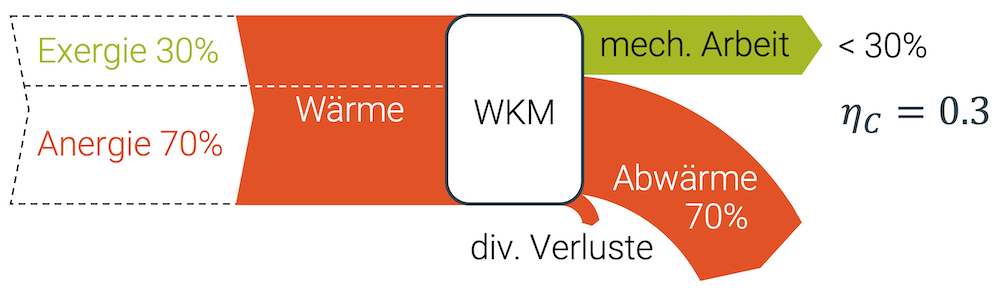
Wenn wir also mit 100% mechanischer Arbeit starten würden, können wir sie zu 100% Wärme umwandeln. Dann gäbe es aber keinen Weg zurück zu den 100% mechanische Arbeit, denn wir könnten allerhöchstens 30% wiederherstellen. Die restlichen 70% sind und bleiben Wärme – für immer!
Aus diesem Grund wird die Wärme auch als eine “weniger edle” Form von Energie angesehen, weil ein Teil der Wärme nicht mehr umwandelbar ist. Wir unterscheiden deshalb:
- Exergie ist der “edle Teil” der Energie, der unlimitiert in andere Energieformen umgewandelt werden kann. Exergie ist nutzbare Energie.
- Anergie ist der “unedle Teil” der Wärme, der nicht mehr in andere Formen umgewandelt werden kann. Anergie ist nutzlose (Ab-)Wärme.
Die edlen Formen von Energie, wie die elektrische und die mechanische Arbeit, bestehen zu 100% aus Exergie und können deshalb zu 100% reversibel umgewandelt werden. Wärme besteht immer als einem Teil Exergie und einem Teil Anergie.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.