Inhalt
Das Wichtigste in Kürze
Bei adiabatischen Zustandsänderungen wird keine Wärme ausgetauscht.
\[ Q=0 \]
Es ändern sich Temperatur, Druck und Volumen gleichzeitig.
Bei einer adiabatischen Kompression nimmt der Druck schneller zu, als bei einer isothermen Kompression, d.h. die Adiabate ist steiler als die Isotherme im \(p,V\)-Diagramm.
Wir haben adiabatische Prozesse, wenn das betrachtete System wärmeisoliert ist oder wenn die Zustandsänderung so schnell stattfindet, dass noch keine nennenswerte Wärme ausgetauscht worden ist, z.B. bei der adiabatischen Kompression der angesaugten Luft im Diesel-Motor.
\[ p_2 = p_1 \cdot \Big(\frac{V_1}{V_2}\Big)^\kappa \]
\[ T_2 = T_1 \cdot \Big(\frac{V_1}{V_2}\Big)^{\kappa – 1} \]
\[ T_2 = T_1 \cdot \Big(\frac{p_1}{p_2}\Big)^{\frac{1-\kappa}{\kappa}} \]
Dabei ist \(\kappa\) der sog. Adiabatenexponent (Isentropenexponent), eine Stoffgrösse, die dem Verhältnis der beiden molaren Wärmekapazitäten bei konstantem Druck \(c_p\) und bei konstantem Volumen \(c_v\) entspricht:
\[ \kappa = \frac{c_p}{c_v} > 1 \]
Videos
Häufigste Fragen
Adiabatische Zustandsänderung
Die adiabatische Zustandsänderung ist dadurch definiert, dass bei ihr keinerlei Wärme ausgetauscht wird:
- Das betrachtete System nimmt keine Wärme auf, bzw.
- das betrachtete System gibt keine Wärme ab.
Ein System kann ja Energie in Form von Arbeit \(W\) aufnehmen oder abgeben, oder in Form von Wärme \(Q\). Im Fall einer adiabatischen Zustandsänderung gilt:
\[ Q = 0 \]
Eine solche Zustandsänderung ist nur theoretisch möglich, da das Fluid sofort Wärme mit seiner Umgebung austauschen kann, insbesondere mit den Wänden seines “Behälters”.
Näherungsweise können aber Zustandsänderungen, die relativ schnell stattfinden, als adiabatisch betrachtet werden. Das Fluid hat nicht genug Zeit um signifikante Mengen von Wärme auszutauschen.
Wenn der Behälter sehr gut wärmeisolierend ist, dann ist die ausgetauschte Wärme vernachlässigbar klein.
Adiabatische Kompression
Bei einer adiabatischen Kompression wird das Fluid komprimiert, was natürlich nur mit einer Zufuhr von Arbeit \(W\) möglich ist, d.h. \( W > 0 \).
Da im adiabatischen Fall keine Wärme zu- oder abgeführt wird, muss die innere Energie \(U\) zunehmen und damit auch die Temperatur.
\[ \require{cancel} \Delta U = W + \cancel{Q} \quad \rightarrow \quad \Delta U > 0 \;\; (W>0) \]
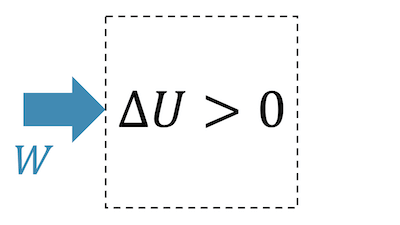
Adiabatische Kompressionen kommen immer dann vor, wenn ein Fluid relativ schnell komprimiert wird, so dass es kaum noch Wärme austauschen kann.
Beispiele für solche adiabatische Zustandsänderungen:
- Schnelles Aufpumpen eines Reifens (Luft im Reifen erwärmt sich)
- Schnelle Verdichtung von Luft in einem Verdichter
- Verdichtung der angesaugten Luft in einem Dieselmotor (Die Luft wird so heiss, dass der eingespritzte Dieseltreibstoff im Kontakt mit ihr verbrennt)
Adiabatische Expansion
Wenn das bereits komprimierte Fluid sich schnell entspannen darf, haben wir den Fall der adiabatischen Expansion. Das Fluid verrichtet Arbeit, d.h. es gibt Arbeit ab: \( W < 0 \).
Wenn das System Energie in Form von Arbeit abgibt, aber keine Energie in Form von Wärme aufnimmt, dann muss die innere Energie \(U\) abnehmen:
\[ \require{cancel} \Delta U = W + \cancel{Q} \quad \rightarrow \quad \Delta U < 0 \;\; (W<0) \]
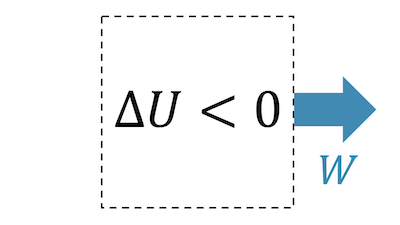
Wenn die innere Energie abnimmt, dann muss auch die Temperatur abnehmen.
Das Gas kühlt sich bei der adiabatischen Expansion ab.
Beispiele für adiabatische Expansion:
- Der Sprühkopf einer Spraydose wird kühl
- Das Fluid in einer Kältemaschine oder Wärmepumpe wird durch adiabatische Expansion in einem Drosselventil entspannt, so dass es sich plötzlich abkühlt
“Die Adiabate ist im p,V-Diagramm eine steilere Kurve als die Isotherme.”
Adiabate im p,V-Diagramm
Eine adiabatische Kompression verläuft im p,V-Diagramm steiler als eine isothermische Kompression, da nicht nur der Druck zunimmt, sondern mit auch die Temperatur. Der Zustandspunkt geht damit zu einer höheren Isothermen.
Die Zustandspunkte, die zu dieser adiabatischen Kompression gehören, liegen auf der Adiabate. Sie ist ähnlich gekrümmt wie eine Isotherme, nur steiler.
Aus \(\Delta U = W\) folgt für die adiabatische Zustandsänderung:
\[ p_1 \cdot V_1^\kappa = p_2 \cdot V_2^\kappa \]
\[ p_2 = p_1 \cdot \Big(\frac{V_1}{V_2}\Big)^\kappa \]
Für die Herleitung sei auf den Artikel in Wikipedia verwiesen: Adiabatische Zustandsänderung (Wikipedia)
Der Adiabatenexponent \(\kappa\) ist eine stoffabhängige Grösse, die dem Verhältnis der spezifischen Wärmekapazitäten \(c_p\) und \(c_v\) entspricht. Manchmal wird diese Grösse auch Isentropenexponent genannt.
\[ \kappa = \frac{c_p}{c_v} \]
Die Grösse \(c_p\) ist die molare Wärmekapazität bei konstantem Druck und analog steht \(c_v\) für die molare Wärmekapazität bei konstantem Volumen. Für Luft haben wir einen Adiabatenexponenten von \(\kappa = 1.4\).
Aus der ersten Gleichung (oben) erhalten wir für die Adiabate:
\[ p \cdot V^\kappa = \text{konstant} \]
Leicht umgeformt, erhalten wir:
\[ p(V) = C \cdot \Big(\frac{1}{V}\Big)^{\kappa} \]
Im \(p,V\)-Diagramm wäre das eine Hyperbel-Funktion. Für die isothermische Zustandsänderung hatten wir beim Gesetz von Boyle-Mariotte:
\[ p \cdot V = \text{konstant} \quad \rightarrow \quad p(V) = C \cdot \Big(\frac{1}{V}\Big) \]
Im adiabatischen Fall kommt aber ein Exponent \(\kappa\) hinzu, der grösser als eins ist \((\kappa > 1)\). Die Funktion verläuft wie eine Hyperbel, nur etwas steiler.
Mit der idealen Gasgleichung erhalten wir für die adiabatische Zustandsänderung noch die folgenden Formeln:
\[ T_2 = T_1 \cdot \Big(\frac{V_1}{V_2}\Big)^{\kappa – 1} \]
\[ T_2 = T_1 \cdot \Big(\frac{p_1}{p_2}\Big)^{\frac{1-\kappa}{\kappa}} \]
Beispiel
Beispiel
Aufgabensammlung
Lernziele
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.