Wärmeleitung

Mechanismen der Wärmeleitung

Die Wärmeleitung ist die Übertragung der Wärmebewegungen von einem Bereich mit stärkerer Bewegung (höherer Temperatur) auf einen Bereich mit schwächerer Bewegung (niedrigerer Temperatur). Wenn die beiden Bereiche in Kontakt sind, können die Bewegungen vom einen Bereich auf den anderen übertragen werden. Damit haben wir bereits die beiden Voraussetzungen für die Wärmeleitung:

• Es braucht eine Temperaturdifferenz
• Die beiden Bereiche müssen in physischem Kontakt stehen, d.h. sich berühren.

Wenn wir einen Feststoff z.B. am einen Ende erwärmen, dann werden die Teilchen in stärkere Bewegung gebracht. Da sie über Bindungskräfte mit dem restlichen Kristallgitter verbunden sind, überträgt sich diese zusätzliche Bewegung an den Nachbarn und von diesem wieder an seinen Nachbarn usw. Wir sprechen da von Übertragung der Gitterschwingungen. In der Feststoffphysik werden die Gitterschwingungen als virtuelle Teilchen modelliert, den Phononen. Die entstandenen Phononen wandern im Feststoff und erhöhen so die Temperatur allmählich auch am kalten Ende. Dieser Mechanismus gibt es grundsätzlich in allen Stoffen.

Metalle haben die Eigenschaft, dass sie freie Elektronen haben. Das ist der Grund für die hervorragende elektrische Leitfähigkeit von Metallen. Nun können Elektronen, wie die Phononen, Wärme übertragen. Metalle unterscheiden sich deshalb auch in der Wärmeleitung von isolierenden Stoffen wie Holz oder Kunststoff. Sie leiten die Wärme besonders gut, da die Elektronen sehr effiziente Wärmetransporteure sind.

Wenn wir ein Metall berühren, dann fühlt es sich meistens kühl an. Bei der Besprechung des Unterschieds zwischen Wärme und Temperatur haben wir gelernt, dass unsere Rezeptoren in der Haut eigentlich die Wärme und nicht die Temperatur messen. Das Metall fühlt sich kühl an, weil durch die grosse Wärmeleitung (wegen der Elektronen), die Haut am Metall mehr Wärme abgibt als z.B. beim Berühren von Holz.

Wenn wir mit Wärmeleitung effizient kühlen (oder heizen) möchten, dann benutzen wir vorzugsweise Metall. Ein thermischer Motor muss stark gekühlt werden. Er hat deshalb viele Kühlrippen aus Metall, die die Wärme aus dem Inneren des Motorblocks an die Oberfläche mit Wärmeleitung transportieren. Dort wird die Wärme an den Fahrtwind, also an die vorbeiströmende Luft abgegeben.

Wenn wir den Wärmestrom möglichst unterbinden, d.h. die Wärme isolieren möchten, dann eignen sich elektrisch isolierende Stoffe, allen voran Gase. In Gasen gibt es nämlich keine Phononen (keine Gitterschwingungen) und auch keine freien Elektronen (nur gebundene Elektronen).

Die Wärme kann nur durch die einzelnen Teilchen transportiert werden, was aber nicht sehr effizient ist, da wir eine viel kleinere Teilchendichte haben als im Falle von Festkörpern oder Flüssigkeiten, d.h. es gibt rund tausend mal weniger Teilchen, die bereit sind, Wärme zu transportieren.

Ein Problem gibt es mit Gasen: Sie können mit Konvektion Wärme transportieren. Um dies zu verhindern, müssen die Gase in kleinen Zwischenräumen eingeschlossen werden. Das verhindert den Wärmetransport durch Konvektion. Die Natur macht es vor: Dicke Schafswolle ist eigentlich in erster Linie eingeschlossene Luft, die nicht fliessen kann. Dadurch kann die Körperwärme nur über diese eingeschlossene Luft nach aussen transportiert werden und das geht sehr schlecht. Resultat: Der Körper verliert fast keine Wärme.

Temperaturgradient als treibender Faktor

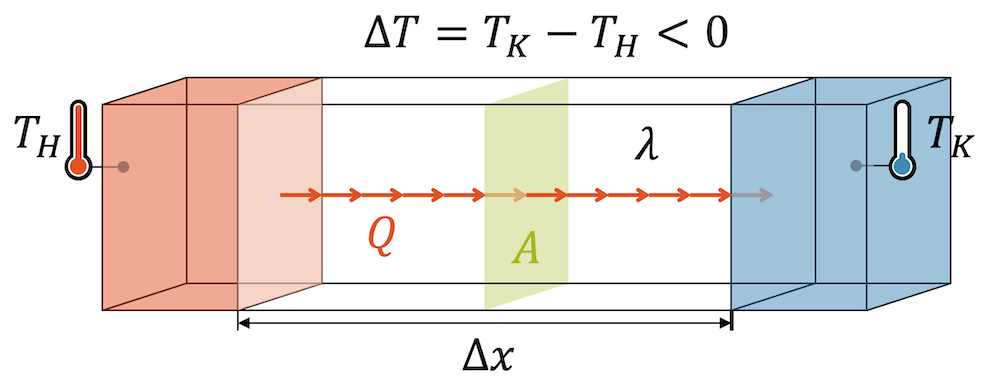
Wenn zwei Körper mit unterschiedlichen Temperaturen miteinander in Kontakt stehen, dann haben wir die Voraussetzungen für die Wärmeleitung erfüllt. Wie viel Wärme fliesst, hängt aber auch davon ab, wie gross der Abstand zwischen den beiden Temperaturextremen ist. Wir können uns das so vorstellen, dass bei einem kleinen Abstand, der Temperaturunterschied gewissermassen “dringender” ist, als bei einem grossen Abstand. Diese “Dringlichkeit” wird mit dem Temperaturgradienten \(\frac{\Delta T}{\Delta x}\) beschrieben.

Nebst der Temperaturdifferenz \(\Delta T\) beinhaltet der Temperaturgradient auch den Abstand \(\Delta x\). Die Formel des Temperaturgradienten erinnert uns an das Steigungsdreieck. Es ist die Zunahme der Temperatur pro Strecke. Je stärker die Temperatur pro Strecke zunimmt, desto grösser ist der Temperaturgradient. Ein negativer Temperaturgradient entspricht einer Temperaturabnahme über die Strecke \(\Delta x\).

Die Temperaturdifferenz ist die Voraussetzung für die Wärmeleitung überhaupt, der Temperaturgradient sagt aber, wie viel Wärme fliesst. Da die Wärme vom Ort der höheren Temperatur \(T_H\) (heiss) zum Ort der tieferen Temperatur \(T_K\) (kalt) fliesst, wird der negative Temperaturgradient in der Formel benutzt, da \(\Delta T = T_K – T_H\) negativ ist. Damit ist der negative Temperaturgradient wieder positiv:

\[ \Delta T = T_K – T_H < 0 \quad \rightarrow \quad \Big( – \frac{\Delta T}{\Delta x} \Big) > 0 \]

Er ist der treibende Faktor für den Wärmestrom. Der Wärmestrom ist Energie pro Zeit. Für den Wärmestrom schreiben wir deshalb: \(\frac{\Delta Q}{\Delta t}\).

Der Wärmestrom \(\frac{\Delta Q}{\Delta t}\), der durch Wärmeleitung fliesst, beträgt:

\[ \frac{\Delta Q}{\Delta t} = \lambda \cdot A \cdot \Big( – \frac{\Delta T}{\Delta x} \Big) \]

Der Wärmestrom ist natürlich umso grösser, je grösser der Temperaturgradient ist. Der Wärmestrom hängt auch von der Querschnittsfläche \(A\) ab. Sie ist die Grösse der Kontaktfläche und ist somit die Grösse des “Tors” durch welches die Wärme fliesst. Die Wärmeleitungseigenschaften des Materials werden mit dem Wärmeleitungskoeffizienten \(\lambda\) berücksichtigt.

Aus der obigen Formel leiten wir ab, dass wir einen grossen Wärmestrom durch Wärmeleitung haben, bei:

• gut leitendem Stoff mit grossem Wärmeleitungskoeffizienten \(\lambda\)
• grosser Querschnittsfläche \(A\) (quer zur Fliessrichtung)
• grossem Temperaturgradienten \(\big( – \frac{\Delta T}{\Delta x} \big)\), d.h. \(|\Delta T|\) gross, \(\Delta x\) klein

Mit einer möglichst dicken Glasscheibe verkleinert sich der Temperaturgradient, der treibende Faktor bei der Wärmeleitung!

\[ \frac{\Delta -T}{\Delta x} \]

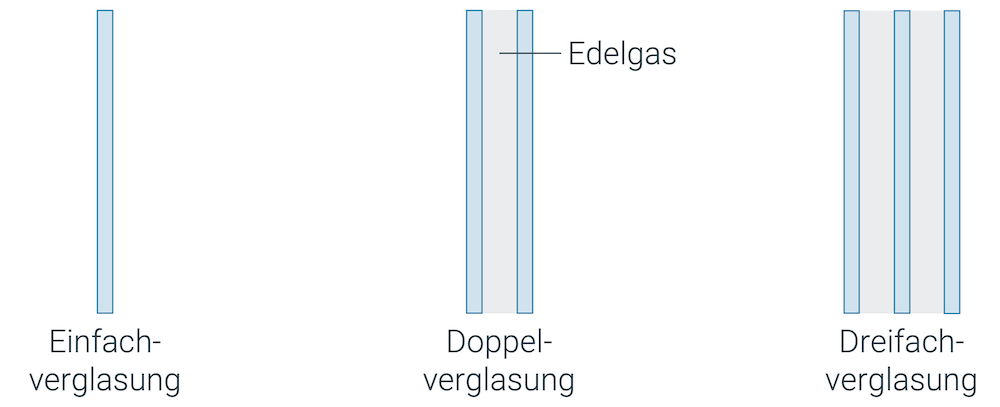
Wir möchten aber nicht die Dicke der Glasscheibe vergrössern, sondern die Dicke des Fensters insgesamt. Das machen wir am besten, indem wir einen möglichst grossen Zwischenraum zwischen den Scheiben haben.

Wir müssen ein Gas einfüllen, denn sonst hätten wir den Druck zwischen aussen (Luft) und innen (Vakuum) nicht ausgeglichen und der Luftdruck würde die beiden Glasscheiben eindrücken.

Mit dem eingefüllten Gas handeln wir uns aber gleich wieder ein anderes Problem ein: Das Gas kann sich auf der einen Seite erwärmen und zur kalten Seite fliessen. Diese natürliche Konvektion ist wieder eine Art Wärmetransport, den wir zu verhindern versuchen.

Deshalb wird eine dritte Scheibe in die Mitte gesetzt, um diese Konvektion von der kalten Scheibe zur warmen Scheibe zu verhindern.

Fertig ist die Dreifachverglasung, die heutzutage die best-isolierenden Fenster macht!