Spezifische Wärmekapazität

Temperaturzunahme bei Wärmezufuhr

Wir können uns konzeptionell vorstellen, dass sich die Temperatur erhöht, wenn wir einem Stoff Wärme zuführen. Mehr thermische Energie bedeutet ja auch schnellere Teilchenbewegung.

Wie sind jedoch die Grössen Temperatur \(T\) und Wärme \(Q\) mit einander verknüpft? Wie können wir berechnen, um wie viele Grad sich ein Stoff erwärmt, wenn wir z.B. 1 kJ Wärme zuführen?

Aus Experimenten fand man heraus, dass die Energiemenge und die Temperaturänderung eine lineare Abhängigkeit von einander haben, d.h. wenn wir die doppelte Menge an Wärme zuführen, ist die Temperaturänderung ebenfalls doppelt so gross.

\[ Q = m \cdot c \cdot \Delta T \quad \rightarrow \quad \Delta T = \frac{Q}{(m \cdot c)} \]

Je mehr Masse \(m\) wir haben, desto mehr Wärme können wir dem Stoff geben, bis er mit einer bestimmten Temperaturänderung reagiert.

Schliesslich haben wir in der Gleichung die Stoffgrösse, die spezifische Wärmekapazität \(c\). Sie berücksichtigt die Eigenschaften des betreffenden Stoffs, wenn es um Speicherung von thermischer Energie geht.

Die spezifische Wärmekapazität \(c\) ist die Wärmekapazität eines Stoffs pro Kilogramm.

Je grösser diese ist, desto kleiner wird die Temperaturänderung sein, denn die Energie lässt sich dank der grossen Kapazität “leicht verstauen”.

Stoffe mit kleiner Wärmekapazität reagieren auf eine Wärmezu- oder abfuhr mit einer starken Zu- bzw. Abnahme der Temperatur.

Beachte, dass die spezifische Wärmekapazität keine reine Stoffgrösse ist, sondern selber auch von der Temperatur abhängig ist. Bei nicht zu grossen Temperaturänderungen können wir dies vernachlässigen und einfach mit einem konstanten Wert rechnen.

Wir nehmen z.B. den Wert der spezifischen Wärmekapazität aus einer Tabelle, die aber streng genommen nur für die Temperatur von 25 °C gilt und berechnen eine Erwärmung auf 100 °C. Das ist genug genau. Wenn wir jedoch auf 1000 °C heizen oder auf -200 °C abkühlen würden, müsste die spezifische Wärmekapazität unterwegs angepasst werden.

Definitionen

Abkürzung: \(c\)

Einheit: \([\,c\,] = \frac{\text{J}}{\text{kg K}}\)

Beachte, dass für Gase die folgenden zwei spezifischen Wärmekapazitäten unterschieden werden, da sich Gas stark ausdehnen oder komprimieren lassen:

• \(c_V\) ist spezifische Wärmekapazität bei konstant gehaltenem Volumen \(V\)
• \(c_p\) steht für die spezifische Wärmekapazität bei konstant gehaltenem Druck \(p\)

Bei konstant gehaltenem Volumen kann das Gas keine Arbeit verrichten, so dass sämtliche Wärme \(Q\) in der inneren Energie des Gases gespeichert wird. Bei konstant gehaltenem Druck, expandiert das Gas durch die Wärmezufuhr \(Q\) und die innere Energie nimmt zwar zu, wird aber um den Betrag der Expansionsarbeit \(W\) reduziert.

Wenn die innere Energie weniger stark zunimmt, nimmt auch die Temperatur weniger stark zu, d.h. bei gleicher Wärmezufuhr haben wir eine kleinere Temperaturerhöhung. Das macht, dass \(c_p > c_V\), jedoch für den gleichen Stoff. Wir müssen hier also den Prozess, entweder isochor (\(V\) konstant) oder isobar (\(p\) konstant) unterscheiden.

Wir haben die Stoffmenge mit der Masse beschrieben und deshalb die spezifische Wärmekapazität als die Wärmekapazität pro Kilogramm definiert.

In der Chemie ist oft die Definition pro Mol üblich: Es ist die molare Wärmekapazität \(C_m\). Wenn wir eine bestimmte Stoffmenge betrachten, dann können wir die absolute Wärmekapazität schreiben als \((m \cdot c)\) oder eben auch als \((n \cdot C_m)\), wobei \(n\) die Anzahl \(\text{mol}\) ist, also ein Mass für die Anzahl Teilchen:

\[ (m \cdot c) = (n \cdot C_m) \]

Mit der molaren Masse \(M = \frac{m}{n}\), also der Masse pro Mol, erhalten wir eine Umrechnung von der spezifischen Wärmekapazität \(c\) zur molaren Wärmekapazität \(C_m\) bzw. umgekehrt:

\[ C_m = \frac{m}{n} \cdot c = M \cdot c \]

Experimentelle Bestimmung der spezifischen Wärmekapazität

Es gibt ein relativ einfaches Experiment für die Bestimmung der spezifischen Wärmekapazität \(c\).

Mit einem elektrischen Heizdraht lässt sich die elektrische Leistung \(P\) einfach und genau bestimmen. Wir wissen somit, wie viel Energie pro Zeit in den zu untersuchenden Stoff geleitet wird.

Wir müssen aber beachten, dass die zugeführte Energie nicht wieder an die Umgebung abgegeben wird, sondern für die Erwärmung unseres Stoffs benötigt wird. Dazu wird ein sog. Kalorimeter benutzt, ein Gefäss, dass wärmeisolierend ist, wie ein Thermoskrug.

Wir führen eine gewisse Zeit \(\Delta t\) lang Energie zu mit einer bekannten elektrischen Leistung \(P\), d.h. 

\[ P = \frac{\Delta E}{\Delta t} \quad \rightarrow \quad \Delta E = Q = P \cdot \Delta t \]

Somit kennen wir die zugeführte Wärme \(Q\). Die Masse \(m\) wurde vorgängig gemessen, d.h. jetzt fehlt nur noch die Temperaturänderung \(\Delta T\) und wir können die spezifische Wärmekapazität \(c\) berechnen:

\[ Q = m \cdot c \cdot \Delta T \quad \rightarrow \quad c = \frac{Q}{m\;\Delta T} \]

Genauer wird es, wenn wir über eine gewisse Zeit lang aufheizen und die Messpunkte in einem \(T,Q\)-Diagramm auftragen, d.h. ein Temperaturverlauf als Funktion der zugeführten Wärme \(Q\). Die Messpunkte bilden eine Gerade mit einer bestimmten Steigung, also eine lineare Funktion.

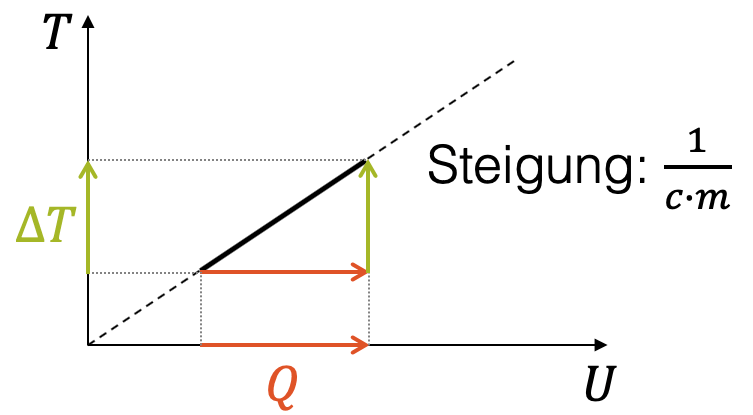
Im \(x,y\)-Koordinatensystem wäre das \(y(x)=a \cdot x\) mit der Steigung \(a\). Hier haben wir \(T(Q)=a \cdot Q\). Für die Steigung der Geraden gilt:

\[ Q = m \cdot c \cdot \Delta T \quad \rightarrow \quad a = \frac{\Delta T}{Q} = \frac{1}{c \cdot m} \]

Die Steigung ist umgekehrt proportional zum Produkt von Masse und spezifischer Wärmekapazität \((m \cdot c)\).

Wenn wir einen Stoff mit einer grossen Wärmekapazität \((m \cdot c)\) haben, wird die Temperatur nur leicht steigen. Die zugeführte Wärme \(Q\) kann sich auf eine grosse Masse verteilen und diese Masse hat zudem eine grosse Kapazität und kann viel Energie speichern.

Stell Dir vor, du würdest das Wasser eines Swimmingpools mit einem kleinen Wasserkocher zu erwärmen versuchen. Die Temperatur würde kaum steigen.

Anders herum, steigt bei einer sehr kleinen Wärmekapazität \((m \cdot c)\) die Temperatur sehr schnell an, weil die zugeführte Wärme \(Q\) auf wenig Masse \(m\) und auf einen Stoff mit kleiner spezifischer Wärmekapazität \(c\) trifft.

Wohin mit der Wärme? Es gibt beschränkt viele Teilchen und die können nicht viel anfangen mit der Energie, also wird ihre Bewegung einfach schneller und wir erreichen in Kürze eine hohe Temperatur.

Freiheitsgrade

Translatorische Freiheitsgrade

Wir haben bisher nicht genauer untersucht, wie es sein kann, dass gewisse Stoffe mehr Energie speichern können als andere. Es gibt dazu viele Gründe, aber einer liegt in der Anzahl Freiheitsgrade begründet.

Gase können im Teilchenmodell als einzeln fliegende Teilchen modelliert werden. Ihre thermische Energie finden wir in der kinetischen Energie dieser Teilchen, denn sie fliegen mit grosser Geschwindigkeit und haben ja eine Masse, d.h. \(E_{kin} = \frac{1}{2}m v^2\)

Ein einatomiges Gas, z.B. das Edelgas Argon, kann so modelliert werden. Wir sagen auch, dass die Teilchen drei Freiheitsgrade haben, denn sie können sich in \(x\)-, in \(y\)- und in \(z\)-Richtung bewegen bzw. in allen erdenklichen Kombinationen dieser drei Richtungen. Mit anderen Worten: Sie können sich im dreidimensionalen Raum bewegen. Wir nennen diese Bewegungen die translatorischen (geraden) Bewegungen oder “Verschiebungen”.

Rotative Freiheitsgrade

Jetzt gibt es aber Gase, die mehr Freiheitsgrade haben, als Argon. Sauerstoff \(O_\text{2}\) und Stickstoff \(N_\text{2}\) bestehen aus jeweils zwei Atomen. Wir können sie als starre Hanteln uns vorstellen. Nun können Hanteln, genauso wie Kugeln, beliebig im dreidimensionalen Raum herumfliegen. Zusätzlich kennen sie aber auch die Rotation.

Wenn wir die die starre Hantel im dreidimensionalen Raum in die \(y\)-Achse legen, dann kann sie um die \(x\)-Achse rotieren oder auch um die \(z\)-Achse. Die zwei neuen Freiheitsgrade erlauben ein zusätzliches Speichern von Energie, denn es gibt ja die Rotationsenergie: \(E_{rot} = \frac{1}{2} I \omega^2\)

Was ist mit dem Rotieren um die \(y\)-Achse? Grundsätzlich ist eine solche Rotation denkbar, allerdings ist das Trägheitsmoment \(I\) so klein, dass diese Rotationsenergie kaum ins Gewicht fallen würde.

Auch würde sich die Frage stellen, was das denn heisst, wenn ein Atom um seine eigene Achse dreht? Meinen wir dann die Rotation der Bestandteile des Atoms – die Elektronen? Die haben fast keine Masse! Die Masse liegt im Kern des Atoms und der ist ja \(10^5\)-fach kleiner als das Atom!

Die Rotation des Atomkerns um seine eigene Achse, wenn überhaupt, können wir definitiv vernachlässigen! Wir merken uns deshalb, dass nur die Rotationen einer zweiatomigen Hantel quer zur Hantelachse zählen. Deshalb gibt es zwei und nicht drei zusätzliche Freiheitsgrade für die Rotation.

Bei mehr-atomigen Molekülen, die von allen Seiten gesehen grösser sind als nur ein Atom, können wir drei zusätzliche Freiheitsgrade für die Rotation zählen.

Oszillative Freiheitsgrade

Bei höheren Temperaturen kommen bei zweiatomigen Gasen noch weitere Freiheitsgrade hinzu. Die zwei Atome sind aneinander gebunden, können sich aber etwas annähern und wieder entfernen, als wären sie mit einer Feder verbunden. Ihre Bindung verhält sich tatsächlich wie eine Feder, jedoch nicht wie eine mechanische Feder, sondern wie eine Feder mit Coulombkraft.

Auf jeden Fall können die beiden Atome als Paar schwingen (oszillieren). Die Kräfte sind hier recht gross, weshalb es schon viel Energie (und somit Temperatur) braucht, um sie so zum Schwingen zu bringen. Das Schwingen von einer “Feder” zählt als zwei zusätzliche Freiheitsgrade.