Inhalt
Das Wichtigste in Kürze
Die Temperatur beschreibt die Stärke der Bewegung der Teilchen. Temperaturen werden mit Thermometern gemessen. Beim Flüssigkeitsthermometer kann die Volumenausdehnung der gefärbten Flüssigkeit an einer Skala als Temperatur abgelesen werden.
Die Teilchen bewegen sich bei einer bestimmten Temperatur nicht alle gleich schnell: Es gibt immer langsamere und schnellere Teilchen. Dennoch verändert sich die Geschwindigkeitsverteilung mit der Temperatur.
Im Alltag benutzen wir v.a. die Celsius-Skala. In der Wissenschaft wurde diese aber durch die Kelvin-Skala abgelöst, da sie den absoluten Charakter der Temperatur berücksichtigt.
Der absolute Nullpunkt ist der (theoretische) Zustand tiefster Temperatur, nämlich dann, wenn die Teilchen aufhören würden, sich zu bewegen.
Der absolute Temperaturnullpunkt liegt bei -273.15 °C. Da die Schrittlänge in der Celsius- und der Kelvin-Skala gleich lang sind, können wir bei Temperaturdifferenzen die Einheiten einfach umtauschen:
\[ \Delta T = 1\;\text{K} = 1\;^\circ\text{C} \]
Für die absoluten Temperaturen addieren wir zur Zahl in Grad Celsius die Differenz 237.15 hinzu:
\[ T_1 = 0\;\text{K} = -237.15\;^\circ\text{C} \]
\[ T_2 = 273.15\;\text{K} = 0\;^\circ\text{C} \]
Videos
Häufigste Fragen
Definitionen
Abkürzung: \(T\)
Einheit für Temperatur: \([\,T\,] = \text{K}\) (Kelvin)
Einheit für Temperaturdifferenzen: \([\,\Delta T\,] = \text{K}\) (Kelvin) \( = \; ^\circ \text{C}\) (Grad Celsius)
Celsius- und Kelvinskala
Die Thermometer zeigen die Temperatur in Grad Celsius an mit der Abkürzung °C, benannt nach dem schwedischen Astronomen, Anders Celsius (1701 – 1744).
In den USA, Belize und Liberia und ein paar Inselstaaten sind noch die Grad Fahrenheit (°F) in Gebrauch, die hier aber nicht weiter diskutiert werden.
In der Wissenschaft wird die Temperatur mit Kelvin (K) angegeben, benannt nach Lord Kelvin (1824 – 1907) einem irisch-schottischen Physiker und Ingenieur. Beachte, dass man nie “Grad Kelvin” sagt, sondern nur “Kelvin” !
Der Zusammenhang zwischen der Celsius und der Kelvin-Skala ist glücklicherweise sehr einfach.
Beide Skalen sind für die Temperaturdifferenzen \(\Delta T\) gleich, d.h. wenn wir um ein Grad Celsius erwärmen, ist das gleichzeitig auch ein Kelvin wärmer.
Wie im obigen Video benutze ich hier die Analogie zu einem Wolkenkratzer in welchem die Stockwerke mit Grad Celsius und mit Kelvin angeschrieben sind. Wenn wir ein Stockwerk hochgehen, erhöhen sich beide Zahlen um eins. Wenn wir zehn Stockwerk aufsteigen, erhöhen sich beide Zahlen um zehn etc.
| Temperaturdifferenz | Celsius-Skala | Kelvin-Skala |
| \(\Delta T\) | +1 °C | +1 K |
| \(\Delta T\) | +10 °C | +10 K |
| \(\Delta T\) | -100 °C | -100 K |
Absolute Temperaturen \(T\) sind um den Betrag 273.15 verschoben. Auch hier ist die Analogie mit dem Wolkenkratzer hilfreich: Wenn es nicht darum geht, wie viele Stockwerk man hoch oder runter geht, sondern auf welchem Stockwerk man sich effektiv befindet, dann spricht man von einer absoluten Temperatur.
Aus historischen Gründen wurde die Celsiusskala so festgelegt, dass 0 °C dem Schmelzpunkt von Wasser-Eis bei üblichem Umgebungsdruck entspricht. Deshalb gibt es auch Temperaturen unter null. Es ist, als hätten wir den 273. Stock mit null angeschrieben. Alles darunter ist unter null.
Wasser hat für uns eine besondere Bedeutung. Warum wir aber die Skala für die Temperatur an diesem Stoff binden, ist eine willkürliche Wahl.
Die Kelvinskala hat hier einen anderen Anspruch. Sie ist das Mass für die absolute Temperatur, d.h. 0 K entspricht dem absoluten Temperatur-Nullpunkt. Negative Kelvinwerte kann es gar nicht geben.
Unser Wolkenkratzer hat keinen Keller. Wir sind auf dem absoluten Felsen der Physik angelangt!
Ebenfalls merken solltest du dir die Temperatur von 300 K. Diese runde Zahl in Kelvin entspricht sommerlichen (300 – 273.15) °C = 26.85 °C.
| Temperatur | Celsius-Skala | Kelvin-Skala |
| \(T\) | -273.15 °C | 0 K |
| \(T\) | 0 °C | 273.15 K |
| \(T\) | 300 °C | 300 K |
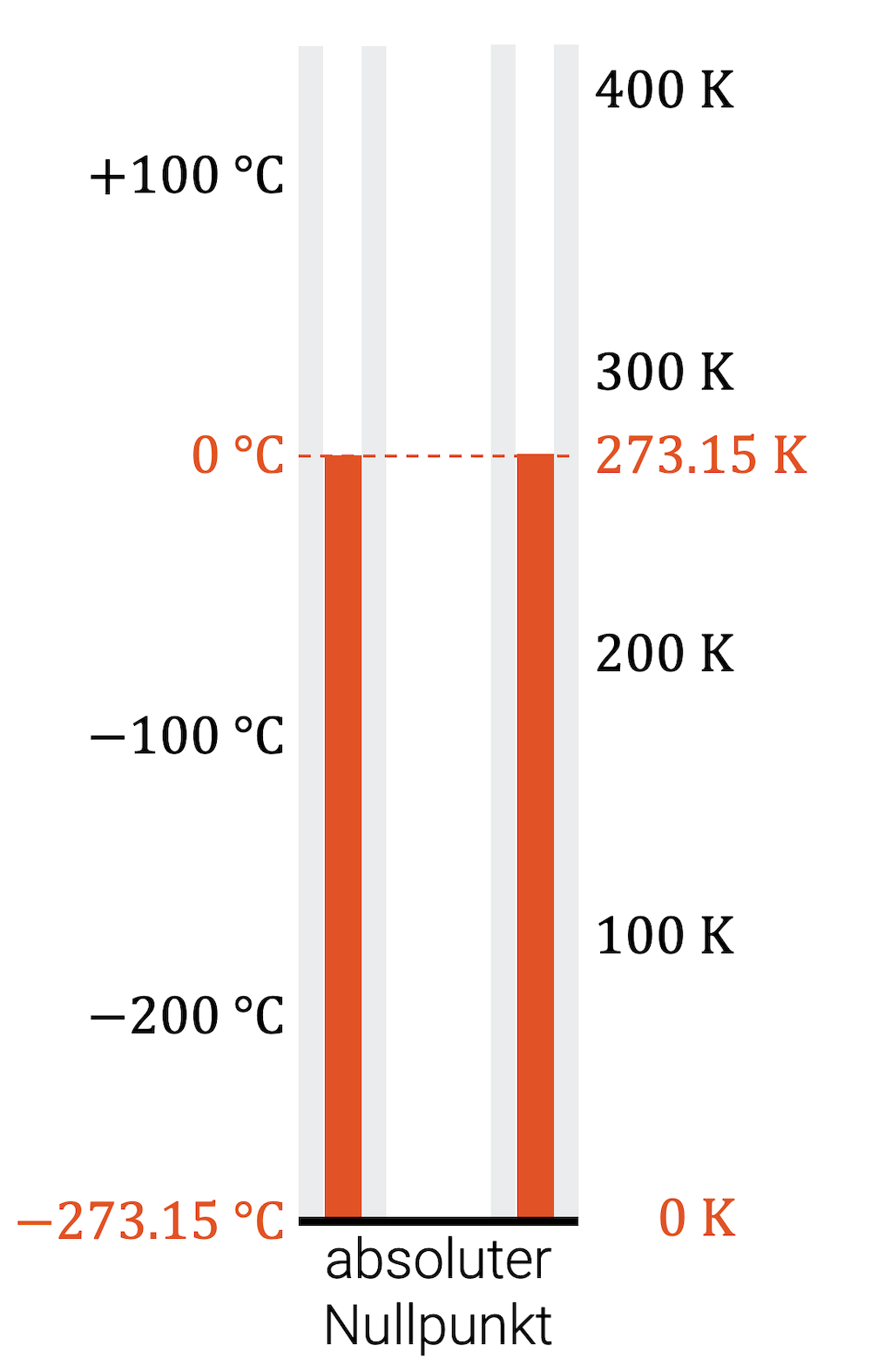
“Teilchen können sich nicht noch langsamer bewegen als gar nicht.”
Warum es einen absoluten Temperaturnullpunkt haben muss
Der französische Erfinder und Wissenschaftler Guillaume Amontons (1663– 1705) vermutete als Erster den absoluten Nullpunkt.
Er machte Experimente mit einer konstanten Menge an Gas, eingeschlossen in einem konstanten Volumen. Dann veränderte er die Temperatur des Gases mit Hilfe von kaltem Wasser bis hin zu kochendem Wasser und bemerkte, dass sich der Gasdruck um rund einen Drittel veränderte.
Er schloss daraus, dass in umgekehrter Richtung, also mit Hilfe einer weiteren Abkühlung, die für ihn nicht durchführbar war, es irgendwann einen Punkt geben müsste, wo der Druck null sein würde.
Was heisst das: “Druck ist null”? Der Druck entsteht durch die Stösse der Teilchen auf die Behälterwand. Wenn der Druck verschwindet, haben wir keine Stösse mehr und das bedeutet, dass die Teilchen sich nicht mehr bewegen.
Teilchen können sich nicht noch langsamer bewegen als gar nicht. Die Nullgrenze ist eine physikalische Grenze, die nicht unterschritten werden kann.
Amontons Temperaturmessungen waren nicht so genau und seine Schätzung war, dass dieser unterste Punkt bei grob \(T = -240\,^\circ\text{C}\) liegen müsste. Dennoch war er dem absoluten Temperaturnullpunkt schon dicht auf der Spur!
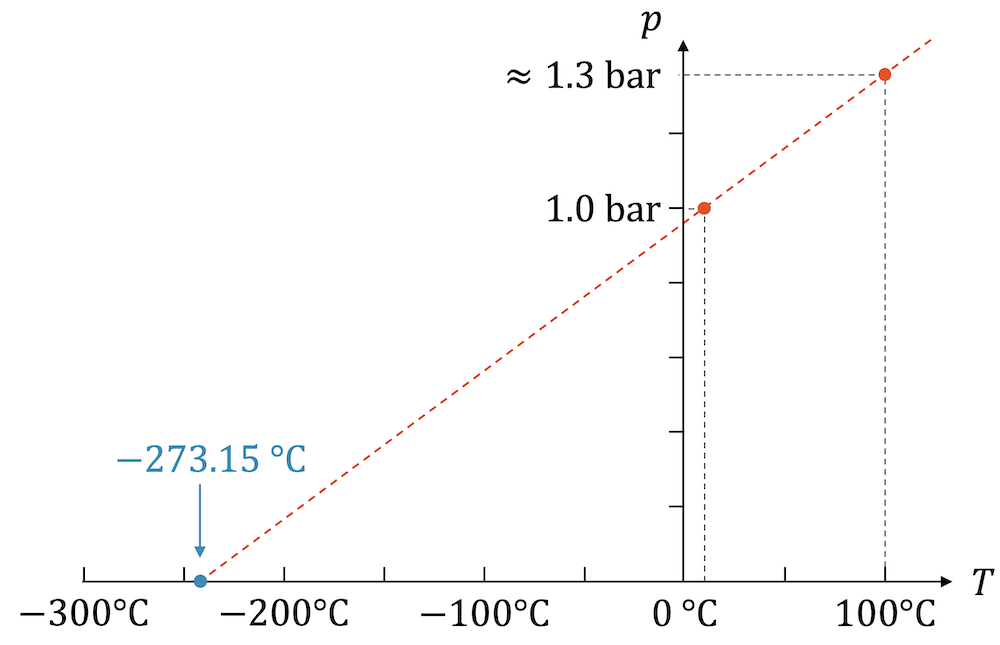
Im nachfolgenden Diagramm ist gezeigt, wie die Messungen auf einer Linie liegen, d.h. die Steigung ist überall gleich.
Wenn wir die Steigung zwischen den beiden Messpunkten ermitteln, erhalten wir:
\[ \frac{\Delta p}{\Delta T} = \frac{0.3\;\text{bar}}{80^\circ\text{C}} \]
Für das grosse Steigungsdreieck muss die Temperaturdifferenz also \(\frac{80\text{°C}}{0.3} = 267^\circ\text{C}\) betragen. Von einer Temperatur von \(20^\circ \text{C}\) nach links abgetragen ergibt das:
\[ 20^\circ \text{C} – 267^\circ \text{C} = -247^\circ \text{C} \]
Bei dieser Temperatur müsste der Druck die unterste Grenze null erreichen.
Ich finde es erstaunlich, dass Ende des 17. Jahrhunderts eine so fundamentale Vermutung gemacht werden konnte. Natürlich konnten diese tiefen Temperaturen nicht erzeugt werden. Die Kältemaschine würde erst 1845 erfunden werden.
Temperatur als Mass für die Teilchenbewegung
Von der Brownschen Bewegung wissen wir, dass Teilchen sich bewegen und sogar so stark, dass sie hundertausendfach grössere Pollenkörner anstossen können.
Wenn wir Diffusionsprozesse beobachten, erkennen wir, dass sie bei höherer Temperatur schneller ablaufen. Die Temperatur ist ein Mass für mittlere Geschwindigkeit der Teilchen.
Das Flüssigkeitsthermometer selbst nutzt die Teilchenbewegung aus. Je schneller die Teilchen, desto mehr Platz brauchen sie: Die Flüssigkeit dehnt sich leicht aus (Wärmeausdehnung) und wir sehen das am Steigen der Flüssigkeitssäule.

Ist das nicht unglaublich? Wir können die Teilchen zwar nicht sehen, weil sie unglaublich klein sind. Wir können indirekt aber ihre mittlere Geschwindigkeit mit einem einfachen Flüssigkeitsthermometer messen!
Warum “mittlere” Geschwindigkeit? Die Teilchen bewegen sich alle in unterschiedliche Richtungen und nicht alle gleich schnell.
Ein paar Gramm einer Flüssigkeit entsprechen grob einem Mol von Teilchen, ob Atome oder Moleküle. Ein Mol ist definiert als \(6.022 \cdot 10^{23}\) Teilchen. Das sind sehr, sehr, sehr viele Teilchen mit unterschiedlichen Geschwindigkeiten!
Wir können die auftretenden Geschwindigkeiten in einer Wahrscheinlichkeitsverteilung auftragen, mit der horizontalen Achse für die Geschwindigkeit und mit der vertikalen Achse für die Auftretenswahrscheinlichkeit.
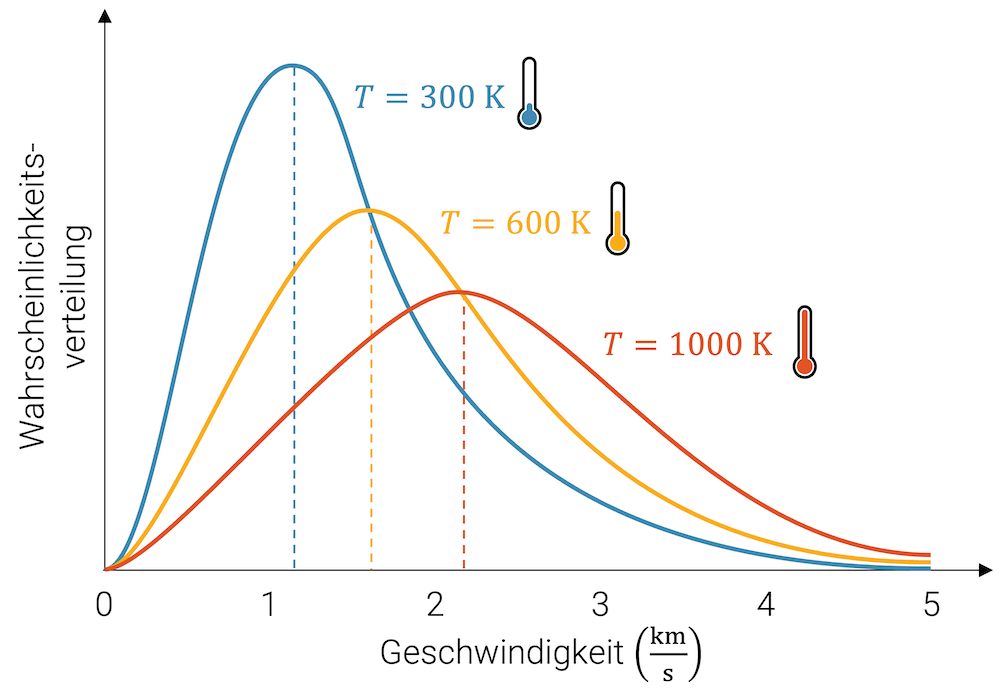
Bei einer sommerlichen Raumtemperatur (ca. 27 °C = 300 K) kriegen wir für ein Gas die Verteilung in blau. Die meisten Teilchen haben eine Geschwindigkeit von ca. 1 km/s – was übrigens eine extrem grosse Geschwindigkeit ist!
Es gibt aber auch kleinere Geschwindigkeiten, bis fast null, wenn auch deren Wahrscheinlichkeit sehr klein ist.
Höhere Geschwindigkeiten kommen ebenfalls vor, jedoch bis knapp unter \(1.1\cdot 10^3\;\frac{\text{m}}{\text{s}}\).
Wenn wir die Temperatur um 300 °C erhöhen, auf 327 °C = 600 K ist es immer noch so. Wir haben immer noch die kleinen Geschwindigkeiten und es gibt immer noch die grossen Geschwindigkeiten. Allerdings gibt es statistisch gesehen weniger von den kleinen und mehr von den grossen Geschwindigkeiten.
Die mittlere Geschwindigkeit ist grösser, bei höherer Temperatur.
Bei noch höherer Temperatur von von ca. 727 °C = 1000 K flacht die Verteilung noch mehr ab und verschiebt sich immer mehr nach rechts, hin zu grösseren Geschwindigkeiten.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.