Wärmeausdehnung

Längenausdehnung von Feststoffen

Aus der Diskussion der Temperatur wissen wir, dass die Teilchenbewegung Platz braucht. Je höher die Temperatur, desto stärker ist die Teilchenbewegung und desto mehr Platz werden die Teilchen beanspruchen, was zu einer Vergrösserung des Volumens führt. Diese Vergrösserung des Volumens ist prozentual sehr klein, d.h. von Auge in der Regel nicht sichtbar. Wenn wir aber einen sehr grossen Festkörper betrachten, dann kann die prozentuale Vergrösserung durchaus Millimeter oder Zentimeter ausmachen, die wir dann feststellen können.

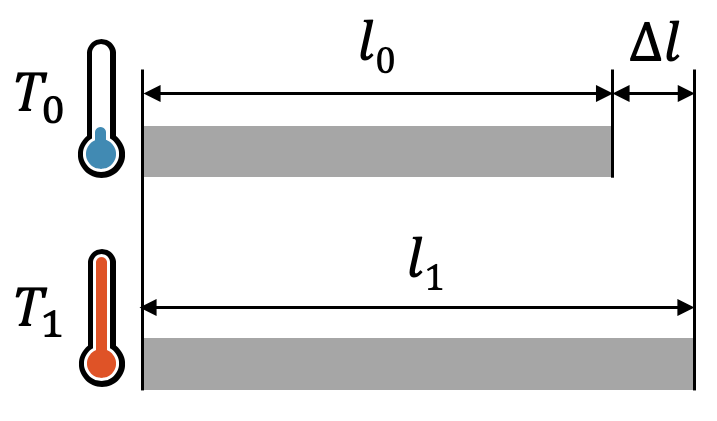
Die relative Längenausdehnung ist die absolute Verlängerung \(\Delta l\) pro ursprüngliche Länge \(l_0\):

\[ \frac{\Delta l}{l_0} \]

Wenn wir z.B. eine Metallstange von \(l_0=1\;\text{m}\) Länge anschauen, dann wird sie sich bei einer bestimmten Temperaturerhöhung verlängern um \(\Delta l\). Nehmen wir eine zweite solche Metallstange, dann wird diese sich natürlich auch um \(\Delta l\) verlängern, wenn wir sie auf die gleiche Temperatur bringen.

Kombinieren wir die beiden Stangen zu einer Stange von \(2l_0 = 2\;\text{m}\), dann summiert sich die absolute Längenänderung zu \(2 \Delta l\). Die relative Längenänderung ist aber immer noch die Gleiche, auch wenn die absolute Verlängerung jetzt natürlich doppelt so gross ist:

\[ \frac{\Delta l}{l_0} = \frac{2\Delta l}{2l_0} \]

Die relative Verlängerung ist abhängig von der Temperaturdifferenz \(\Delta T\) und vom Material. Unterschiedliche Materialien reagieren unterschiedlich auf eine Erhöhung der Temperatur. Um dies zu berücksichtigen, kann der sog. Längenausdehnungskoeffizient \(\alpha\) als Materialkonstante aus Tabellen gezogen werden. Die relative Längenänderung wird dann mit folgender Gleichung berechnet:

\[ \frac{\Delta l}{l_0} = \alpha \cdot \Delta T \] 

Beispiel

Eine Stahlbrücke ist am kältesten Tag 30 m lang. Um wie viel verlängert sie sich bei \(\Delta T = 60\;\text{K}\)?

(\(\alpha_{Stahl} = 11.7 \cdot 10^{−6}\;\text{K}^{−1}\))

---

Wir nehmen die Gleichung für die Berechnung der Längenausdehnung und lösen sie nach der absoluten Längenänderung \(\Delta l\) auf:

\[ \Delta l = l_0 \cdot \alpha \Delta T = 30\;\text{m} \cdot 11.7 \cdot 10^{−6}\;\text{K}^{−1} \cdot 60\;\text{K} = 0.021\;\text{m} = \underline{21\;\text{mm}} \]

Es braucht eine grosse Struktur von \(30\;\text{m}\) Länge, um eine absolute Längenänderung von gerade zwei Zentimetern zu erhalten. Allerdings führt eine Vernachlässigung dieser relativ kleinen Längenänderung zu sehr grossen Spannungen und schliesslich zu erheblichen Schäden.

Beispiel

Bimetalle sind Metallstreifen aus zwei unterschiedlichen Metallen. Das eine Metall dehnt sich stärker aus, als das andere Metall. Wenn ein Bimetallstreifen erwärmt (oder abgekühlt) wird, entsteht durch die unterschiedliche Ausdehnung der beiden Metalle ein Ungleichgewicht und der Streifen krümmt sich. Sobald er wieder zur ursprünglichen Temperatur zurückkehrt, wird er wieder gerade.

Wie muss ein Bimetallstreifen in einem Bügeleisen eingesetzt werden, damit er bei erreichter Heiztemperatur den Stromfluss unterbricht?

---

Wir brauchen einen Bimetallstreifen, der im “kalten” Zustand Kontakt gibt und so den Stromfluss ermöglicht. Bei höherer Temperatur soll er sich so biegen, dass er den Kontakt unterbricht.

Um dies zu erreichen, muss in der obigen Skizze das Bimetall so platziert werden, dass das stärker ausdehnende Metall (rot) mit dem grösseren Längenausdehnungskoeffizienten \(\alpha\) oben ist und unten das Metall mit dem kleineren Längenausdehnungskoeffizienten. Im geraden Zustand fliesst der Strom durch den Bimetallstreifen und über die berührte Spitze weiter zum Heizelement.

Sobald die Temperatur im Bügeleisen den gewünschten Wert erreicht hat, biegt sich das Bimetall genug stark, so dass der Kontakt unterbrochen wird und kein Strom mehr fliessen kann. Das Heizelement kriegt keinen elektrischen Strom mehr und wird erst wieder heizen, sobald die Temperatur wieder etwas heruntergekommen ist und der Bimetallstreifen dadurch wieder gerade geworden ist.

Ein temperaturabhängiger, automatischer Schalter wird auch Thermostat genannt. Wir haben im Haushalt sehr viele Thermostate im Einsatz. Ein bekanntes Beispiel ist der Thermostat im Wasserkocher, dessen “Klicken” gut hörbar ist.

Volumenausdehnung

Bei langen Strukturen wirkt sich die Ausdehnung durch die stärkere Teilchenbewegung in der Länge aus. Grundsätzlich dehnt sich eine Metallstange natürlich auch in ihrer Breite etwas aus. Das es aber die gleiche relative Längenausdehnung \(\frac{\Delta l}{l_0}\) ist, ist die absolute Längenänderung \(\Delta l\) unbedeutend klein. In anderen Worten: Eine Stahlbrücke hat in allen Richtungen die gleiche relative Ausdehnung. In ihrer Länge entstehen absolute Längenänderungen in der Grössenordnung von Zentimetern und diese müssen berücksichtigt werden. In ihrer Breite oder Höhe sind die Längenänderungen so klein, dass sie oft ignoriert werden können. Ausserdem ist die Brücke in der Breite und Höhe nicht gleich “eingespannt” wie in der Länge.

Was ich damit sagen will: Das grundsätzliche Phänomen der Wärmeausdehnung ist eigentlich immer eine Volumenausdehnung. Nur manifestiert sie sich öfters bei langen Strukturen mit der Längenausdehnung.

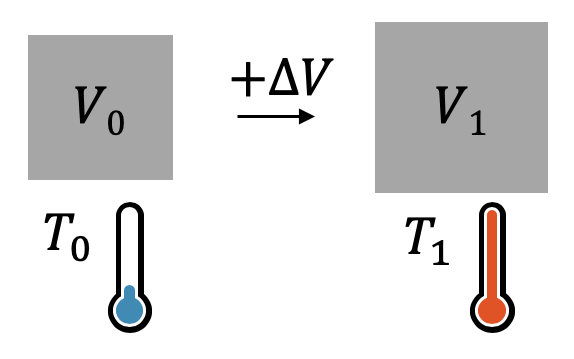
Bei der Besprechung der Funktionsweise eines Flüssigkeitsthermometers haben wir gesehen, dass die gefärbte Flüssigkeit sich mit höherer Temperatur ausdehnt. Im Flüssigkeitsthermometer hat sie nur die Möglichkeit über die dünne Glasröhre, womit die Flüssigkeitssäule entsteht, die uns die Temperatur auf einer Skala angibt.

Die relative Volumenänderung \(\frac{\Delta V}{V_0}\) ist wieder das Verhältnis der absoluten Volumenänderung \(\Delta V\) zum ursprünglichen Volumen \(V_0\). Gleich wie bei der Längenänderung, wird die Volumenänderung mit einer Gleichung berechnet, die die Temperaturdifferenz \(\Delta T\) und eine Materialgrösse beinhaltet, den Volumenausdehnungskoeffizienten \(\gamma\):

\[ \frac{\Delta V}{V_0} = \gamma \cdot \Delta T \]

Beispiel

Du erwärmst \(100\;\text{ml}\) Ethanol um \(30\;\text{°C}\). Wie gross ist das Volumen jetzt?

(\(\gamma_{Ethanol} = 1.40 \cdot 10^{−3}\;\text{K}^{−1}\))

---

Wir nehmen die Gleichung für die Berechnung der Volumenausdehnung und lösen sie nach der absoluten Volumenänderung \(\Delta V\) auf:

\[ \Delta V = V_0 \cdot \gamma \Delta T = 100\;\text{ml} \cdot 1.40 \cdot 10^{−3}\;\text{K}^{−1} \cdot 30\;\text{K} = 4.2\;\text{ml} \]

Beachte, dass wir für die Temperaturdifferenz die Temperatureinheiten Celsius und Kelvin einfach vertauschen können, denn sie sind nur absolut gesehen anders, für Differenzen \(\Delta T\) ist die Schrittlänge gleich gross.

Wir haben jetzt als Zwischenresultat die absolute Volumenänderung, d.h. wir wissen, um wie viel das Volumen durch die Erwärmung zunehmen wird. Wir addieren diese Zunahme zum ursprünglichen Volumen und erhalten so das neue Volumen:

\[ V_1 = V_0 + \Delta V = 100\;\text{ml} + 4.2\;\text{ml} = \underline{104.2\;\text{ml}} \]

Zusammenhang zwischen Volumen- und Längenausdehnung

Die neue Länge \(l_1\) durch eine Erwärmung erhalten wir, indem wir die absolute Längenänderung \(\Delta l\) zur ursprünglichen Länge \(l_0\) addieren. Wir setzen für \(\Delta l\) den Ausdruck aus der Längenausdehnung ein und klammern schliesslich \(l_0\) aus:

\[ l_1 = l_0 + \Delta l = l_0 + l_0 \alpha \Delta T = l_0 \cdot \big( 1 + \alpha \Delta T \big) \]

Die Volumenausdehnung kann nun aufgrund der Längenausdehnung berechnet werden. Das Volumen eines Quaders ist die dritte Potenz seiner Längen. Wir setzen jetzt die Längen \(l_1\) ein und multiplizieren aus:

\[ V_0 = l_0^3 \quad \rightarrow \quad V_1 = l_1^3 \]

\[ V_1 = l_1^3 = \big( l_0 \cdot ( 1 + \alpha \Delta T ) \big)^3 = l_0^3 \cdot \big( 1 + \alpha \Delta T \big)^3 \]

\[ = V_0 \cdot \Big( 1 + 3(\alpha \Delta T) + 3(\alpha \Delta T)^2 + (\alpha \Delta T)^3 \Big) \]

Wir dividieren \(V_1\) durch \(V_0\) und erhalten:

\[ \require{cancel} \frac{V_1}{V_0} = 1 + 3(\alpha \Delta T) + \cancel{3(\alpha \Delta T)^2} + \cancel{(\alpha \Delta T)^3} \]

Die zwei letzten Summanden fallen weg, weil der Längenausdehnungskoeffizient \(\alpha\) eine sehr kleine Zahl ist. Wenn wir diese sehr kleine Zahl quadrieren oder in die dritte Potenz bringen, wird die Zahl noch viel kleiner, d.h. \(\alpha^2 \rightarrow 0\) und \(\alpha^3 \rightarrow 0\) und der betroffene Summand wird vernachlässigbar klein. Somit bliebt uns ein vereinfachter Ausdruck:

\[ \frac{V_1}{V_0} \approx 1 + 3(\alpha \Delta T) \]

Jetzt multiplizieren wir wieder mit \(V_0\) und ersetzen \(V_1 = V_0 + \Delta V\):

\[ V_1 = V_0 + \Delta V \approx V_0 + 3V_0(\alpha \Delta T) \]

\[ \Delta V \approx 3V_0(\alpha \Delta T) \]

Schliesslich erhalten wir einen Ausdruck für die relative Volumenänderung, den wir mit dem Ausdruck mit dem Volumenausdehnungskoeffizienten \(\gamma\) vergleichen:

\[ \frac{\Delta V}{V_0} \approx 3(\alpha \Delta T) \approx \gamma \Delta T \]

Daraus folgt der Zusammenhang zwischen \(\gamma\) und \(\alpha\):

\[ \gamma \approx 3\alpha \]

Wenn wir also den Volumenausdehnungskoeffizienten \(\gamma\) nicht haben, können wir ihn aus dem Längenausdehnungskoeffizienten \(\alpha\) bestimmen bzw. umgekehrt. Wenn experimentell der eine Koeffizient einfacher zu bestimmen ist als der andere, kann so eine Messung beide Koeffizienten liefern.