Normalkraft

Die Normalkraft \(F_N\) ist eine Reaktionskraft eines Körpers, wenn er von einem anderen Körper berührt wird. Sie zeigt senkrecht (“normal”) zur Berührungsfläche und ist im Betrag genau gleich der Aktionskraft, d.h. der Kraft, mit welcher der andere Körper drückt.

Die Normalkraft ist die Reaktionskraft eines Festkörpers auf einen Druck durch einen anderen Festkörper. Mit “normal” ist die geometrische Verwendung des Worts für “senkrecht” gemeint. Die Normalkraft ist nämlich genau senkrecht zur Berührungsfläche zwischen den beiden Körpern.

Auf den ersten Blick erscheint es seltsam, dass eine lebloser Körper, wie der Boden oder die Tischplatte, in der Lage ist, eine Kraft auszuüben. Versteht man die Normalkraft als eine Reaktionskraft im Sinne von Newtons Drittem Gesetz, so gibt es nur dann eine Normalkraft, wenn sie durch eine andere Kraft (Aktionskraft) hervorgerufen wird. Die beiden Kräfte bilden ein Kräftepaar für die Wechselwirkung der gegenseitigen Berührung. Letztendlich handelt es sich einfach um die elektromagnetische Abstossungskraft (Coulombkraft) der Elektronen der beiden Körper.

Die üblichste aller Normalkräfte ist die Reaktionskraft des Bodens auf einen Körper, z.B. auf unsere Füsse. Diese Normalkraft zeigt senkrecht zur horizontalen Erdoberfläche und somit senkrecht nach oben. Sie kompensiert die Gewichtskraft, die genau umgekehrt gerichtet ist, nämlich senkrecht zur Erdmitte hin.

Wenn wir z.B. mit dem Finger gegen einen Knopf drücken, so reagiert dieser ebenfalls mit einer Normalkraft. Wenn der Finger von rechts nach links drückt, zeigt die Normalkraft als Reaktion genau in umgekehrter Richtung und senkrecht zur Berührungsfläche von links nach rechts.

Normalkraft als variierende Reaktionskraft

Die Richtung der Normalkraft ist immer senkrecht zur Ebene und damit klar gegeben. Der Betrag der Normalkraft hängt von der Situation ab und ist damit wesentlich interessanter.

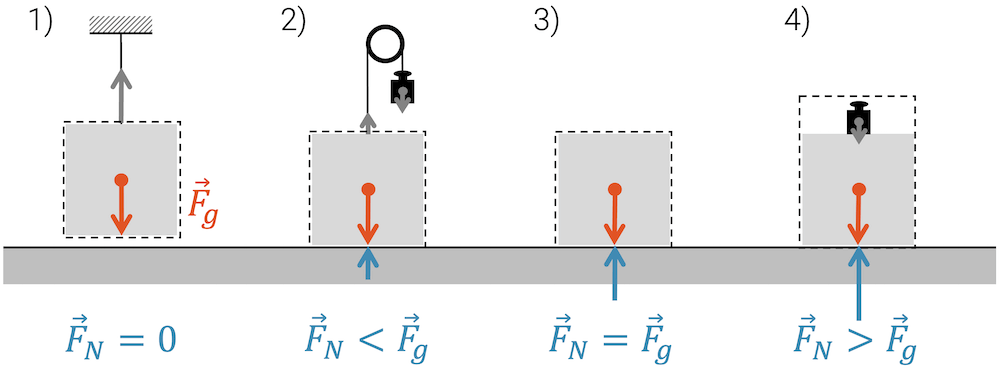
Betrachten wir die Wechselwirkung zwischen einem Klotz und einer Tischfläche: Die obigen vier Situationen zeigen verschieden grosse Normalkräfte.

Im ersten Fall (ganz links) hängt der Klotz an einem Faden, der an der Decke angemacht ist. Der Klotz schwebt unmittelbar über der Tischfläche und berührt diese gerade noch nicht. Weil wir keine Berührung haben, folgt daraus auch, dass wir keine Normalkraft haben. Der Betrag der Normalkraft ist deshalb null: \(F_N = 0\)

Im zweiten Fall von links, hängt der Klotz noch immer an einem Faden. Jedoch wird er weniger stark zurückgezogen, denn am anderen Ende des Fadens hängt nur ein kleines Gewicht. Der Faden kann deshalb den Klotz nicht mehr ganz anheben, aber er wirkt trotz allem mit einer gewissen Kraft. Der Klotz liegt auf dem Tisch auf und wir haben eine nicht verschwindende Normalkraft. Da der Klotz nicht mit vollem Gewicht auf den Tisch drückt, sondern mit einer um die Fadenkraft reduzierte Kraft, ist auch die Normalkraft kleiner als die Gewichtskraft des Klotzes: \(F_N < F_g\).

Der dritte Fall ist der klassische Fall für ein ruhendes Objekt auf einer waagrechten Oberfläche. Der Klotz drückt mit voller Gewichtskraft auf die Tischfläche und diese drückt mit der gleichen, aber entgegengesetzten Normalkraft (Newton 3) zurück. Die Normalkraft ist also vom Betrag her gleich gross wie die Gewichtskraft: \(F_N = F_g\).

Im vierten Fall, rechts, legen wir auf den Klotz eine zusätzliche Masse auf. Damit drückt der Klotz jetzt nicht nur mit seiner eigenen Gewichtskraft, sondern zusätzlich mit der Gewichtskraft der kleinen Masse. Damit ist die Normalkraft gleich der Summe beider Gewichtskräfte, aber sicherlich grösser als die Gewichtskraft des Klotzes: \(F_N > F_g\).

Zusammenfassend halten wir fest: Der Betrag der Normalkraft passt sich im Sinne einer Reaktionskraft auf den Betrag der Aktionskraft an. Drücken wir gar nicht, gibt es auch keine Normalkraft. Drücken wir leicht, ist die Normalkraft entsprechend klein. Drücken wir stark, reagiert die Normalkraft mit einem grösseren Betrag etc. Tatsächlich ist es so, dass die Normalkraft im Betrag immer genau gleich gross der senkrechten Komponente der Aktionskraft ist, jedoch mit umgekehrter Richtung.

Normalkraft an der schiefen Ebene

Wir wissen, dass die Normalkraft senkrecht zur Ebene zeigt und ihr Betrag sich als Reaktion zur drückenden Kraft einstellt. Wenn diese drückende Kraft senkrecht zur Fläche wirkt, dann ist die Normalkraft gemäss Newton 3 gleich im Betrag und umgekehrt in der Richtung. Was passiert jedoch, wenn die Kraft schräg zur Ebene wirkt?

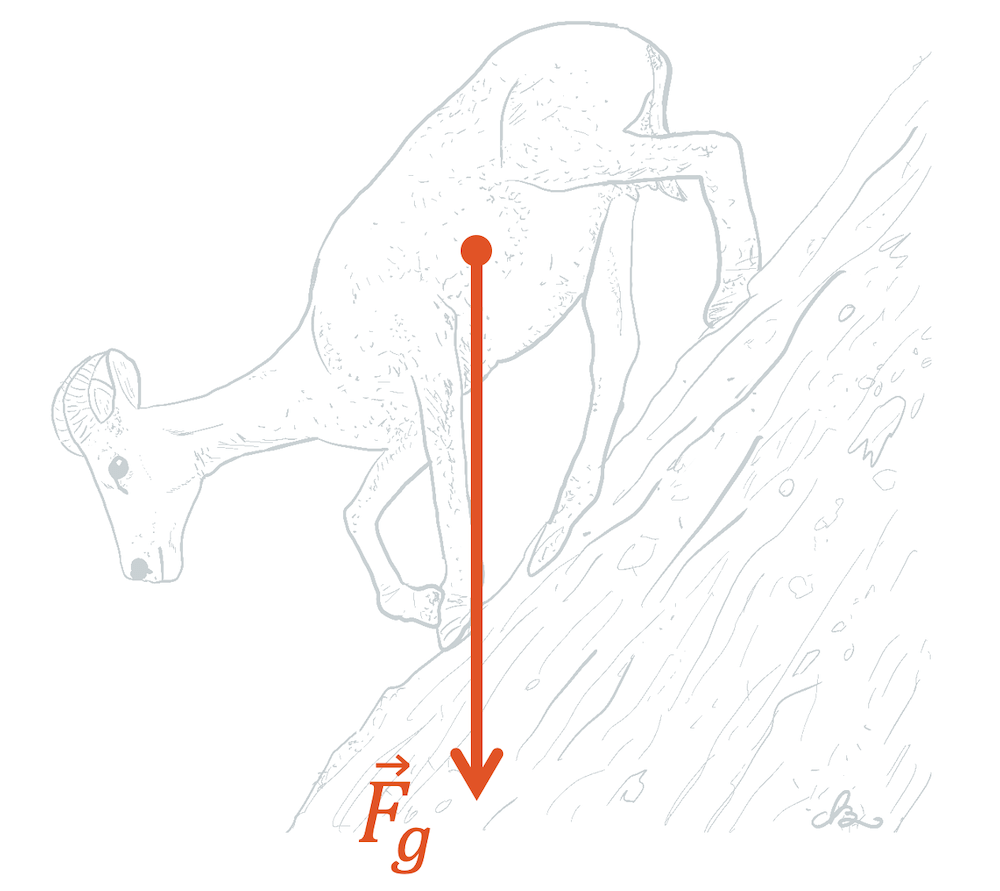
Wir betrachten den Fall der schiefen Ebene. Die Gewichtskraft \(F_g\) wirkt immer senkrecht zum Zentrum der Erde und damit bei einer schiefen Ebene halt immer schräg zur Ebene. Es lohnt sich jetzt die Gewichtskraft in zwei Teilkräfte aufzuteilen. Wir wählen die beiden Richtungen parallel zur Ebene (Abkürzung “\)\parallel\)”) und senkrecht zur Ebene (Abkürzung “\)\perp\)”):

\[ \vec{F}_g = \vec{F}_{g \parallel} + \vec{F}_{g \perp} \]

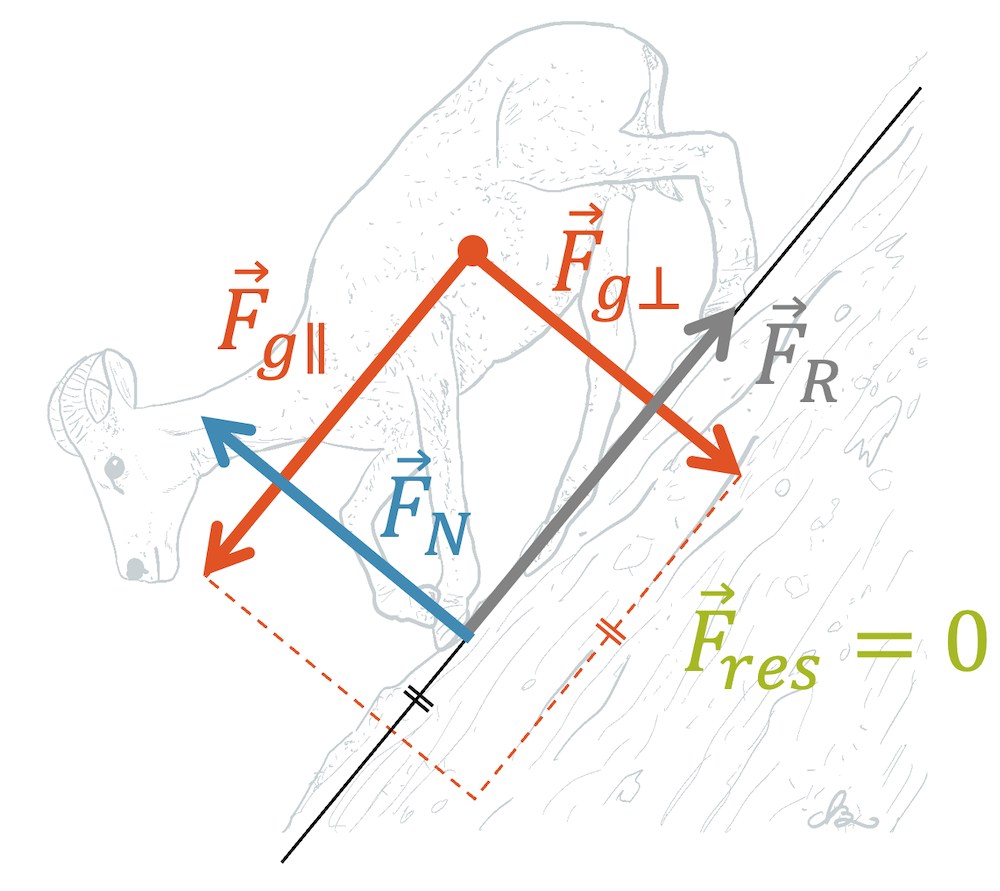
Als Erstes betrachten wir nur die Richtung senkrecht zur Ebene. Das Tier drück mit der Senkrechtkomponente der Gewichtskraft \(\vec{F}_{g \perp}\) gegen den Fels. Dieser reagiert jetzt mit einer Normalkraft, die genau gleich gross ist im Betrag, aber umgekehrt in der Richtung. Die beiden Kräfte heben sich auf und wir haben gemäss Newton 1 keine Beschleunigung in der betrachteten Richtung.

Als Zweites betrachten wir die Richtung parallel zur Ebene. Wir haben die Parallelkomponente der Gewichtskraft \(\vec{F}_{g \parallel}\) schräg nach unten. Wenn der Fels allglatt wäre, hätten wir keinerlei Reibung und das Tier würde aufgrund dieser Teilkraft den Hang hinunterrutschen (Beschleunigung aufgrund von Newton 2). Das Tier hat aber genug Halt, um in dieser Position zu verharren. Die Kraft, die dazu nötig ist, ist die Haftreibungskraft \(\vec{F}_R\), die analog zur Normalkraft sich als Reaktion einstellt, so dass die Kraft \(\vec{F}_{g \parallel}\) aufgehoben wird. Wir haben demnach auch in paralleler Richtung zur Oberfläche keine Beschleunigung.

In Summe reagiert der Fels gegenüber dem Tier mit einer Normalkraft und einer Haftreibungskraft, so dass wir Kräftegleichgewicht haben: \(\vec{F}_{res}=0\).