Image by Jumilla
Kräfte sind Vektorgrössen und können deshalb als solche addiert werden. Die Summe von Kraftvektoren wirkt in gleicher Art wie die einzelnen Kräfte zusammen. Der umgekehrte Prozess ist ebenfalls äquivalent: Eine einzelne Kraft kann in mehrere Teilkräfte zerlegt werden, die in Summe die ursprüngliche Kraft ergeben.
Die resultierende Kraft ist die Summe aller Kräfte, die auf ein System (z.B. einen Gegenstand) wirken. Die resultierende Kraft steht stellvertretend für alle wirkenden Kräfte und vereinfacht somit die Analyse des Systems, z.B. hinsichtlich des Kräftegleichgewichts oder für die Anwendung der Newton’schen Gesetze.
Für die schiefe Ebene empfiehlt sich eine Zerlegung der Kraft (z.B. Gewichtskraft) in zwei Teilkräfte, eine zur schiefen Ebene parallele Komponente \(\vec{F_{\parallel}}\) und eine senkrechte Komponente \(\vec{F_{\perp}}\).
Kräfte addieren
Kräfte sind Vektorgrössen und werden als solche addiert. Vektoren addiert man, indem sie miteinander verkettet werden. Die Reihenfolge ist egal, genauso wie es nicht darauf ankommt, in welcher Reihenfolge wir Zahlen addieren. Dann verbindet man den Anfangspunkt und den Endpunkt der Kette. Diese Verbindung bildet den Summenvektor bzw. die Summenkraft.
In den folgenden drei Beispielen werden zwei Kräfte, \(\vec{F_1}\) und \(\vec{F_2}\) miteinander addiert und es entsteht die Summe \(\vec{F_3}\):
\[ \vec{F_1}+\vec{F_2} = \vec{F_3} \]
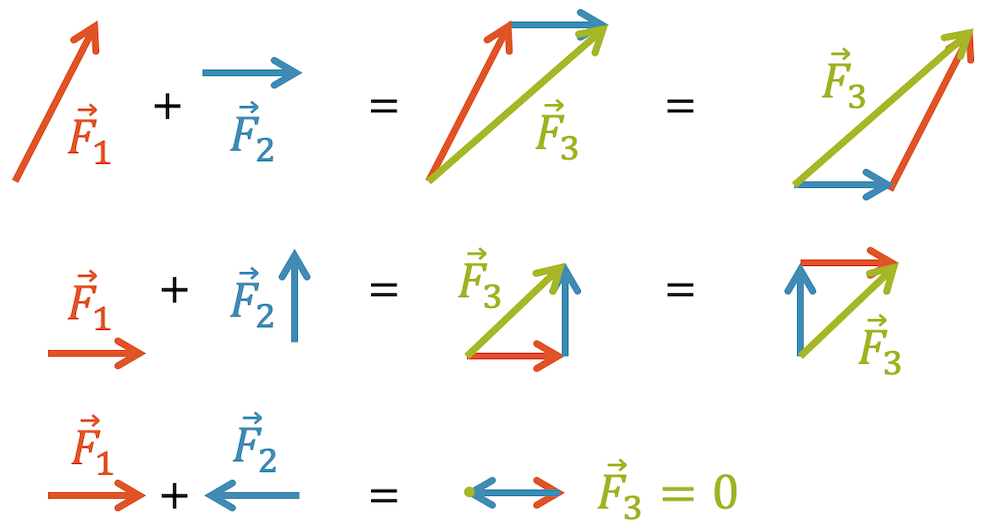
Beachte im letzten Beispiel, dass zwei Kräfte mit gleichem Betrag (gleiche Pfeillänge), jedoch mit entgegengesetzter Richtung, sich genau aufheben. Die Summe ist null.
Da die Kraft \(\vec{F_3}\) in gleicher Art wirkt, wie die Summe \((\vec{F_1} + \vec{F_2})\), besteht physikalisch kein Unterschied. Wir nennen das auch physikalisch äquivalent, d.h. der betrachtete Gegenstand oder Körper wird sich in beiden Fällen genau gleich verhalten, egal ob \(\vec{F_1}\) und \(\vec{F_2}\) wirken oder nur \(\vec{F_3}\).
Beispiel
An einem Drachen wirken zwei Kräfte: Die Gewichtskraft \(\vec{F_1}\) und die Windkraft \(\vec{F_2}\). Addieren Sie die beiden Kräfte grafisch.
Wir zeichnen das Parallelogramm, das durch die beiden Kräfte aufgezogen wird. Dann verbinden wir den Angriffspunkt der Kräfte mit dem neuen Eckpunkt des Parallelogramms, so dass wir die Diagonale kriegen. Diese Diagonale entspricht der Summe \((\vec{F_1}+\vec{F_2})\) bzw. \((\vec{F_2}+\vec{F_1})\).
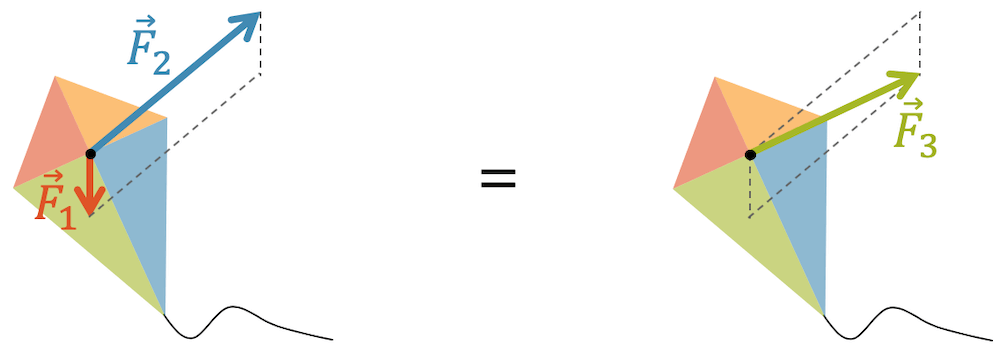
Resultierende Kraft
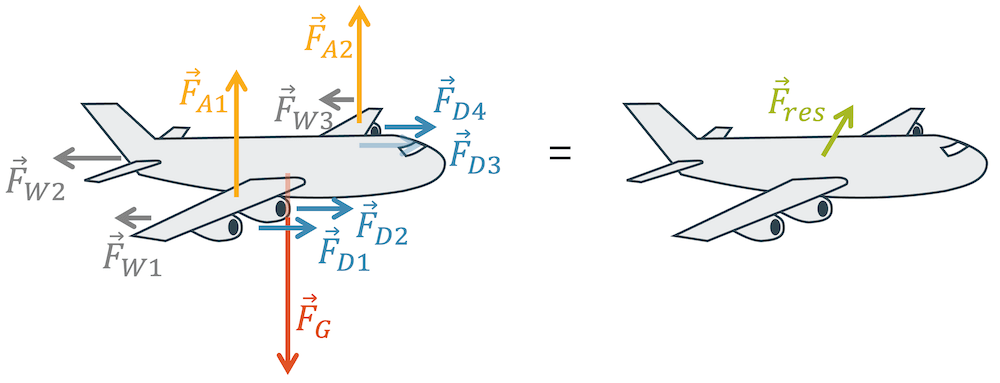
Wenn wir zwei Kräfte addieren können, so können wir auch eine dritte Kraft dazu addieren usw. Schliesslich haben wir alle Kräfte zu einer einzigen Summenkraft addiert. Die Summe aller Kräfte, die auf ein System wirken, ist die resultierende Kraft \(\vec{F}_{res}\).
Der Vorteil der resultierenden Kraft ist, dass wir von nur einer Kraft sprechen, was die Sache wesentlich vereinfacht und übersichtlich macht. Das Starke ist aber, dass wir trotzdem das vollständige Problem betrachten! Die Summe aller Kräfte wirkt gleich, wie alle einzelnen Kräfte zusammen.
Bevor wir eine Aussage zu einem System machen können, addieren wir alle Kräfte und vereinfachen somit die Problemstellung. Aufgrund der resultierenden Kraft machen wir dann unsere Aussage. Wenn beispielsweise die resultierende Kraft verschwindet (\(\vec{F}_{res} = 0\)), d.h. wenn alle Kräfte sich gegenseitig aufheben, dann haben wir Kräftegleichgewicht. Wir können Newtons Erstes Gesetz anwenden und folgern, dass das Flugzeug mit konstanter Geschwindigkeit fliegt, sowohl im Betrag, wie auch in der Richtung.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Kommentar oder Frage schreiben
Du musst angemeldet sein, um einen Kommentar abzugeben.