Fluchtgeschwindigkeit

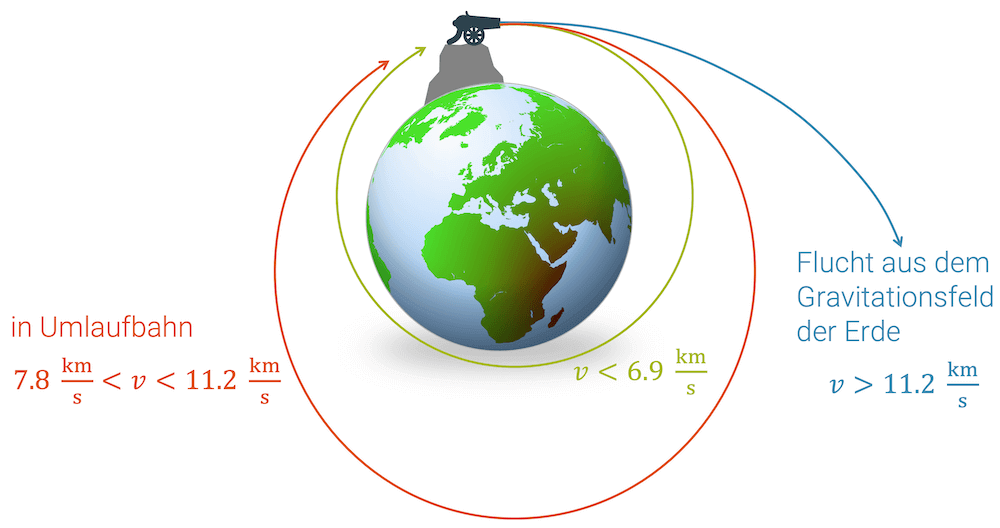
Wie wir bei der Besprechung Newtons’ Gedankenexperiment gesehen haben, ist die Geschwindigkeit der Kanonenkugel entscheidend. Um in Umlaufbahn zu kommen (und zu bleiben), braucht es eine hohe Bahngeschwindigkeit von mindestens etwa 7.8 km/s. Ist die Kanonenkugel zu langsam, fällt sie früher oder später auf die Erde herunter. Soll das Gravitationsfeld der Erde ganz verlassen werden, ist eine noch grössere Geschwindigkeit von etwa 11.2 km/s nötig, der sog. Fluchtgeschwindigkeit.

Das “Flüchten” aus dem Potenzialtopf kann mit einer Energiebetrachtung am besten verstanden werden. Wir sind auf der Erde und damit in einer bestimmten Tiefe des Potenzialtopfs. Unsere potenzielle Energie ist um einen bestimmten Betrag unter null. Unser Ziel, die Weiten des Weltalls, ist auf dem Niveau null. Wir müssen die ganze Tiefe des Topfs überwinden und das mit Geschwindigkeit, d.h. mit genügend kinetischer Energie.

Wir bestimmen zuerst die Tiefe des Potenzialtopfs und starten mit dem Ausdruck für die Hubarbeit im Gravitationsfeld, die nötig ist, um vom Abstand \(r_1\) zum Abstand \(r_2\) zu gelangen:

\[ W = \int_{r_1}^{r_2} F_G(r) dr = -G\,m_E\,m\cdot\big(\frac{1}{r_2}-\frac{1}{r_1}\big) \]

Der Abstand \(r_1\) ist ja der Erdradius \(r_1=r_E = 6’371\;\text{km}\). Der Abstand \(r_2\) ist theoretisch unendlich, denn wir möchten aus den Fängen der Erde kommen. Theoretisch wirkt die Gravitationskraft bis ins Unendliche. Physikalisch gesehen, reicht es aber, genug weit entfernt zu sein und da sprechen wir von einer Distanz, die sicherlich grösser ist als die Entfernung zum Mond, aber wir müssen z.B. beim Mars nicht Angst haben, wieder auf die Erde zurück zu fallen. Wir setzen einfach \(r_2 \rightarrow \infty\):

\[ W = \int_{r_E}^{\infty} F_G(r) dr = -G\,m_E\,m\cdot\big(\cancel{\frac{1}{\infty}}-\frac{1}{r_E}\big) = \frac{G\,m_E\,m}{r_E} \]

Wir haben jetzt die Hubarbeit, die es braucht, um \(1\,\text{kg}\) aus dem Potenzialtopf der Erde herauszuheben. Wir haben keinen Kran, der diese Aufgabe übernehmen kann, sondern einen Raketenantrieb, der uns genug “Schuss” gibt, um aus dem Topf zu kommen. Wir heben uns aus dem Topf und bezahlen die Hubarbeit mit kinetischer Energie. Wir setzen deshalb die kinetische Energie aufgrund der Geschwindigkeit \(v\) mit der benötigten Hubarbeit gleich. Die Masse \(m\) kürzt sich heraus:

\[ E_{kin} = \frac{1}{2}\cancel{m}v^2 = \frac{G\,m_E\,\cancel{m}}{r_E} = W \]

Jetzt lösen wir nach der Geschwindigkeit \(v\) auf, die dazu nötig ist und setzen die Gravitationskonstante \(G\), die Erdmasse \(m_E\) und den Erdradius \(r_E\) ein:

\[ v = \sqrt{\frac{2\,G\,m_E}{r_E}} = \sqrt{\frac{2 \; \cdot \; 6.674\cdot10^{-11}\,\frac{\text{m}^3}{\text{kg}\,\text{s}^2} \; \cdot \; 5.972 \cdot 10^{24} \, \text{kg}}{6.371 \cdot 10^{6}\,\text{m}}} = 11.2\,\frac{\text{km}}{\text{s}} \]

Wir erhalten so die minimale Geschwindigkeit, die uns erlaubt aus dem Potenzialtopf der Erde zu gelangen. Mit dieser Anfangsgeschwindigkeit würden wir am “Rand” des Topfs unsere kinetische Energie genau aufgebraucht haben und keine Geschwindigkeit mehr haben. Dieser Rand ist nie erreicht, da er eigentlich im Unendlichen liegt. Wir erkennen aber, dass das wirklich das theoretische Minimum ist, um überhaupt aus den Fängen der Erde loszukommen.