Freier Fall

Unabhängigkeit von der Masse

Schon im 17. Jahrhundert stellte Galileo Galilei (1564 – 1642) aus Pisa (Italien), einer der wichtigsten Begründer der neuzeitlichen Naturwissenschaft, die These auf, wonach der freie Fall für alle Körper gleich sein soll, unabhängig von ihrer Masse, ihrer Grösse oder Form.

Wir wissen aber aus Erfahrung, dass ein Stein viel schneller fällt als eine Vogelfeder. Experiment im Vakuum konnten jedoch zeigen, dass die Unterschiede der Fallgeschwindigkeiten einzig auf den Luftwiderstand zurückzuführen sind. Nimmt man den Luftwiderstand weg, fallen Stein und Feder genau gleich schnell zu Boden. Galileo Galilei konnte dieses Experiment selber nicht durchführen. Anlässlich einer Mondmission wurde dieses berühmte Experiment aber sogar auf dem Mond gefilmt. Ein Hammer und eine Feder fielen dabei tatsächlich genau gleich schnell.

Bewegungsgleichung für den freien Fall

Die allgemeinste Bewegungsgleichung mit einer gleichmässigen (d.h. konstanten) Beschleunigung \(a\) lautet:

\[ s_1 = s_0 + v_0 \Delta t + \frac{1}{2} a \Delta t^2 \qquad \text{(1)} \]

Auf den freien Fall bezogen, können wir \(s\) als die Fallstrecke definieren. Im Gegensatz zum \(s\) als Höhe, wie wir das bei der Diskussion des senkrechten Wurfs benutzt haben, nimmt jetzt das \(s\) für einen frei fallenden Gegenstand immer mehr zu. Die Geschwindigkeit des frei fallenden Gegenstands ist auch nach unten gerichtet und somit positiv. Sie nimmt auch immer mehr zu. Der Gegenstand fällt immer schneller, je länger er fällt. Schliesslich ist die Beschleunigung konstant positiv, da die Geschwindigkeit ja zunimmt. Die Bewegungsdiagramme ergeben deshalb folgendes Bild:

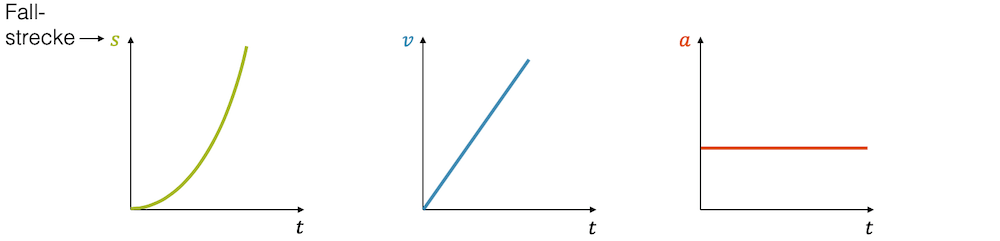
Der Betrag der Beschleunigung ist konstant positiv und beträgt: 

\[ a = g =9.81\frac{\text{m}}{\text{s}^2} \]

Mit \(g\) bezeichnen wir in der Physik die Erdbeschleunigung, die näherungsweise konstant ist.

In den meisten Fällen betrachten wir einen Gegenstand, der aus der Ruhe heraus (\(v_0 = 0\)) fallen gelassen wird. Die Fallstrecke \(s\) ist üblicherweise so definiert, dass der oberste Punkt, ab welchem der Gegenstand fallen gelassen wird, mit \(s=0\) definiert wird. Da der Gegenstand von dieser Position aus, seine Bewegung startet, gilt \(s_0=0\). Wir setzen alles in die Bewegungsgleichung (1) ein und erhalten die Bewegungsgleichung für den freien Fall:

\[ s = \frac{1}{2}gt^2 \]

Einsteins Äquivalenzprinzip

Wir wissen, dass auf der Erde, z.B. in einem Haus, die Erdbeschleunigung \(g\) herrscht. Alles wird zum Erdmittelpunkt hin beschleunigt, so auch der Ball, den wir loslassen.

Die gleiche Erdbeschleunigung wirkt auf eine Rakete. Wenn diese Rakete selber eine Beschleunigung von \(g\) erzeugt, würden sich beide Beschleunigungen aufheben und die Rakete würde wie ein Helikopter über der Erdoberfläche schweben \((v=0)\). Vielleicht hast du einmal ein Video gesehen von einer Space-X-Rakete, die so landet.

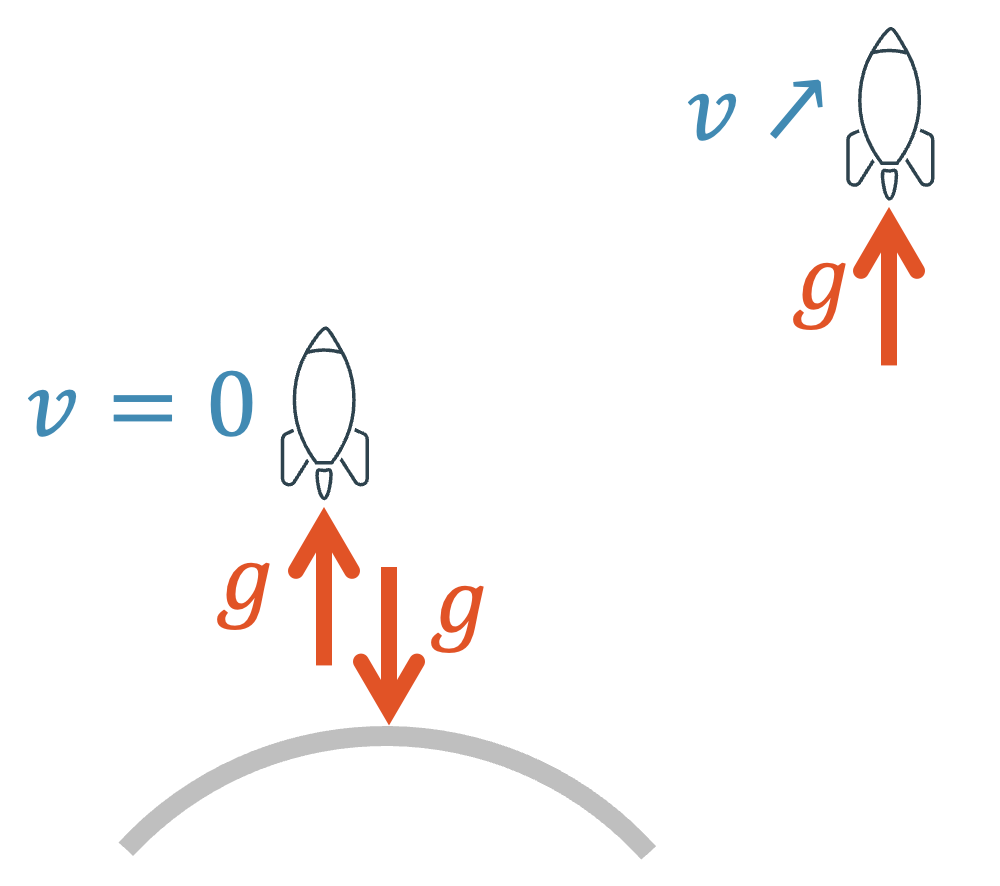
Bewegt sich die Rakete weg von der Erde, d.h. wenn sie genug weit weg vom Gravitationsfeld der Erde ist, wird sie bei gleicher Schubkraft tatsächlich schneller \((v \nearrow)\).

Für die Insassen der Rakete ändert sich aber gar nichts. Ob auf der Erde oder irgendwo im Weltall, ob die Rakete gegenüber der Erde still steht oder im Weltall immer schneller wird – alles fühlt sich an, wie im Haus. Ohne Fenster (und gleich eingerichtet), gäbe es keine Möglichkeit festzustellen, ob man sich im Haus oder in der beschleunigenden Rakete befindet! 🚀

Albert Einstein (1879 – 1955) ging mit dieser Überlegung noch einen Schritt weiter. Er hat sich überlegt, dass in den ersten beiden Bildern die Erde das Referenzsystem ist. Wir haben den Ball, das Haus und die Rakete im Bezug auf die Erde betrachtet.

Warum sollte die Erde dieses Privileg haben? Nur weil sie viel grösser ist als der Ball, das Haus oder die Rakete? Auch die Erde ist nur ein Objekt in einem viel grösseren Universum.

Er folgerte: Es gibt kein Referenzsystem, das mehr Berechtigung hat, als ein anderes!

Daraus folgt, dass die Erde und die beschleunigende Rakete, beide ein gültiges Referenzsystem sein können. Beide können die Beschleunigung \(g\) erzeugen, d.h. der Effekt der Masse der Erde ist äquivalent mit einer Rakete, die eine Beschleunigung von \(g\) erzeugen kann.

Die Erde erreicht dies, indem ihre grosse Masse die Raumzeit krümmt, so dass \(g\) entsteht. Die Rakete beschleunigt (im Sinne von Newton) und erzeugt damit den gleichen Effekt, d.h. es gibt für den Pfad in der Raumzeit keinen Unterschied zwischen der Erde und dieser Rakete! 😮