Beschleunigungs-Zeit-Diagramm
(a,t-Diagramm)

Üblicherweise wird die Zeit auf der horizontalen Achse und die momentane Beschleunigung \(a\) auf der vertikalen Achse aufgetragen.

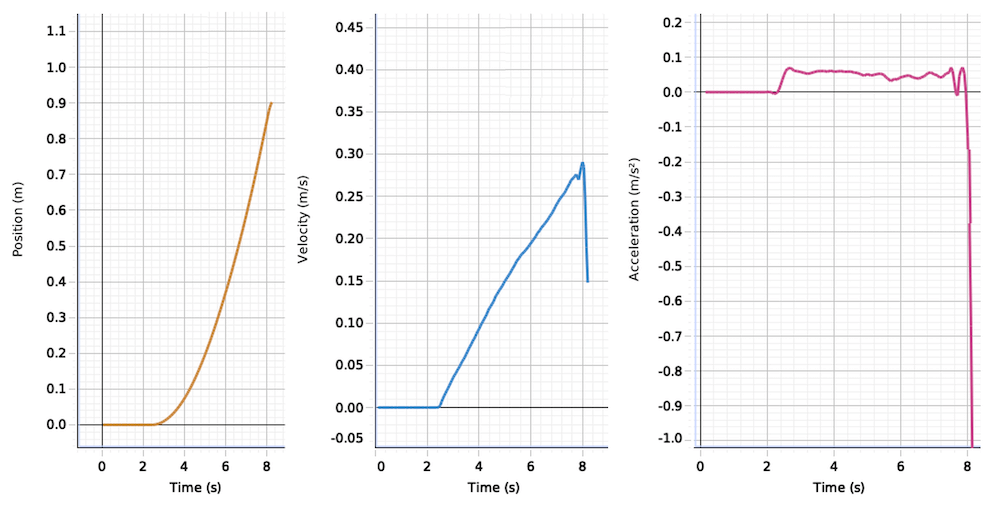
Erstellen eines a,t-Diagramms

Die Konstruktion eines a,t-Diagramms aufgrund eines v,t-Diagramms ist analog zur Beschreibung der Konstruktion eines v,t-Diagramms aufgrund eines s,t-Diagramms. Auch hier empfiehlt es sich, das a,t-Diagramm unterhalb des gegebenen v,t-Diagramms zu setzen und die zeitlichen Abschnitte zu übertragen.

Vorgehen:

• Geeigneten zeitlichen Abschnitt im v,t-Diagramm wählen
• Beschleunigung bestimmen (Steigungsdreieck: Steigung ergibt Beschleunigung)
• Beschleunigung im zeitlichen Abschnitt des a,t-Diagramms auf der richtigen Höhe übertragen
• Wiederholen für die nächsten Abschnitte

Im obigen Beispiel wird aus einem s,t-Diagramm zuerst ein v,t-Diagramm erstellt, danach entsteht ein a,t-Diagramm. Aus layout-technischen Überlegungen sind die drei Diagramme hier nicht übereinander, sondern nebeneinander dargestellt. Die relevanten Zeitabschnitte sind aber klar ersichtlich mit A, B und C gekennzeichnet.

Im Zeitabschnitt A ist die anfängliche Steigung noch null. Sie nimmt aber immer mehr zu und bleibt während der Zeitperiode B konstant. Im Zeitabschnitt C nimmt die Steigung kontinuierlich ab, bis sie schliesslich auch wieder null erreicht. Die Bewegung ist eine Vorwärtsbewegung mit einer aus dem Stand ansteigenden Geschwindigkeit, die eine Zeit lang (B) gehalten wird und dann wieder auf null abgebremst wird.

Das v,t-Diagramm erstellen wir zuerst für die Zeitperiode B. Wir ermitteln die Steigung des Verlaufs im s,t-Diagramm und tragen diesen Wert über die ganze Zeitperiode B als konstante Geschwindigkeit ein. Die Zeitperiode A konstruieren wir folgendermassen: Die Geschwindigkeit ist am Ende des Zeitabschnitts A gleich der vorhin ermittelten Geschwindigkeit aus B. Am Anfang der Zeitperiode A ist die Geschwindigkeit aber noch null. Wir nehmen jetzt einfach an, dass die Geschwindigkeit von null bis zum Niveau von B kontinuierlich zunimmt und verbinden deshalb die beiden Punkte. Das Gleiche machen wir jetzt auch im Zeitabschnitt C.

Anhand der Steigungen im v,t-Diagramm konstruieren wir jetzt das a,t-Diagramm. Der erste Abschnitt A hat eine konstante, positive Steigung. Wir ermitteln den Wert mit Hilfe eines Steigungsdreiecks und übertragen ihn auf der a-Achse im a,t-Diagramm. Die Beschleunigung \(a\) muss positiv sein, denn wir beschleunigen, um auf eine bestimmte Geschwindigkeit zu kommen.

Im Zeitabschnitt B ist die Geschwindigkeit konstant, d.h. sie ändert sich nicht und die Steigung ist null. Wir ziehen deshalb einen horizontalen Strich für \(a=0\) über den ganzen Zeitraum B.

Schliesslich betrachten wir den Zeitabschnitt C, wo die Geschwindigkeit abnimmt. Die Steigung ist negativ, aber konstant. Wir ermitteln den Wert der Steigung mit einem Steigungsdreieck und tragen diesen Wert im a,t-Diagramm ein, als horizontale Linie. Die Beschleunigung \(a\) ist negativ, da wir ja im Zeitabschnitt C abbremsen.

Darstellung einer Geschwindigkeit im a,t-Diagramm

Wir haben gesehen, dass die Fläche zwischen dem Verlauf und der t-Achse im v,t-Diagramm einer Strecke entspricht. Am besten erkennt man dies an den Einheiten:

\[ \Delta v \cdot \Delta t = \frac{\text{m}}{\text{s}} \cdot \text{s} = \text{m} \]

In analoger Weise ist eine Fläche im a,t-Diagramm eine Geschwindigkeit und zwar die mittlere Geschwindigkeit für den betrachteten Zeitraum:

\[ \Delta a \cdot \Delta t = \frac{\text{m}}{\text{s}^2} \cdot \text{s} = \frac{\text{m}}{\text{s}} \]