Inhalt
Das Wichtigste in Kürze
Der Schweredruck (hydrostatischer Druck) \(p\) ist der Druck, der durch das Eigengewicht eines Fluids (Flüssigkeit oder Gas) entsteht.
Beim Tauchen gilt die Faustregel: Der Druck im Wasser nimmt alle 10 Meter um 1 bar zu.
Nebst der Dichte und der Erdbeschleunigung ist der Schweredruck nur abhängig von der Höhe \(h\) der Wassersäule über dem Messpunkt. Der Schweredruck ist unabhängig von der Querschnittsfläche \(A\) (Pascal’scher Fassversuch)
\[ p \;\;=\;\; \rho g h \;+\; p_U \]
Ein allfälliger Umgebungsdruck \(p_U\) wirkt auf die Flüssigkeitsoberfläche und wird deshalb hinzuaddiert.
Videos
Druck aufgrund des Eigengewichts
Wir kennen das schon vom Schwimmbad: Je tiefer, desto stärker drückt der Wasserdruck auf unsere Ohren. Tatsächlich nimmt der Druck mit der Tiefe zu.
Mit Hilfe des Druckausgleichs, können wir erreichen, dass der äussere Druck etwa gleich gross ist, wie der innere Druck und es tut nicht mehr so weh.
Taucherinnen und Taucher lernen:
Pro 10 Meter Tiefe nimmt der Wasserdruck um 1 bar zu

Wir können den Grund dafür mit Hilfe der folgenden Analogie verstehen:
Ein kleiner Käfer ist unter einem Buch eingeklemmt. Das ist für seinen Panzer noch nicht so schlimm: Er spürt wenig Druck.
Wenn er aber unter einen ganzen Stapel von Büchern ist, spürt er viel Druck. Ein anderer Käfer, der im gleichen Stapel weiter oben eingeklemmt ist, wird nur wenig Druck spüren, weil er ja nur die Gewichtskraft der Bücher über ihm ertragen muss. Es ist egal, wie viele Bücher es unterhalb hat.

*hier wirkt nur noch der Luftdruck, aber kein Schweredruck vom Wasser mehr, © by Yangchen Brunner
Je grösser der “Stapel” des Fluids oberhalb ist, desto grösser ist der sog. Schweredruck (hydrostatischer Druck), d.h. ganz unten haben wie viel Druck, weiter oben wenig Druck und ganz oben eigentlich gar keinen Druck mehr.
Im Wasser, in allen Flüssigkeiten und sogar in Gasen gilt: Die Fluid-Teilchen stapeln sich und wir haben, wie beim Bücherstapel, unten eine grosse Gewichtskraft und damit viel Druck. Je weiter oben wir sind, desto kleiner wird der Schweredruck. Unmittelbar an der Oberfläche gibt es keinen hydrostatischen Druck mehr, wohl aber den allgemeinen Luftdruck.
Entscheidend ist die Höhe der Fluidsäule über dem Messpunkt.
“Der Luftdruck ist der Schweredruck der riesigen Luftsäule an Atmosphäre, die wir über unseren Köpfen haben!”
Berechnung des Schweredrucks
Für die Berechnung des Schweredrucks (hydrostatischer Druck) benutzen wir die folgende Formel:
\[ p \;\;=\;\; \rho \cdot g \cdot h \;+\; p_U \]
Der Schweredruck \(p\) ist natürlich abhängig von der Höhe \(h\) der Flüssigkeitssäule über dem Messpunkt. Was darunter liegt, spielt keine Rolle.
Je schwerer die Flüssigkeit, d.h. je grösser die Dichte der Flüssigkeit \(\rho\), desto schneller steigt der Schweredruck an.
Oft vergessen, aber genauso wichtig: Die Erdbeschleunigung \(g\) ist mitverantwortlich für den Schweredruck. Das ist nicht weiter verwunderlich, denn ohne Erdbeschleunigung hätten wir keine Gewichtskraft und damit auch keinen Schweredruck. Das Fluid wäre ja schwerelos, würde sich also nicht “stapeln”, sondern wie eine Kugel schweben. Es gäbe auch kein “oberhalb” und “unterhalb” mehr.
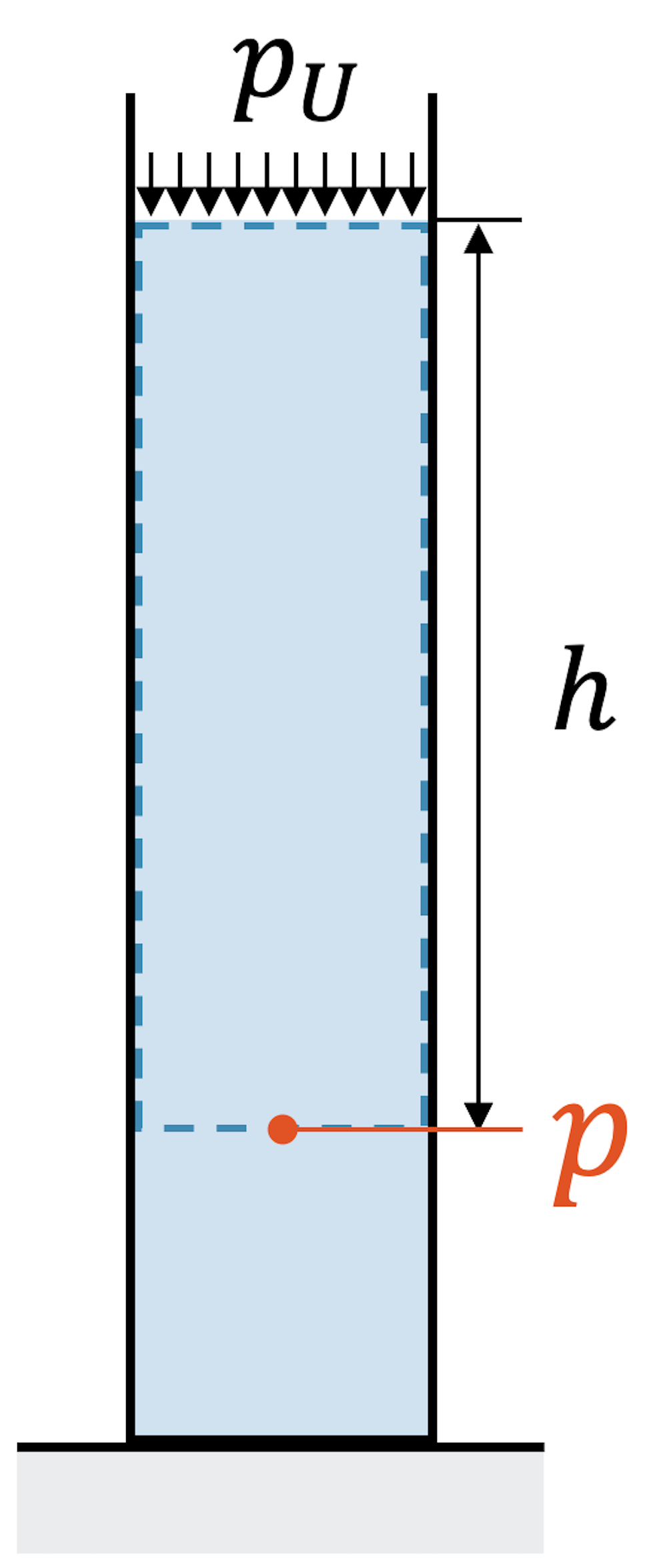
Der Druck \(p_U\) ist der Umgebungsdruck, d.h. der umgebende Luftdruck. Er ist stellvertretend für den Schweredruck der riesigen Luftsäule der Atmosphäre über unseren Köpfen! Wenn wir den Schweredruck berechnen, sollten wir deshalb nicht vergessen, dass auf den Stapel Wasser auch der Stapel Luft drückt.
Interessant ist, dass der Schweredruck komplett unabhängig ist von der Querschnittsfläche \(A\) oder deren Geometrie.
Es kommt nicht darauf an, ob es schlankes, breites, quaderförmiges oder zylindrisches Gefäss ist. Nur die Höhe der Flüssigkeitssäule über dem Punkt ist für den Schweredruck der entsprechenden Flüssigkeit relevant. Der französische Physiker und Mathematiker Blaise Pascal zeigte diese überraschende Eigenschaft mit Hilfe seines sog. Fassversuchs (siehe weiter unten).
Beispiel
Herleitung
Für die Herleitung des Schweredrucks betrachten wir eine Wassersäule in einem schlanken Behälter, z.B. in einem Messzylinder. Wir interessieren uns für den Druck auf einer beliebigen Höhe im Behälter. Wir werden diese Höhe \(h\) aber nicht von unten her messen, sondern von oben.
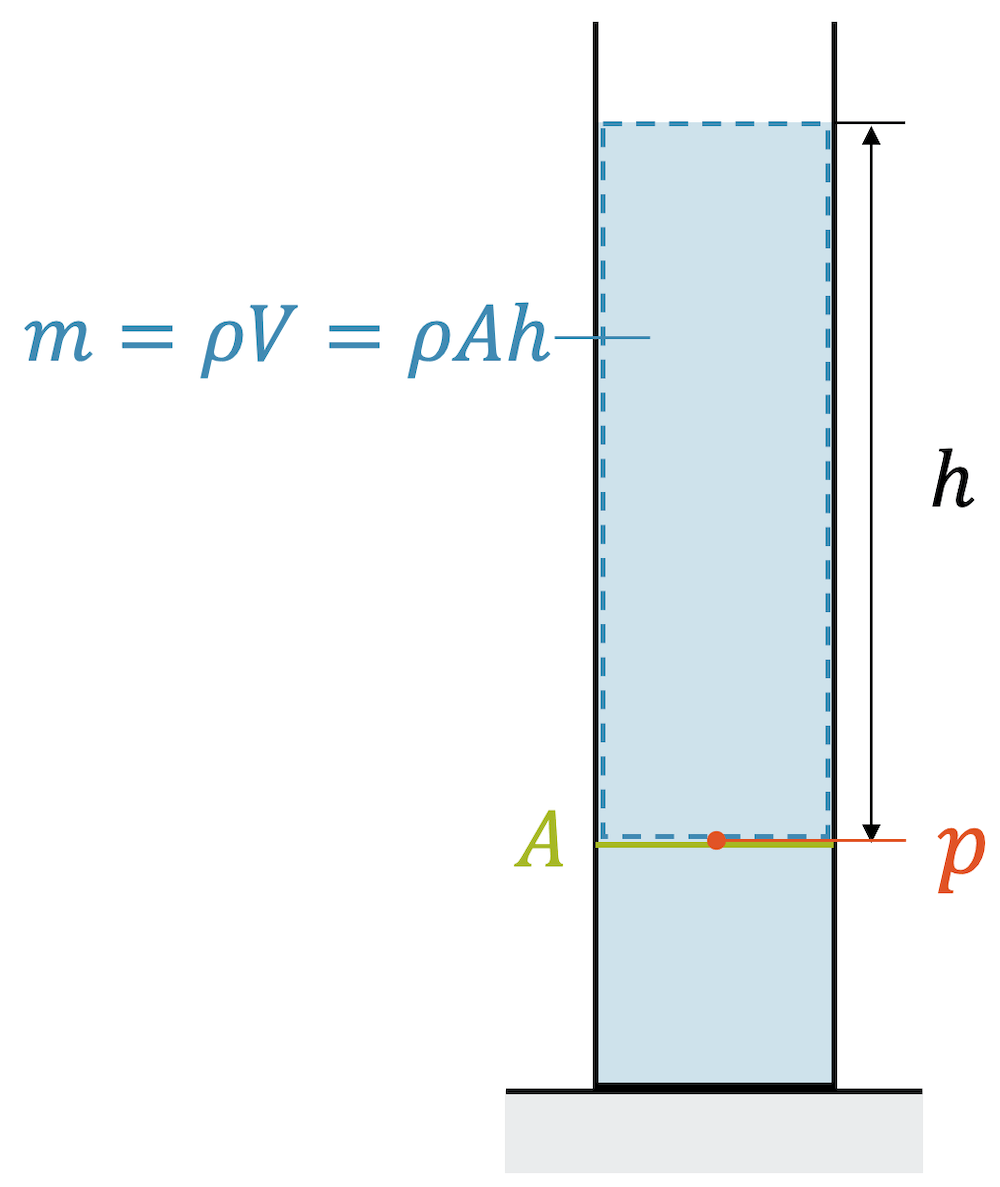
Die Wassersäule über dem betrachteten Punkt hat die Masse \(m\), die mit ihrer Gewichtskraft \(F_g\) auf die Querschnittsfläche \(A\) des Behälters drückt. Für den Druck haben wir also:
\[ p = \frac{F_g}{A} = \frac{mg}{A} \]
Die Masse \(m\) können wir auch mit dem Volumen der Wassersäule \(V\) und der Dichte von Wasser \(\rho\) ausdrücken:
\[ m = \rho \cdot V = \rho \cdot (Ah) \]
Wir setzen diesen Ausdruck oben für \(m\) ein und kürzen die Fläche \(A\) heraus:
\[ \require{cancel} p = \frac{\rho \cdot (\cancel{A}h) \cdot g}{\cancel{A}} \]
Damit erhalten wir einen Ausdruck für den Schweredruck \(p\), der durch eine Wassersäule der Höhe \(h\) über dem betrachteten Punkt erzeugt wird:
\[ p = \rho g h \]
Meistens haben wir über der Flüssigkeitsoberfläche auch noch den Luftdruck bzw. Umgebungsdruck \(p_U\). Das ist gewissermassen ein Stapel von Luftteilchen, der auch ein Eigengewicht hat und somit zu einem eigenen Schweredruck führt. Wir addieren einfach die beiden Drücke und erhalten für den totalen Druck:
\[ p = \rho g h + p_U \]
“Nur ein bisschen Wein hinzu…und die dünne Flüssigkeitssäule sprengte das Fass!” 👀
Pascals Fassversuch
Blaise Pascal (1623 – 1662) war ein französischer Mathematiker und Physiker. Nach ihm ist die Einheit des Drucks benannt.
Im Jahr 1648 führte er sein berühmtes Experiment durch: Er stellte ein mit Wasser gefülltes Holzfass auf. Das Fass war einwandfrei und wasserdicht. An das Fass angebracht war ein langes, dünnes Rohr, das senkrecht aus dem Fass bis zum zweiten Stock eines Hauses reichte.
Er füllte über das dünne Rohr das Fass immer mehr auf, so dass der Wasserspiegel anfing das Rohr hinauf zu klettern. Am Schluss füllte er demonstrativ nur ein bisschen Wein in das Rohr und brachte das Fass unten zum Bersten! 💥

Mit seinem Versuch zeigte er auf eindrückliche Weise, dass er nur mit der Höhe der Wassersäule alleine, einen so hohen Druck im Fass erreichen konnte, welches das Fass zum Bersten brachte.
Dieser Druck braucht gar keine grosse Wassermenge, wie wir uns das aus Intuition vorstellen würden. Allein die Wasserhöhe einer dünnen Säule reicht aus. Die Querschnittsfläche \(A\) hat für den Schweredruck keinen Einfluss!
Hydrostatisches Paradoxon
Pascals Fassversuch zeigte eindrücklich, wie der Schweredruck \(p\) nur von der Höhe, nicht aber von der Querschnittfläche des Gefässes abhängt.
Wir können verschieden geformte Gefässe nebeneinander aufstellen und unten alle mit einem Rohr verbinden. Der Druck unterhalb der Wasserstände muss überall gleich sein, denn ein Druckunterschied würde sich sofort ausgleichen.
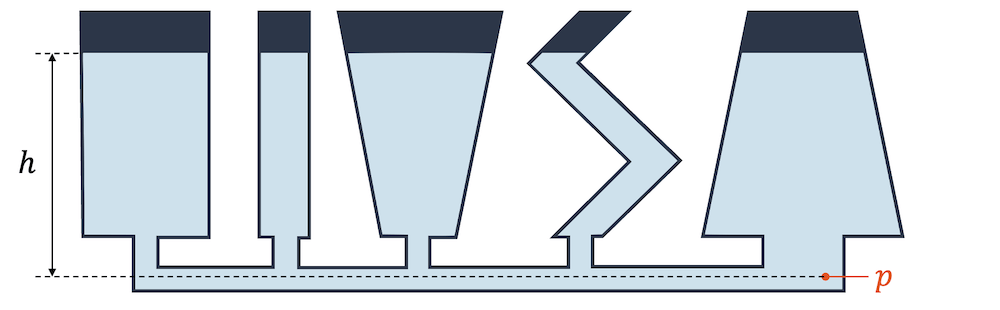
Wir hätten erwartet, dass das Gefäss mit mehr Wasser auch einen grösseren Druck erzeugt. Das ist aber nicht so. Alle Gefäss haben den gleichen Wasserstand!
Jedes Gefäss erreicht den gleichen Druck \(p\), indem es den gleichen Füllstand zulässt. Wird einem Gefäss etwas mehr Wasser beigegeben, so entsteht kurzzeitig ein höherer Druck durch die höhere Wassersäule. Dieser Druck gleicht sich aber aus, indem das Wasser über die Rohrverbindung zu den anderen Gefässen fliesst. Dieses Mal werden die anderen Gefäss von unten aufgefüllt, bis sie alle wieder die gleich hohe Wassersäule erreichen.
“Tiere mit sehr langen Hälsen haben einen kleinen Kopf – eine direkte Folge des Schweredrucks!” 🦕
Anwendungen
Welches Tier hat den grössten Blutdruck? Wenn du jetzt sagst: “Das Tier mit dem grössten Herzen”, dann hast du natürlich recht!
Die Giraffe ist das Tier mit dem stärksten Herzen und dem grösssten Blutdruck. Dieser ist aber nötig, wie wir im folgenden Bild schön sehen können.

Das Gehirn braucht Sauerstoff und das wird mit dem Blut nach oben gepumpt. Weil im Fall der Giraffe der Kopf viel weiter oben ist, als das Herz, muss das Herz auch noch diesen grossen Schweredruck “überwinden”. Deshalb ist das Herz der Giraffe besonders gross und stark gebaut. Gleichzeitig ist das Gehirn des Tiers eher klein, damit der Sauerstoffbedarf möglichst minimal bleibt.
Bei einer Staumauer wird sehr viel Wasser zurückgehalten – entsprechend stark gebaut muss sie sein.
Wir wissen jetzt aber, dass der Druck des Wassers auf die Staumauer nur von der Höhe abhängig ist und nicht von der Breite der Wassersäule. Mit anderen Worten: Es ist unwichtig, wie gross der Stausee ist. Der See könnte z.B. nur einen Meter breit sein und die Mauer müsste trotzdem genauso stark gebaut sein! Verrückt, nicht? 😝

Wir wissen auch, dass die Staumauer ganz unten am meisten belastet ist, ganz oben am wenigsten.
Blieben wir noch schnell bei der Wasserkraft: Mit Speicherseen in den Bergen oben haben wir eine Wassersäule, die manchmal Hunderte von Metern Höhe hat. Der Schweredruck unten im Tal, wo das Kraftwerk steht, ist enorm!
Wir haben Wasser mit sehr hohem Druck zur Verfügung. Dazu werden die sog. Pelton-Turbinen eingesetzt. Oben in der Halle sehen wir die Generatoren, die von der Turbine angetrieben werden.

Image by Kecko, https://www.flickr.com/photos/kecko/34103743646/in/photostream/, CC BY 2.0
Darunter liegt die Pelton-Turbine, die von mehreren Düsen angetrieben wird.

Image by Kecko, https://www.flickr.com/photos/kecko/34103743646/in/photostream/, CC BY 2.0
Diese Monster von Turbinen haben immer eine Doppelschale, die den Wasserstrahl auffangen und oben und unten zurückwerfen.

Image by Kecko, https://www.flickr.com/photos/kecko/34103743646/in/photostream/, CC BY 2.0
Aufgabensammlung
Lernziele
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.