Inhalt
Das Wichtigste in Kürze
Wenn wir zwei Festkörper zusammendrücken, entsteht an ihrer Grenzfläche \(A\) ein Druck \(p\), den wir in diesem Fall Auflagedruck nennen. Er entspricht der Kraft \(F\) pro Fläche \(A\):
\[ p = \frac{F}{A} \]
Grosse Auflagedrücke erreichen wir mit einer grossen Kraft oder typischerweise mit einer sehr kleinen Fläche.
Videos
Häufigste Fragen
“Teilchen, die diese elektromagnetische Kraft nicht spüren (z.B. Neutrinos), fliegen durch unsere Hand oder Wand, wie ein Flugzeug durch eine Wolke!”
Was passiert, wenn zwei Flächen sich berühren?
Wenn wir z.B. mit der flachen Hand gegen die Wand drücken, so reagiert die Wand mit einer Normalkraft, die dagegen wirkt. Je stärker wir drücken, desto grösser ist der Druck.
Ich möchte Dir nachfolgend eine Modellvorstellung geben, die zwar bewusst nicht stimmt, aber das Bild der Realität klarer macht:
Irgendwie treffen die beiden Materialien aufeinander und wir spüren die harte Wand. Was passiert da genau?
Material besteht aus Molekülen oder Atomen, die je von einer grossen Elektronenwolke umgeben sind. Ich sage gross, weil seit dem Experiment von Rutherford wissen wir, dass der Kern so unglaublich viel kleiner ist, als das Atom selbst.
Wir zwingen jetzt gewissermassen die Atome der Hand in die Atome der Wand hinein, so dass deren Elektronenwolken aufeinander stossen. Stell Dir vor, eine richtige Wolke kommt von oben und drückt auf die Wolkendecke unten. ☁️

Image by Emmanuel Appiah, shared on Unsplash
Wir wissen ja: Es ist leider nicht möglich, auf einer Wolke zu liegen! Wir würden durch die Wolke fallen. Deshalb würden sich zwei Wolken ohne Probleme durchdringen.
Wie erklären wir den “harten Widerstand” der Wand? Mit der Hand können wir nicht in die Wand hineingreifen, weil sich die Elektronenwolken von Hand und Wand gegenseitig mit der sog. Coulombkraft abstossen.
Hätten die richtigen Wolken auch so eine Kraft, dann wäre die Wolkendecke für eine andere Wolke eine harte Fläche.
Für andere Objekte, die diese Kraft nicht kennen, wäre alles beim Alten. Ein Flugzeug würde z.b. diese “Wolkenkraft” nicht kennen und könnte ungehindert durch eine Wolke fliegen. In Wirklichkeit können kleinste Teilchen (z.B. Neutrinos) durch unsere Hand oder durch die Wand fliegen. Weil dort gar nichts ist, ausser Elektronenwolke!
“Die Wand ist nicht hart, weil ‘dort etwas ist’, sondern weil sich die Elektronenwolken mit der Coulombkraft abstossen.”
Einfluss der Grösse der Fläche
Die Coulombkraft nimmt umso mehr zu, je mehr sich die Elektronenhüllen, durch äusseren Zwang, durchdringen müssen. Die Reaktion darauf ist die abstossende Kraft, die wir bislang als Normalkraft bezeichnet hatten.
Im nachfolgenden Bild sehen wir wie ein “blauer Feststoff” auf eine rote Unterlage drückt. Die Atomkerne sind als Punkte dargestellt, die Elektronenwolken als halb-transparente Kreise. Wir sehen, dass sie sich bei Druck leicht überlappen können.
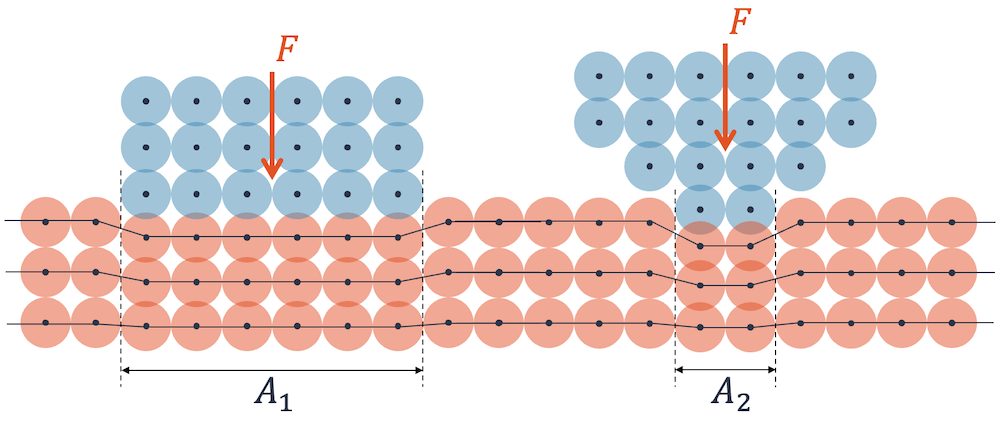
In beiden Fällen wirkt die gleiche Kraft \(F\). Links wird sie über eine grosse Fläche \(A_1\) verteilt. Rechts ist die gleiche Kraft auf eine kleinere Fläche \(A_2\) konzentriert.
Wir sehen, dass links mehr Elektronenhüllen beteiligt sind und sie die Kraft untereinander besser aufteilen.
Bei einer kleineren Fläche \(A_2\) übernimmt die einzelne Elektronenhülle mehr Kraft und muss auch mehr Überlappung erdulden.
Da die Anzahl beteiligter Elektronenhüllen proportional zur Kontaktfläche ist, können wir für die Belastung des Materials die drückende Kraft durch die Kontaktfläche teilen. Diese neue Grösse heisst Auflagedruck:
\[ p = \frac{F}{A} \]
Wie berechnet man den Auflagedruck?
Wenn wir zwei Festkörper zusammendrücken, entsteht an ihrer Grenzfläche ein Druck, den wir in diesem Fall Auflagedruck nennen.
Der Auflagedruck \(p\) berechnet sich aus der Kraft \(F\), mit welcher zwei Flächen \(A\) aufeinander drücken:
\[ p = \frac{F}{A} \]
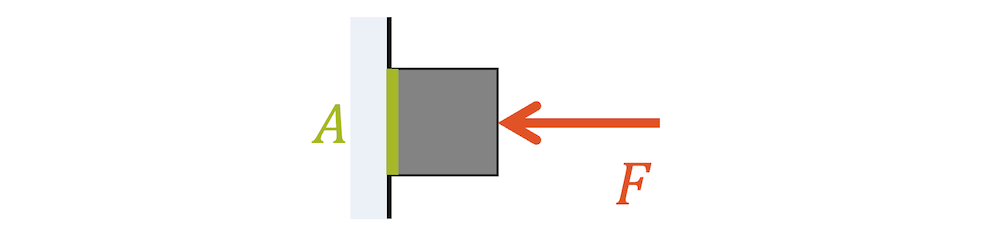
Der Auflagedruck ist so etwas wie die ‘Kraftdichte’, d.h. wie stark die Kraft durch auf einer Fläche verteilt (kleiner Auflagedruck) oder wie stark sie auf eine kleine Fläche ‘aufkonzentriert’ ist (grosser Auflagedruck).
Die Einheit des Auflagedrucks ist Pascal (Pa), benannt nach Blaise Pascal (1623-1662), dem französischen Mathematiker und Physiker.
\[ [\,p\,] = \frac{\text{N}}{\text{m}^2} = \text{Pa} \]
In der Kontinuumsmechanik, d.h. in der Lehre der Belastungen und Deformationen von Materialien, spricht man nicht von Auflagedruck, sondern von der Druckspannung \(\sigma\) im Material:
\[ \sigma = \frac{F}{A} \]
Hat der Auflagedruck eine Richtung?
Das ist eine knifflige Frage!
Die Kraft hat ganz klar eine Richtung und wird in der Physik deshalb auch mit einem Vektor beschrieben, der einen Betrag hat (Länge des Pfeils) und eine Richtung.
Etwas weniger offensichtlich ist aber, dass die Kontaktfläche, wo der Auflagedruck entsteht, eine Richtung hat. Wir können sie mit dem Lot auf die Fläche angeben.
Weil wir beim Druck aber festgehalten haben, dass er grundsätzlich keine Richtung hat und auch kein Vektor ist, beantworte ich diese Frage mit einem nein. Der Auflagedruck hat keine Richtung. 🙂
Beachte, dass die verwandte Grösse Druckspannung eine Richtung hat.
Grosse und kleine Auflagedrucke
In der Formel für den Auflagedruck erkennen wir, dass wir einen hohen Auflagedruck erreichen…
- mit einer sehr grossen Kraft
- mit einer sehr kleinen Fläche
Wenn wir uns z.B. auf einen zugefrorenen See wagen, können wir das Risiko des Einbrechens reduzieren, wenn wir unsere Gewichtskraft auf eine möglichst grosse Fläche verteilen. Das erreichen wir im Liegen oder wenn wir auf einem Brett stehen, das die Krafteinleitung ins Eis verteilt.
Wollen wir aber ein Loch ins Eis bohren, ist es gerade umgekehrt: Wir wählen einen möglichst spitzen Bohrer, der mit seiner kleinen Fläche das darunter liegende Eis aufbrechen kann.

© by Riccardo, https://www.pexels.com/photo/two-person-wearing-shoes-in-front-of-each-other-300875/, CC0
Aus physikalischer Sicht nicht zu empfehlen wäre das Tragen von Schlittschuhen mit dünnen Kufen ⛸️ oder Schuhen mit hohen Absätzen. Diese leiten die Gewichtskraft über eine sehr kleine Fläche in den Boden und würden deshalb am ehesten sich ins Eis hineinbohren.

© by Castorly Stock, https://www.pexels.com/photo/red-leather-peep-toe-heeled-sandals-3682292/, CC0
Die nachfolgende historische Aufnahme eines Fakirs zeigt ihn auf dem Nagelbrett. Die Gewichtskraft wird auch hier über sehr kleine Flächen übertragen, so dass hohe Auflagedrücke entstehen.

Viel bequemer wäre das weiche Sofa im nächsten Bild! Hier wird die Gewichtskraft über eine maximale Fläche verteilt, so dass wir kaum einen Auflagedruck mehr spüren.

Die Weltmeister des Auflagedrucks sind Nadeln und Messerklingen. Sie arbeiten beide mit der Wirkung von extrem kleinen Flächen. Die Kontaktfläche ist so klein, dass der hohe Auflagedruck das darunter liegende Material leicht durchdringen kann. 😫
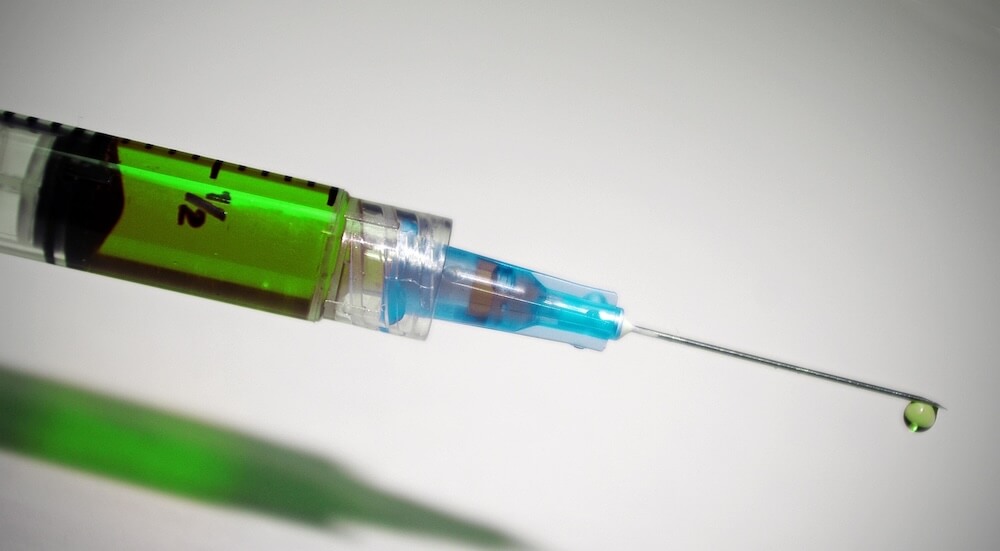
Beispiel
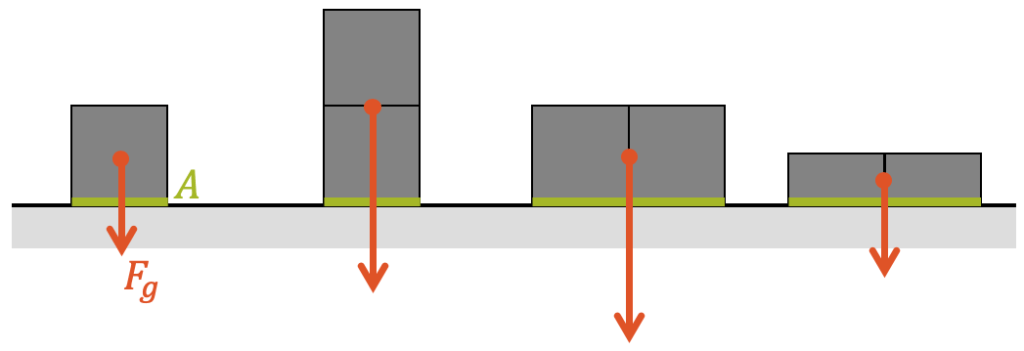
Beispiel
Aufgabensammlung
Lernziele
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt









Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.