Kinetische Energie (Bewegungsenergie)

Die kinetische Energie ist in der Geschwindigkeit von Masse begründet. Es gibt auch hier verschiedene Varianten von kinetischen Energien: Ein Meteorit hat sehr viel kinetische Energie, die auf der Erde grosse Zerstörung anrichten könnte. Im Kleinsten haben Atome oder Moleküle diese Energie, denn sie bewegen sich schnell, was wir als thermische Energie kennen.

Kinetische Energie Definition

Kinetische Energie Symbol: \(E_{\text{kin}}\) (manchmal auch \(T\))

Kinetische Energie Einheit: \(\text{J}\) (Joule, übliche Einheit der Energie)

Kinetische Energie Formel (Herleitung)

Wir schauen uns ein Beispiel an: Eine Radfahrerin beschleunigt von 5 km/h auf 25 km/h. Das braucht erfahrungsgemäss ein bisschen Kraft. Diese Kraft wirkt über eine bestimmte Beschleunigungsstrecke, d.h. wir haben Kraft und Weg: die Radfahrerin muss physikalische Arbeit verrichten.

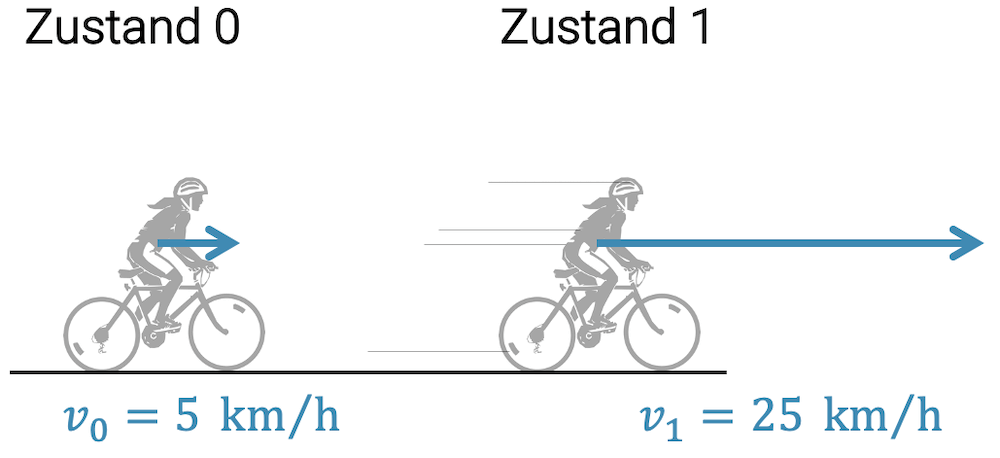
Diese Arbeit ist Beschleunigungsarbeit und was sich ändert, ist die Geschwindigkeit, d.h. die Radfahrerin hat nachher mehr kinetische Energie als vorher.

Die Energie, die sie im Zustand 0 hatte (vor der Beschleunigung) ändert um den Betrag der Arbeit \(W\) in den Zustand 1, den sie nach der Beschleunigung einnimmt. Die Arbeit ist die Energie, die dazu gekommen ist:

\[ W = \Delta E = E_{\text{kin},1} – E_{\text{kin},0} \]

Jetzt nehmen wir die Formel für die Beschleunigungsarbeit:

\[ W = \frac{1}{2} m v_1^2 – \frac{1}{2} m v_0^2 \]

Der Vergleich der beiden Formeln gibt uns die Formel für kinetische Energie, denn der erste Summand beschreibt den Zustand 1 und der zweite Summand den Zustand 0:

\[ E_{\text{kin},1} = \frac{1}{2} m v_1^2, \qquad E_{\text{kin},0} = \frac{1}{2} m v_0^2 \]

Egal welcher Zustand: Die Formel der kinetischen Energie ist:

\[ E_{\text{kin}} = \frac{1}{2} m v^2 \]

Mit der Masse \(m\) und der Geschwindigkeit \(v\) lässt sich die kinetische Energie berechnen, von jedem Zustand. In unserem Beispiel:

\[ E_{\text{kin},1} = \frac{1}{2} \cdot 75\,\text{kg} \cdot \Big(\frac{25}{3.6} \, \frac{\text{km}}{\text{h}}\Big)^2 \]

Nach der Beschleunigung hat die Radfahrerin (zusammen, mit ihrem Fahrrad) folgende Menge an Bewegungsenergie gespeichert:

\[ E_{\text{kin},1} = 1’808\,\text{J} \]

Möchte sie voll abbremsen, so muss sie diese Menge an Energie wieder mit Reibungsarbeit an den Bremsen abbauen.

Beachte, dass die Geschwindigkeit \(v\) in der Formel immer relativ zu einem willkürlich gewählten Referenzsystem gemessen wird. Für die meisten Geschwindigkeiten wird die “ruhende” Erde als Referenzsystem gewählt, d.h. die Geschwindigkeit ist im Vergleich zur Erde.

Ebenfalls zu beachten ist, dass die kinetische Energie wegen des Quadrats in der Formel nie negativ sein kann.

Kinetische Energie und potentielle Energie

Wenn die kinetische und die potenzielle Energien die beiden wichtigsten Energieformen darstellen, sind die meisten Phänomene auf ein Zusammenspiel dieser beiden Energieformen zurückzuführen. Am einfachsten verständlich ist dies wiederum am Beispiel der Radfahrerin:

Sie lässt sich oben am Hügel aus dem Stand heraus hinunterrollen. Oben, im Zustand 0, hat sie potenzielle Energie. Beim Runterfahren verringert sie die Höhe und verliert damit potenzielle Energie.

Die Energie geht aber nicht wirklich verloren, sondern wird in kinetische Energie umgewandelt. Wie schnell kann unsere Radfahrerin dabei werden?

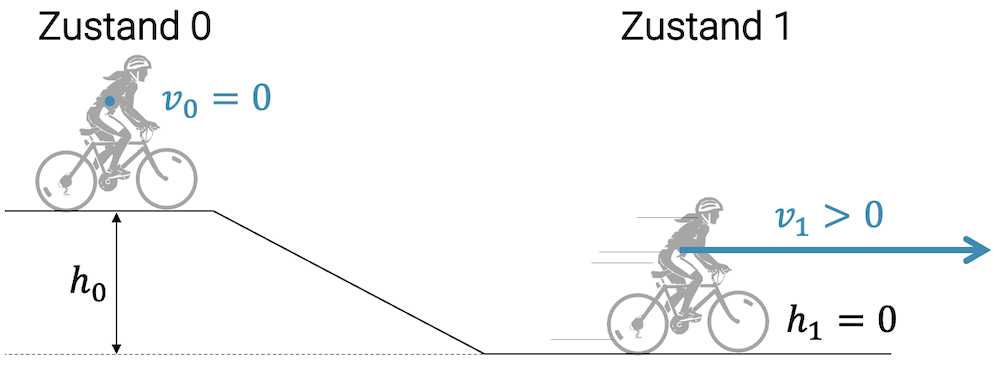
Wir nehmen die potenzielle Energie, die sie im Zustand 0 hat:

\[ E_{\text{pot},0} = mgh_0 \]

Unten hat sie nur noch:

\[ E_{\text{pot},1} = mgh_1 \]

Die Energiemenge, die sie von oben nach unten abgegeben hat, ist die Differenz:

\[ E_{\text{pot},0} – E_{\text{pot},1} \]

\[ mgh_0 – mgh_1 = mg \cdot (h_1 – h_0) \]

Machen wir ein Zahlenbeispiel: Sie war auf der Höhe 100 m und ist auf die Höhe 20 m runter gefahren. Wir setzen diese Zahlen oben ein:

\[ 75\,\text{kg} \cdot 9.81\,\frac{\text{m}}{\text{s}^2} \cdot \big(100\,\text{m} – 20\,\text{m}\big) = 58’860\,\text{J} \]

Diese ganze Energie hat die Radfahrerin als potenzielle Energie verloren, d.h. sie wurde in kinetische Energie umgewandelt.

Wir wissen jetzt, wie viel kinetische Energie sie hat, denn am Anfang, stand sie still (keine kinetische Energie) und jetzt hat sie 58’860 J aus potenzieller Energie erhalten.

Um daraus die Geschwindigkeit zu berechnen, müssen wir die kinetische Energie Formel umstellen:

\[ E_{\text{kin}} = \frac{1}{2} m v^2 \quad \rightarrow \quad v = \sqrt{\frac{2 E_{\text{kin}}}{m}} \]

Wir setzen ein:

\[ v = \sqrt{\frac{2 \cdot 58’860\,\text{J}}{75\,\text{kg}}} = 39.6\,\frac{\text{m}}{\text{s}} = 142.6\,\frac{\text{km}}{\text{h}} \]

Wow! Kann das sein?

Ja, das ist richtig, nur haben wir keinerlei Reibung berücksichtigt und das ist leider unrealistisch. Selbst wenn sie nicht bremst, gibt es viel Luftwiderstand und auch Rollreibung, Reibung in den Radlagern etc.

Die umgekehrte Umwandlung ist auch möglich: Nämlich der Fall, in welchem die Radfahrerin den Hang hochfährt, ohne in die Pedale zu treten. Sie nutzt ihre kinetische Energie aus.

Je weiter oben sie auf der Rampe ist, desto mehr potenzielle Energie hat sie aufgebaut. Diese potenzielle Energie kommt aber nicht aus dem nichts, sondern wurde mit Abbau von kinetischer Energie bezahlt.

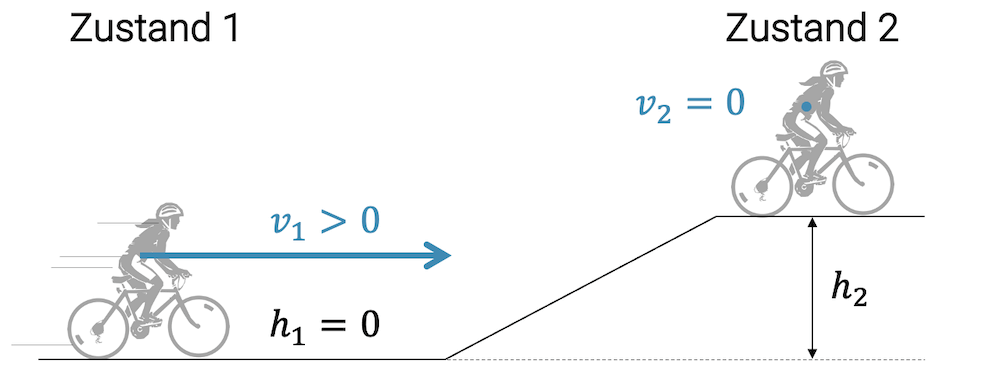
Wie hoch kann sie kommen mit 58’860 J an Bewegungsenergie?

Da die Menge an potenzieller Energie höchstens so gross werden kann, wie die Radfahrerin anfangs in Form von kinetischer Energie hatte, können wir schreiben:

\[ E_{\text{pot},2} = E_{\text{kin},1} \]

\[ mgh_2 \;\; = \;\; E_{\text{kin},1} \]

Um die Höhe zu kriegen, dividieren wir durch \(m\) und \(g\) und setzen ein:

\[ h_2 = \frac{E_{\text{kin},1}}{mg} = \frac{58’860\,\text{J}}{75\,\text{kg}\cdot 9.81\frac{\text{m}}{\text{s}^2}} = 80\,\text{m} \]

Das sollte uns nicht überraschen!

Mit dieser Energie kann sie wieder 80 m Höhe gewinnen. In der Realität erreicht sie wegen der Reibung nur einen Bruchteil der Geschwindigkeit, die wir berechnet haben. Damit hat sie auch nur einen Bruchteil der kinetischen Energie und darf deshalb für den Rest der potenziellen Energie dann doch in die Pedale treten!

Kinetische Energie Beispiele

Im weiteren schauen wir uns Bewegungsenergie Beispiele an, meistens kombiniert mit der Lageenergie (potentielle Energie).

Die Achterbahn ist ein gutes Beispiel, denn die Wagen haben selber keinen Antrieb. Der Antrieb befindet sich an der Rampe, wo die Wagen auf ihre maximale Höhe gebracht werden. Dieser Antrieb verrichtet die Hubarbeit und speichert die Energie in Form von potentieller Energie in den Wagen (und den Leuten).

Ab da rollen die Wagen runter, erreichen eine hohe kinetische Energie und bauen diese bei der nächsten Auffahrt wieder zugunsten von potentieller Energie ab, bevor es wieder runter geht.

Auf der Kinderschaukel haben wir das gleiche Wechselspiel zwischen potentieller und kinetischer Energie: Beim Start hat das Kind potentielle Energie.

Im tiefsten Punkt ist diese potentielle Energie in kinetische Energie umgewandelt.

Mit dem “Schuss” geht es wieder hinauf, die kinetische Energie wird wieder abgebaut und in potentielle Energie umgewandelt, bis das Kind am Wendepunkt kurz in Ruhe ist.

Das Kind muss zwischendrin angeben, um die Reibungseffekte zu kompensieren. Ohne Reibung könnte das Kind ununterbrochen schaukeln.

Pendel funktionieren gleich, wie die Schaukel. Was sie letztlich abklingen lässt, ist die Reibung. Ansonsten könnten sie die anfänglich eingesetzte potenzielle Energie beliebig oft in kinetische Energie umwandeln und wieder umgekehrt.

Die Eisenbahn nutzt die kinetische Energie auf sehr effiziente Weise: Da Eisenbahnen eine sehr grosse Masse haben, ist die Menge an kinetischer Energie bei der Eisenbahn entsprechend gross.

Auf einer horizontalen oder unmerkbar abschüssigen Strecke kann die Eisenbahn einfach rollen lassen. Die Fahrgäste merken nicht, dass sie minutenlang ganz ohne Antrieb fahren!

Andere Beispiele für Bewegungsenergie verknüpfen die kinetische Energie mit der Reibungsarbeit.

Wenn ein Auto plötzlich eine Vollbremsung machen muss, bedeutet das aus energetischer Sicht, dass die Geschwindigkeit vollständig abgebaut werden muss und zwar so schnell wie möglich. Das bedeutet auch, dass die kinetische Energie weg muss!

Mit Hilfe der Bremsen können wir diese kinetische Energie mit Reibungsarbeit abbauen und in thermische Energie umwandeln. Eigentlich beschleunigen wir damit die Teilchen in den Bremsscheiben, deren Temperatur steigt. Da aber die Teilchenbewegung insgesamt ungerichtet ist, wird die Bremsscheibe nicht schneller, sondern nur heisser.

Weitere Beispiele:

• Atome oder Moleküle eines Gases
• kosmische Teilchen
• Menschen, die rennen, springen etc. aber auch z.B. die Bewegung der Arme, Beine etc.
• Flüssigkeiten, z.B. der Wasserstrahl, der aus dem Feuerwehrschlauch austritt
• Fahrzeuge, Flugzeuge
• Geschosse
• Asteroiden, Kometen, Meteoriten etc.

Kinetische Energie starrer Körper (Rotationsenergie)

Bis hierher haben wir immer Objekte bewegt. Die ganze Masse dieser Objekte kann auch in ihrem Schwerpunkt S konzentriert werden, d.h. wir haben Fälle betrachtet, in welchen ein Schwerpunkt mit Geschwindigkeit \(v\) sich bewegt.

Beispielsweise fliegt ein Wasserstoffmolekül mit der Geschwindigkeit \(v\) im Vakuum.

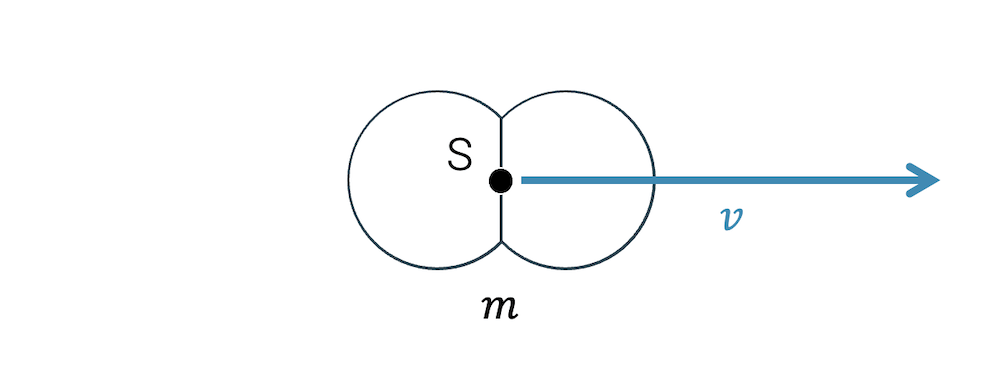
Dieses Wasserstoffmolekül könnte aber auch um den Schwerpunkt herum rotieren. Das wäre zusätzliche Bewegung, die unabhängig ist von der Bewegung des Schwerpunkts. Selbst ein ruhendes Wasserstoffatom könnte so kinetische Energie haben, rein durch die Rotation gegeben.

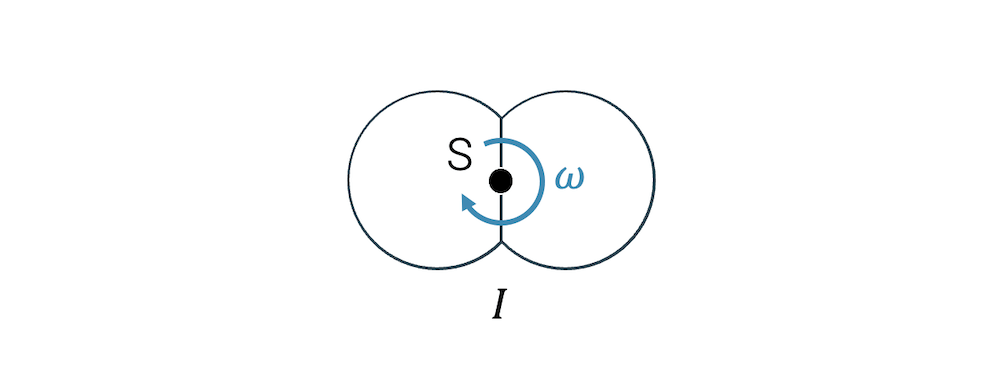
Diese Form der kinetischen Energie wird Rotationsenergie genannt.

Wäre die ganze Masse eines solchen Wasserstoffmoleküls tatsächlich in einem Schwerpunkt konzentriert, wäre eine Rotation gar nicht möglich: Ein unendlich kleiner Punkt ohne Ausdehnung kann gar nicht rotieren bzw. wir können das ja nicht feststellen.

Das Wasserstoffmolekül ist aber mehr eine Art Hantel und die beiden Atome haben ihre Masse und sie bewegen sich auf einer Kreisbahn um den Schwerpunkt herum.

Beschränken wir uns vorerst auf eine einzelne rotierende Masse \(m\), die im Abstand \(r\) um das Zentrum kreist.

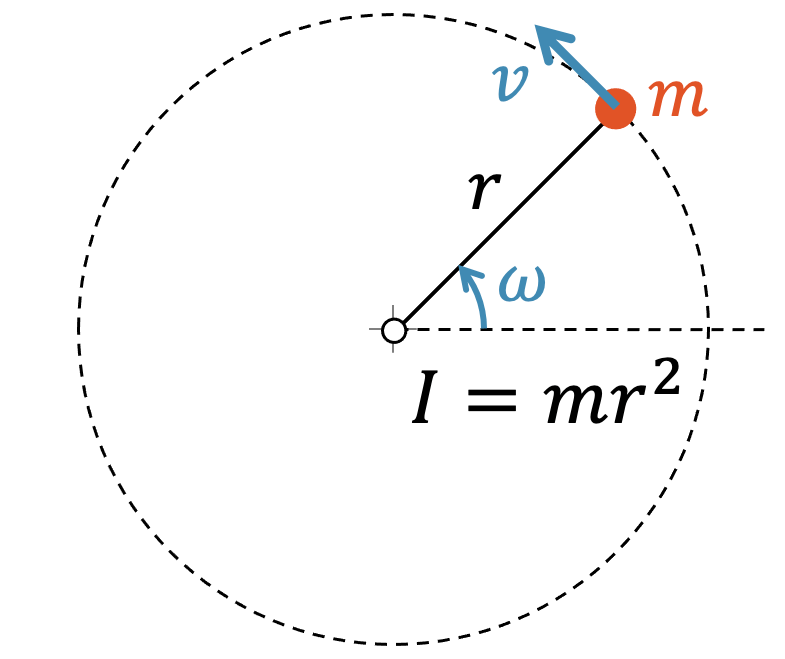
Diese Masse hat ganz klar kinetische Energie, denn die Masse hat eine Bahngeschwindigkeit \(v\). Die translatorische kinetische Energie wäre demnach:

\[ E_{\text{kin}} = \frac{1}{2} m v^2 \]

Wir können die Bahngeschwindigkeit als Funktion der Winkelgeschwindigkeit \(\omega\) ausdrücken:

\[ v = r \cdot \omega \]

Oben eingesetzt, erhalten wir:

\[ E_{\text{kin}} = \frac{1}{2} \cdot m \cdot (r \omega)^2 = \frac{1}{2} \cdot (mr^2) \cdot \omega^2 \]

Der Ausdruck in der Klammer \((mr^2)\) entspricht dem Trägheitsmoment \(I\) eines Massepunkts, der sich auf einer Kreisbahn mit Abstand \(r\) bewegt bzw. dessen Drehachse den Abstand \(r\) hat. Wir erhalten so die Formel für die Rotationsenergie:

\[ E_{\text{kin}} = E_{\text{rot}} = \frac{1}{2} \cdot I \cdot \omega^2 \]

Zurück zu unserem Wasserstoffmolekül. Für eine Hantel müsste man in Tabellen das Trägheitsmoment \(I\) für ein solches Gebilde suchen. Einfacher ist das Zusammensetzen des Moleküls aus zwei einzelnen Massepunkten der Masse \(m\) mit dem jeweiligen Abstand \(\delta\) vom gemeinsamen Zentrum:

\[ I = I_1 + I_2 = m\delta^2 + m\delta^2 = 2m\delta^2 \]

Ist der Körper nicht starr, so könnte eine weitere Bewegungsform kinetische Energie speichern: die Oszillation (Schwingung). Die beiden Atome im Wasserstoffmolekül könnten sich annähern und sich dann wieder von einander entfernen.

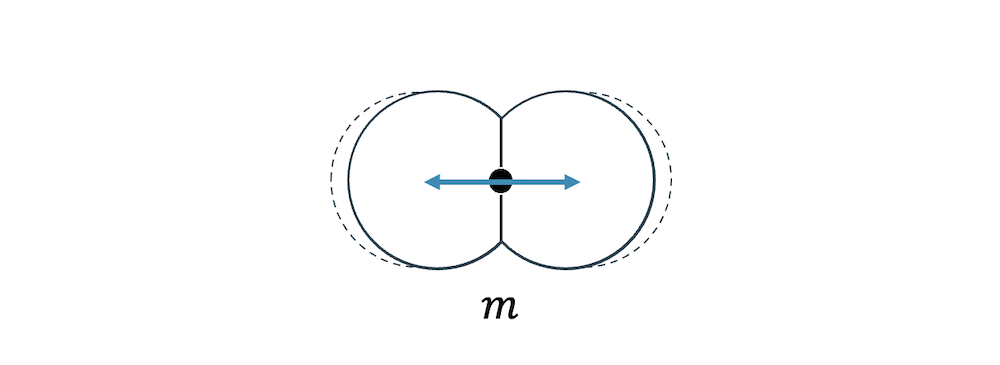
Diese Bewegung ist keine Bewegung des Schwerpunkts und sie stellt auch keine Rotation dar, denn die Winkelgeschwindigkeit ist null. Es ist eine neue, zusätzliche Bewegungsform. Man sagt dem auch ein weitere Freiheitsgrad.