Wirkungsgrad

Bei den meisten Geräten oder Maschinen werden Energien umgewandelt. Wegen der Energieerhaltung geht niemals Energie verloren, jedoch entstehen oft auch ungewollte Energieformen (z.B. Wärme durch Reibung). Diese unnützen Energieformen entsprechen nicht dem ursprünglichen Zweck und werden deshalb als “Verlust” angesehen. Der Wirkungsgrad \(\eta\) vergleicht, wie viel der eingesetzten Energie \(\Delta E_{in}\) in Energie in nützlicher Form \(\Delta E_{out}\) umgewandelt worden ist. Werden Energieströme betrachtet, d.h. Energiemengen pro Zeit, so vergleicht man die eingesetzte Leistung \(P_{in}\) mit der gewonnenen, nützlichen Leistung \(P_{out}\):

\[ \eta = \frac{\Delta E_{out}}{\Delta E_{in}} = \frac{P_{out}}{P_{in}} \]

Der Wirkungsgrad ist keine Grösse der physikalischen Natur. Sie beinhaltet eine menschliche Wertung der Energieformen in “nützlich” und “unnütz”. Ohne diese Wertung hätten wir für sämtliche Prozesse immer die Energieerhaltung und damit einen Wirkungsgrad von exakt \(\eta = 1\).

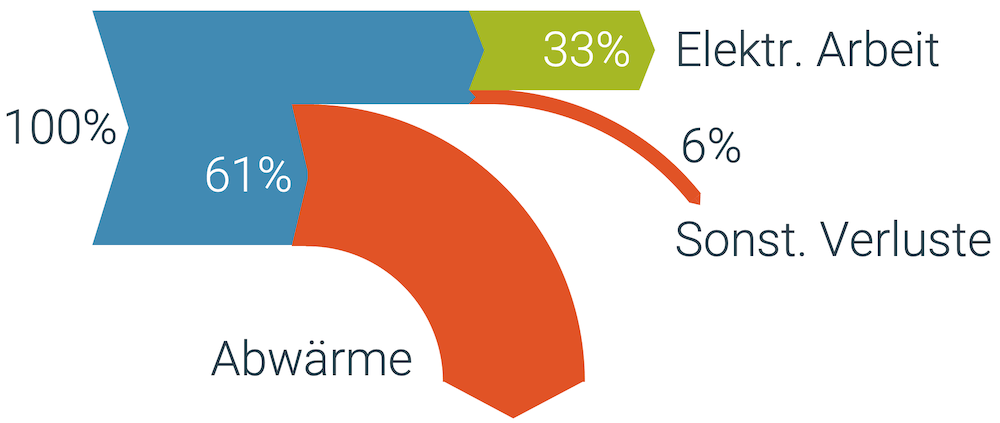
Der Wirkungsgrad kann in einem Sankey-Diagramm auch grafisch dargestellt werden: Der Fluss der nützlichen Energieform steht im Vergleich zum Fluss der eintretenden Energieform (Input). Je grösser der Anteil der austretenden nützlichen Energie im Vergleich zum Input ist, desto grösser ist der Wirkungsgrad \(\eta\).

Definitionen

Abkürzung: \(\eta\) (griechisches “eta”)

Einheiten: \([\eta]\) = # (Zahl, keine Einheit)

Wertebereich:

\(\eta = 0\)	Minimaler Wirkungsgrad
\(0 < \eta < 1\)	Realer Wirkungsgrad
\(\eta = 1\)	Theoretischer (idealer) Wirkungsgrad
\(\eta > 1\)	Spezialfälle (siehe unten) oder Perpetuum-Mobile (erster Art)

In einem theoretischen Fall können 100% der eingesetzten Energie in die nützliche Energieform umgewandelt werden. Wir erhalten so \(\eta\) = 1 = 100%. Im anderen Extremfall kriegen wir gar keine Umwandlung hin, sondern verlieren die ganze Energie an eine unnütze Energieform. Wenn der nützliche Output null ist, verschwindet auch der Wirkungsgrad: \(\eta\) = 0 = 0%.

In reale Prozessen, Maschinen und Geräten gibt es immer gewisse Reibungseffekte, die eine Umwandlung eines Teiles der Energie in Wärme darstellen. Wärme ist, ausser bei Heizungen, meistens keine erwünschte Energieform. Damit verlieren wir in realen Prozessen immer einen Teil der eingesetzten Energie an die (unnütze) Wärme und der Wirkungsgrad ist sicherlich kleiner als 100%.

Beispiel 

Glühbirnen waren früher genau das, was ihr Name sagt: birnenförmige Glaskörper in welchen ein feiner Draht aus Wolfram so stark erhitzt wird, dass er sichtbar glüht. Der Wirkungsgrad dieser Glühbirnen war im einstelligen Prozentbereich, also sehr klein. Der Glühbirne wurden 100% elektrische Energie zugeführt, jedoch kamen nur 5% in Form von Strahlungsenergie (Licht) heraus. Wegen der Energieerhaltung wissen wir, dass die restlichen 95% der Energie nicht verschwunden sind, sondern in Wärme umgewandelt worden sind.

Die heutigen LED-Leuchtkörper sind in der Anschaffung wesentlich teurer als die alten Glühbirnen, aber wesentlich effizienter: Im obigen Beispiel werden 12 W elektrische Energie umgewandelt in 3 W Strahlungsenergie und 9 W Wärme. Damit werden 3 von 12 Watt in die nützliche Form umgewandelt und der Wirkungsgrad beträgt:

\[ \eta = \frac{P_{out}}{P_{in}} = \frac{3\,\mathrm{W}}{12\,\mathrm{W}} = 0.25 = 25\% \]

Auf den ersten Blick erscheint auch dieser Wirkungsgrad nicht besonders gut, denn drei Viertel der Energie werden auch hier zu ungewollter Wärme umgewandelt. Dennoch ist dieser Leuchtkörper fünf mal effizienter als die alte Glühbirne (25% statt 5%). Mit der gleichen Menge an elektrischer Energie können wir eine alte Glühbirne oder fünf neue LED-Leuchtkörper betreiben. Um die Konsumenten zum Umsteigen auf die effizienteren, aber teureren Leuchtkörper zu bewegen, wurden die konventionellen Glühbirnen gesetzlich verboten.

Spezialfälle 

Gibt es Wirkungsgrade, die grösser als 100% sind? Jein, denn die Energieerhaltung verbietet uns das Erschaffen von neuer Energie. Das wäre aber nötig, wenn wir bei einem Wirkungsgrad von mehr als 100% auch mehr Output als Input haben. Es gibt ein paar “buchhalterische” Kunstgriffe mit welchen wir Wirkungsgrade von mehr als 100% erreichen können. Wenn wir unsere Betrachtung auf einen kurzen Zeitbereich beschränken, so können wir Energie aus einem gegebenen Energiespeicher beziehen und ihn somit nicht als Input zählen. Beispiel: Ein Stausee kann in einer Trockenperiode mehr Energie erzeugen, als ihm in Form von Niederschlägen zugeführt worden ist.

Eine weitere Möglichkeit besteht darin, gewisse Energieformen nicht als Input zu zählen, weil sie nichts kosten. Damit ist der Nenner in der Gleichung des Wirkungsgrads zu klein, so dass ein Wert von mehr als 100% erreicht wird. Beispiel: Eine Wärmepumpenheizung nimmt 1 kWh elektrische Energie auf (bezahlter Input) und zusätzlich 3 kWh Wärme aus der Umgebung (gratis Input). Sie wandelt alles zu 4 kWh Heizwärme um (nützlicher Output) und erreicht damit den folgenden Wirkungsgrad:

\[ \eta = \frac{4\,\mathrm{kWh}}{1\,\mathrm{kWh}} = 4 = 400 \% \]

Erhalten wir einen Wirkungsgrad \(\eta > 1\), der nicht zu den oben beschriebenen Spezialfällen gehört und wird tatsächlich immer mehr Energie abgegeben als aufgenommen, d.h. es wird Energie erzeugt, so handelt es sich um eine physikalisch unmögliche Maschine, einem sog. Perpetuum-Mobile (erster Art).

Energieverbrauchskennzeichnung

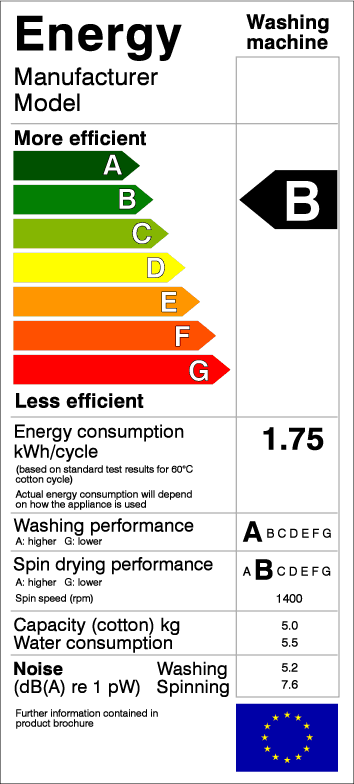
Im Jahre 2010 wurde in der EU die Kennzeichnung von Geräten mit Hilfe eines einheitlichen Labels obligatorisch. Diese Energieverbrauchskennzeichnung ist farblich so gestaltet, dass für den Konsumenten auf einen Blick ersichtlich wird, wie gut der Wirkungsgrad eines Produktes ist. Damit soll die Kaufentscheidung auch aufgrund des Wirkungsgrades beeinflusst werden, der sonst für den Konsumenten nicht bekannt ist.

Die Klasse “A+++” steht für die höchsten Wirkungsgrade, vor “A++” bzw. “A+”, “A”, “B” etc. Die Klasse “G” bildet das Schlusslicht mit den kleinsten Wirkungsgraden. Ein Leuchtkörper, wie im obigen Beispiel mit \(\eta\) = 25%, kommt knapp in die Klasse “B”, wobei mit 24% wäre er noch in die Klasse “A” eingeteilt worden. Das ist für Leuchtkörper ein ziemlich guter Wirkungsgrad.

Nimmt man aber ein Auto mit Wirkungsgrad \(\eta\) = 25%, so wäre es ein “A+++”-Produkt, sogar bis 44%, denn Autos sind nicht so effizient.