Das Wichtigste in Kürze
Das Vektorprodukt (oder auch ‘Kreuzprodukt’ oder ‘äusseres Produkt’ genannt) ist ein Produkt zweier Vektoren, das einen neuen Vektor ergibt, der senkrecht auf den beiden ursprünglichen Vektoren steht:
\[ \vec{a} \times \vec{b} = \vec{c} \]
\[ \vec{c} = \vec{a} \times \vec{b} \]
\[ \rightarrow \quad \vec{c} \perp \vec{a}, \quad \vec{c} \perp \vec{b} \]
Das Vektorprodukt ist in drei Dimensionen definiert als:
\[ \begin{pmatrix} a_x \ a_y \ a_z \end{pmatrix} \times \begin{pmatrix} b_x \ b_y \ b_z \end{pmatrix} = \begin{pmatrix} a_y b_z – a_z b_y \ a_z b_x – a_x b_z \ a_x b_y – a_y b_x \end{pmatrix} \]
Das Vektorprodukt ist nicht kommutativ: Eine Umkehrung der Reihenfolge kehrt das Vorzeichen um (Wechsel vom Rechtssystem zum Linkssystem):
\[ \vec{a} \times \vec{b} \;\; = \;\; -(\vec{b} \times \vec{a}) \]
Der Betrag (Länge) des neuen Vektors aus dem Vektorprodukt entspricht der Fläche des Parallelogramms, das durch die beiden ursprünglichen Vektoren gebildet wird:
\[ |\vec{c}| = |\vec{a} \times \vec{b}| = A \]
Kollineare Vektoren bilden ein verschwindendes Parallelogram, so dass sie einfach mit dem Vektorprodukt nachgewiesen werden können:
\[ |\vec{a} \times \vec{b}| = 0 \quad \Leftrightarrow \quad \vec{a} \uparrow \uparrow \vec{b} \;\; \text{oder} \;\; \vec{a} \uparrow \downarrow \vec{b} \]
Der Betrag des Vektorprodukt (=Fläche des Parallelogramms) kann mit den Beträgen der ursprünglichen Vektoren und dem Sinus des Zwischenwinkels berechnet werden:
\[ |\vec{a} \times \vec{b}| \;\; = \;\; |\vec{a}| \cdot |\vec{b}| \cdot \sin(\varphi) \]
Häufigste Fragen
Vektorprodukt in der Komponentenschreibweise
Bei der Einführung des Skalarprodukts haben wir gelernt, dass das Produkt einen Skalar, d.h. eine Zahl produziert. Das Vektorprodukt heisst natürlich so, weil das Produkt einen Vektor produziert. Statt Vektorprodukt findet man auch die Ausdrücke Kreuzprodukt, Vektorprodukt oder äusseres Produkt. Wir schauen uns ein erstes Beispiel an, ohne zu wissen, wie das Vektorprodukt gerechnet wird:
\[ \vec{a} \times \vec{b} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 3 \\ 4 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 12 \end{pmatrix} = \vec{c} \]
Als Erstes sehen wir, dass statt einem Punkt hier ein Kreuz als Produktsymbol verwendet wird. Zweitens entsteht aus den beiden Vektoren \(\vec{a}\) und \(\vec{b}\) tatsächlich ein dritter Vektor \(\vec{c}\). Jetzt zur Frage, wie ein solches Vektorprodukt gerechnet wird. Es ist ein bisschen komplizierter als das Skalarprodukt. Jede Komponente des neuen Vektors \(\vec{c}\) wird einzeln aus den Komponenten der Vektoren \(\vec{a}\) und \(\vec{b}\) berechnet: Als Erstes empfiehlt es sich die \(x\)- und \(y\)-Komponenten der beiden Vektoren \(\vec{a}\) und \(\vec{b}\) nochmals unter die Vektoren zu schreiben. Wir sehen gleich warum.
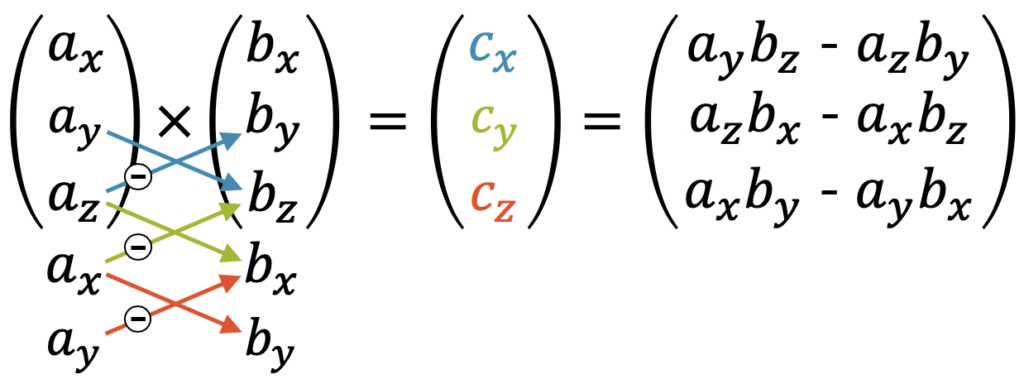
Jetzt gehen wir für die \(x\)-Komponente des Vektors \(\vec{c}\) eine Zeile nach unten und multiplizieren die \(y\)-Komponente von \(\vec{a}\) mit der \(z\)-Komponente von \(\vec{b}\). Dann subtrahieren wir das Produkt von \(a_z\) mit \(b_y\). Die beiden blauen Pfeile zeigen den Rechenvorgang. Wir erhalten den Ausdruck \((a_y b_z – a_z b_y)\) und schreiben das als \(x\)-Komponente von \(\vec{c}\) hin.
Jetzt rutschen wir eine Zeile nach unten und wiederholen diese Rechnung. Wir sehen jetzt, warum wir die \(x\)- und \(y\)-Komponenten unter die beiden Vektoren hingeschrieben haben. Wir schauen uns nochmals unser erstes Beispiel an und verstehen jetzt, wie das Vektorprodukt berechnet worden ist:
\[ \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 3 \\ 4 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \cdot 0 – 0 \cdot 4 \\ 0 \cdot 3 – 3 \cdot 0 \\ 3 \cdot 4 – 0 \cdot 3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 12 \end{pmatrix} \]
An dieser Stelle möchte ich auf etwas hinweisen, was beim Vektorprodukt eine wichtige Rolle spielt. Betrachte die Komponenten des Vektors \(\vec{a}\) von oben nach unten. Sie stehen in der Reihenfolge \(x, y, z\) und dann wieder \(x, y, (z)\). Schau Dir jetzt die Komponenten im berechneten Vektor an, auch wieder vertikal. Wir haben in der ersten “Spalte” \(a_y, a_z, a_x\). Das ist die gleiche Reihenfolge, nur mit dem Unterschied, dass wir mit \(y\), statt mit \(x\) angefangen haben. Die Reihenfolge ist aber die Gleiche. Die zweite “Spalte” ist \(b_z, b_x, b,y\). Auch hier wieder die gleiche Reihenfolge, jedoch mit \(z\) startend. Es sind sog. zyklische Permutationen der gleichen Reihenfolge, nämlich \(x, y, z\):
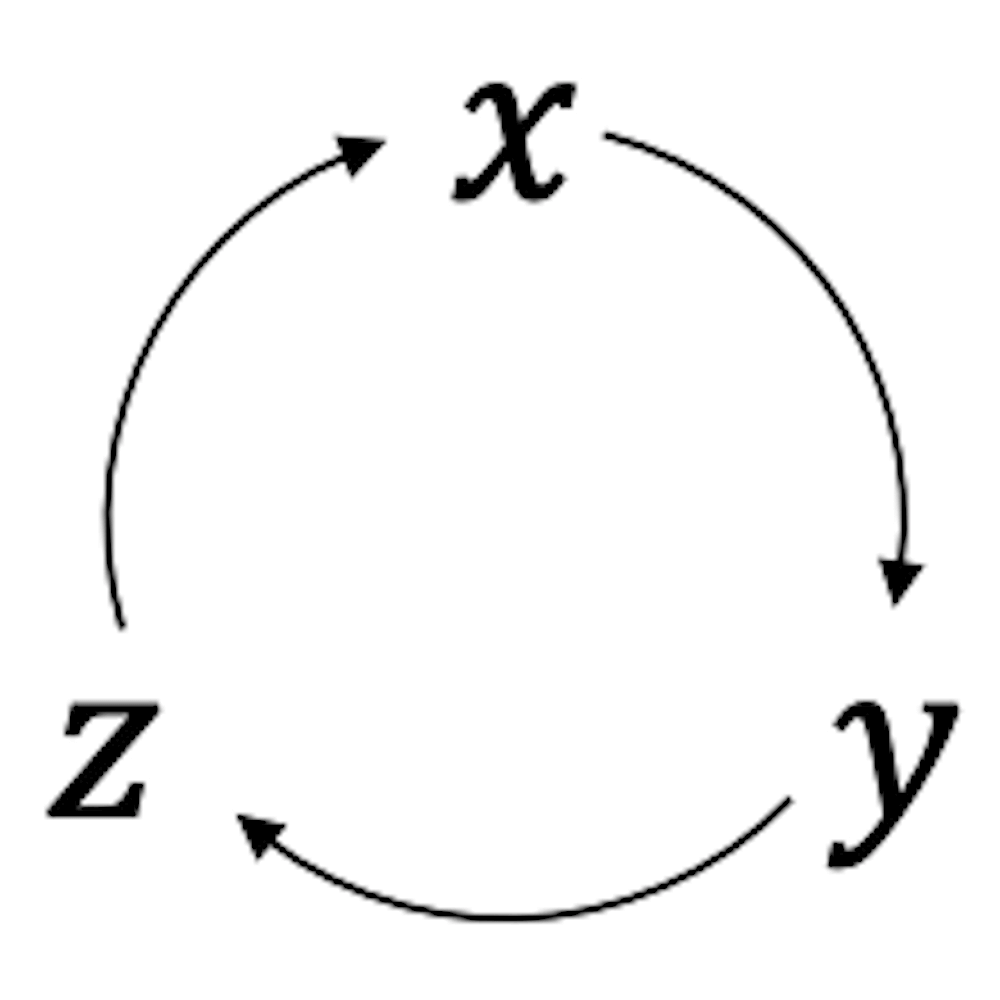
Vektorprodukt
\[ \vec{a} \times \vec{b} = \vec{c} \]
\[ \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} \times \begin{pmatrix} b_x \\ b_y \\ b_z \end{pmatrix} = \begin{pmatrix} a_y b_z – a_z b_y \\ a_z b_x – a_x b_z \\ a_x b_y – a_y b_x \end{pmatrix} \]
Beachte, dass wenn wir uns auf zwei Dimensionen beschränken, es kein Vektorprodukt gibt. Das Vektorprodukt braucht mindestens drei Dimensionen.
Algebraische Eigenschaften
Wir haben bei der Subtraktion und Addition gesehen, dass wir mit Vektoren rechnen können, auch ohne mit ihren Komponenten zu arbeiten. Das gilt auch beim Vektorprodukt, wo wir unser Algebra-Wissen einsetzen können. Allerdings gibt es einen grossen Unterschied zum normalen Zahlenprodukt, das wir aus der Algebra kennen: Das Vektorprodukt ist nicht kommutativ, d.h. wir können die Reihenfolge der Vektoren nicht einfach so umkehren. Was heisst das? Das normale Zahlenprodukt ist kommutativ. Ob wir 2 mit 3 multiplizieren oder 3 mit 2 ergibt das gleiche Resultat:
\[ 2 \cdot 3 \;\; = \;\; 3 \cdot 2 \qquad \leftrightarrow \qquad a \cdot b \;\; = \;\; b \cdot a \]
Auch das Skalarprodukt ist kommutativ. Die Reihenfolge spielt keine Rolle:
\[ \vec{a} \cdot \vec{b} \;\; = \;\; \vec{b} \cdot \vec{a} \]
Das Vektorprodukt ist nicht kommutativ: Die Reihenfolge, wie das Produkt gebildet wird, spielt eine Rolle auf das Vorzeichen: Bei einer Umkehrung der Reihenfolge kehrt auch das Vorzeichen um.
Das Vektorprodukt ist nicht kommutativ: Eine Umkehrung der Reihenfolge kehrt das Vorzeichen um:
\[ \vec{a} \times \vec{b} \;\; = \;\; -(\vec{b} \times \vec{a}) \]
Damit haben wir die spezielle algebraische Eigenschaft des Vektorprodukts abgehakt. Für die anderen algebraischen Eigenschaften können wir gleich verfahren, wie mit bisherigen Produkten. Wir müssen einfach mit der Reihenfolge aufpassen, denn es passiert sehr schnell, dass man die zwingende Einhaltung der Reihenfolge beim Vektorprodukt vergisst.
Beim nächsten Gesetz handelt es sich um das Distributivgesetz, das wir in der Algebra benutzen für das “Hineinmultiplizieren” in eine Klammer oder, wenn wir umgekehrt vorgehen, für das Ausklammern eines gemeinsamen Faktors.
Distributivgesetz für das Vektorprodukt:
\[ \vec{a} \times (\vec{b} + \vec{c}) \;\; = \;\; \vec{a} \times \vec{b} \;\; + \;\; \vec{a} \times \vec{c} \]
bzw.
\[ (\vec{a} + \vec{b}) \times \vec{c} \;\; = \;\; \vec{a} \times \vec{c} \;\; + \;\; \vec{b} \times \vec{c} \]
Das nächste Gesetz heisst Assoziativgesetz. Es geht darum, dass bei einem zweifachen Produkt von drei Zahlen es nicht darauf ankommt, ob zuerst ein Produkt mit den ersten beiden Zahlen gebildet wird oder erst die zweite und die dritte Zahl multipliziert werden:
\[ (2 \cdot 3) \cdot 4 = 2 \cdot (3 \cdot 4) \]
In der Kombination mit dem Vektorprodukt gilt das Assoziatativgesetz auch weiterhin.
Assoziativgesetz für die Kombination von Zahlenprodukt und Vektorprodukt. \(\vec{a}\) und \(\vec{b}\) sind Vektoren, \(\lambda\) ist ein Skalar, d.h. eine Zahl:
\[ \lambda \cdot (\vec{a} \times \vec{b}) \;\; = \;\; (\lambda \vec{a}) \times \vec{b} \]
\[ = \;\; \vec{a} \times (\lambda \vec{b}) \]
Die Reihenfolge im Vektorprodukt bleibt erhalten (\(\vec{a}\) vor \(\vec{b}\)), während die Reihenfolge für das Zahlenprodukt keine Rolle spielt (\(\lambda\) vor \(\vec{a}\) oder \(\vec{a}\) vor \(\lambda\)).
Beispiel: Distributivgesetz
Berechne den Ausdruck \((\vec{a} \times \vec{b}) + (\vec{a} \times \vec{c})\) mit
\[ \vec{a} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix}, \quad \vec{c} = \begin{pmatrix} 0 \\ 2 \\ -1 \end{pmatrix} \]
Lot auf der Ebene
Der neue Vektor steht senkrecht auf den beiden Vektoren, die das Vektorprodukt bilden. Das ist auch der Grund, warum des das Vektorprodukt nur in der räumlichen Vektorgeometrie gibt, denn zwei Vektoren in der \(x,y\)-Ebene erzeugen mit dem Vektorprodukt einen Vektor, der senkrecht auf ihnen steht, d.h. der parallel zur \(z\)-Achse ist – und schon haben wir die dritte Dimension.
Das Vektorprodukt steht senkrecht auf beiden ursprünglichen Vektoren, die im Produkt stehen:
\[ \vec{c} = \vec{a} \times \vec{b} \]
\[ \rightarrow \quad \vec{c} \perp \vec{a}, \quad \vec{c} \perp \vec{b} \]
Die beiden Vektoren \(\vec{a}\) und \(\vec{b}\) spannen zusammen eine Ebene auf, wie alle Vektorenpaare, sofern sie nicht kollinear sind. Der Vektor \(\vec{c}\), der durch das Vektorprodukt entsteht, steht senkrecht auf beiden Vektoren und somit senkrecht auf ihrer gemeinsamen Ebene.
Beispiel: Senkrechte Vektoren
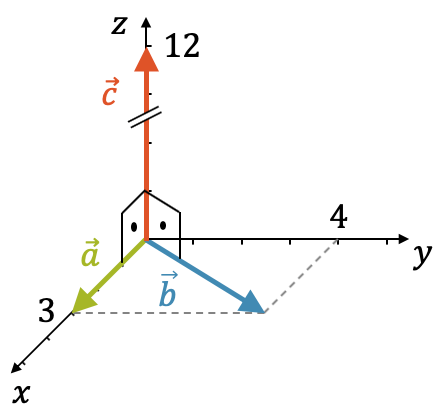
Überprüfe, dass \(\vec{c} = \vec{a} \times \vec{b}\) wirklich senkrecht auf \(\vec{a}\) und \(\vec{b}\) steht.
\[ \vec{a} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 3 \\ 4 \\ 0 \end{pmatrix} \]
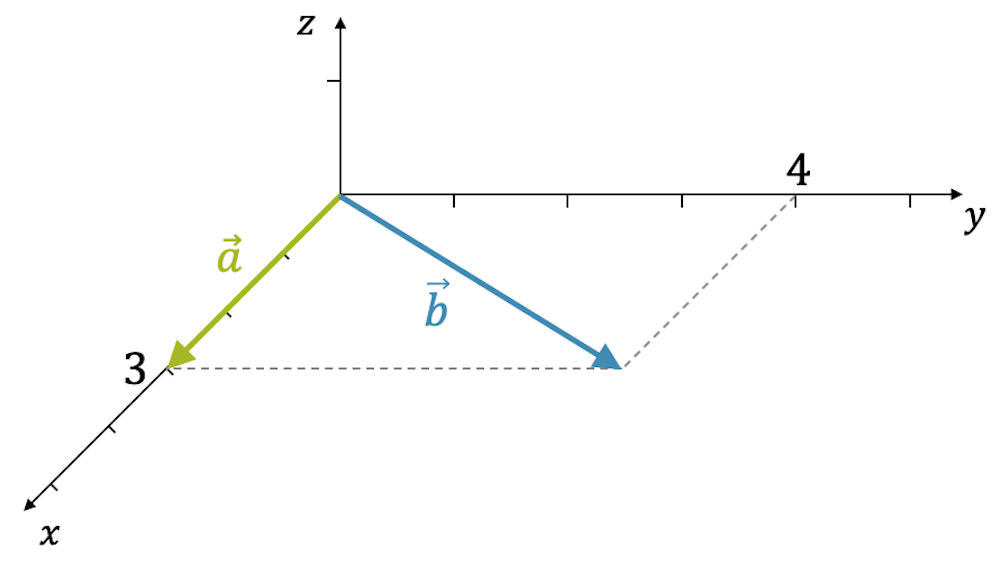
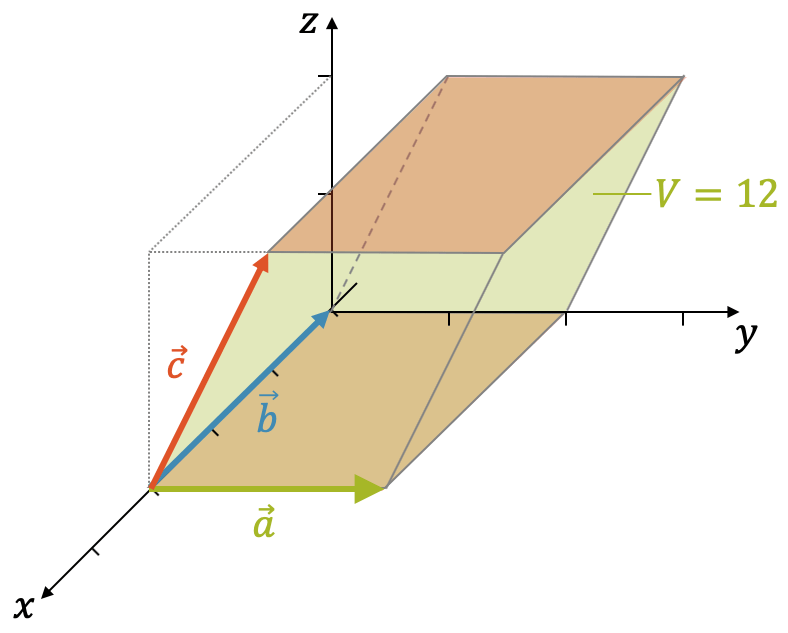
Fläche des Parallelogramms
Der Betrag (Länge) des neuen Vektors aus dem Vektorprodukt entspricht der Fläche des Parallelogramms, das durch die beiden ursprünglichen Vektoren gebildet wird:
\[ |\vec{c}| = |\vec{a} \times \vec{b}| = A \]
Wir überprüfen dies an unserem bekannten Beispiel:
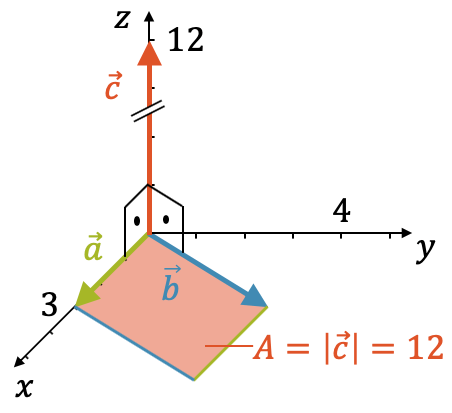
Von oben gesehen wird schnell klar, dass die Fläche tatsächlich \(12\) entspricht, denn wir haben ein Parallelogramm mit einer Grundseite von \(s=|\vec{a}|=3\) und einer Höhe \(h=4\). Wir erkennen auch zwei rechtwinklige Dreiecke, die zusammen ein Rechteck bilden mit der Fläche \(A=3 \cdot 4\).
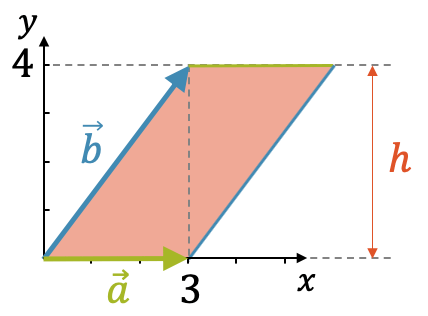
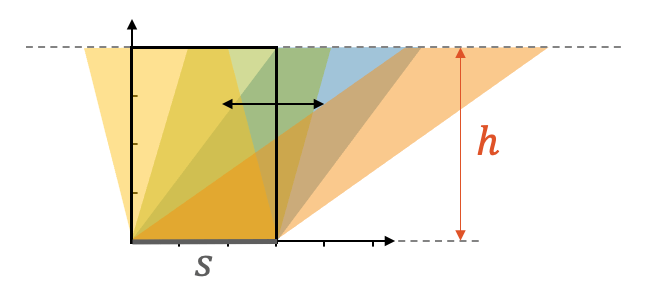
Beachte, dass sämtliche Parallelogramme, auch solche, die nicht genau zwei rechtwinklige Dreiecke ergeben, immer die gleiche Fläche \(A\) haben, nämlich Grundseite \(s\) mal Höhe \(h\), unabhängig davon, wie stark das Parallelogramm “verschoben” ist.
\[ A = s \cdot h \]
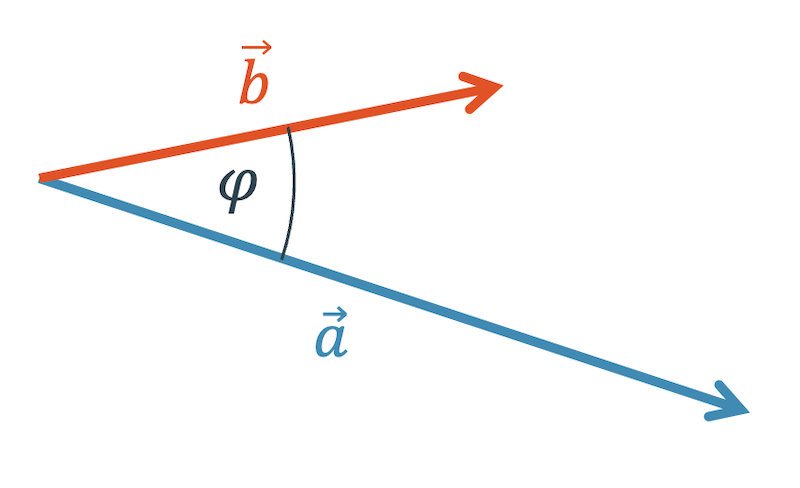
Der Betrag des Vektorprodukts kann auch anhand der Beträge der ursprünglichen Vektoren und ihrem Zwischenwinkel \(\varphi\) ermittelt werden:
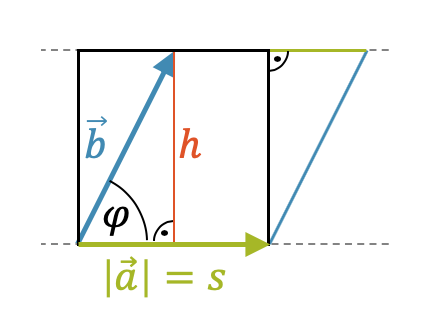
Im rechtwinkligen Dreieck gilt für das Verhältnis von Gegenkathete und Hypotenuse:
\[ \frac{h}{|\vec{b}|} = \sin(\varphi) \quad \rightarrow \quad h = |\vec{b}| \cdot \sin(\varphi) \]
Damit haben wir die Höhe \(h\) unseres Parallelogramms gefunden. Für die Fläche des Parallelogramms multiplizieren wir noch mit der \(s=|\vec{a}|\) und erhalten so einen neuen Ausdruck für den Betrag des Vektorprodukts:
\[ |\vec{a} \times \vec{b}| = A = s \cdot h \]
\[ = |\vec{a}| \cdot |\vec{b}| \cdot \sin(\varphi) \]
Der Betrag des Vektorprodukt (=Fläche des Parallelogramms) kann mit den Beträgen der ursprünglichen Vektoren und dem Sinus des Zwischenwinkels berechnet werden:
\[ |\vec{a} \times \vec{b}| \;\; = \;\; |\vec{a}| \cdot |\vec{b}| \cdot \sin(\varphi) \]
Wenn der Zwischenwinkel verschwindet oder 180\)^\circ\) ist, d.h. \(\vec{a}\) und \(\vec{b}\) kollinear sind, d.h. parallel verlaufen (gleich oder gegenläufig gerichtet), dann erhalten wir mit dem Vektorprodukt der beiden Vektoren den Nullvektor, da \(\sin(0^\circ)=\sin(180^\circ)=0\).
Kollineare Vektoren bilden im Vektorprodukt den Nullvektor:
\[ |\vec{a} \times \vec{b}| = 0 \quad \Leftrightarrow \quad \vec{a} \uparrow \uparrow \vec{b} \;\; \text{oder} \;\; \vec{a} \uparrow \downarrow \vec{b} \]
Wir wissen, dass der Sinus auch negative Werte annimmt. Wenn wir dies in die obige Formel einsetzen, müsste das Vektorprodukt manchmal auch “negative Flächen” liefern. Gibt es ein negatives Vektorprodukt?
Wir betrachten wieder unser bekanntes Beispiel mit \(\vec{a} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}\) und \(\vec{b} = \begin{pmatrix} 3 \\ 4 \\ 0 \end{pmatrix}\). Der Zwischenwinkel lässt sich mit Trigonometrie einfach bestimmen:
\[ \cos(\varphi) = \frac{|\vec{a}|}{|\vec{b}|} = \frac{3}{5} \quad \rightarrow \quad \varphi = 53.1^\circ \]
Wir nehmen jetzt einfach den gleichen Vektor \(\vec{a}\) und tragen mit dem gleichen Winkel \(\varphi\), dieses Mal aber im Uhrzeigersinn nach unten ab. Dort soll der Vektor \(\vec{d}\) sein. Wir wählen ihn so, dass er die gleiche Länge hat, wie \(\vec{a}\):
\[ |\vec{d}| = |\vec{a}| \]
Damit haben wir ganz sicher das gleiche Parallelogramm, einfach nur an der \(x\)-Achse gespiegelt. Die Fläche \(A\) sollte aber gleich gross sein.
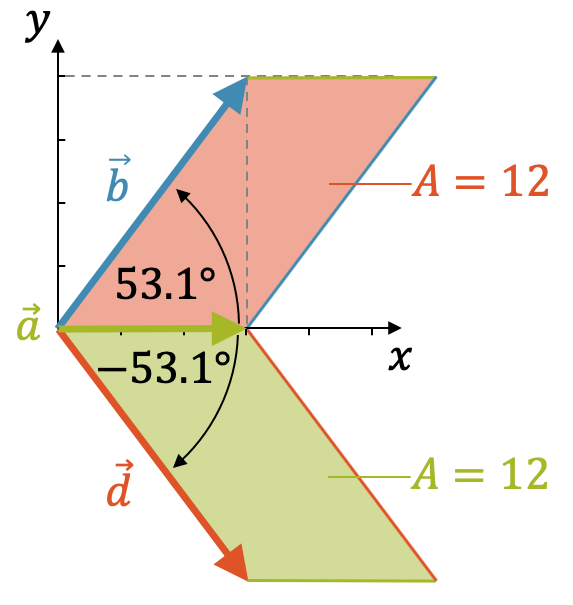
Wir erinnern uns an die trigonometrischen Funktionen im Einheitskreis. Dort hatten wir festgehalten, dass die \(x\)-Achse dem Winkel \(0°\) entspricht. Ab hier würde der Winkel \(\varphi\) im Gegenuhrzeigersinn zunehmen. Entsprechend steht der Uhrzeigersinn für das Abnehmen eines Winkels, d.h. von der \(x\)-Achse um 53.1\)^ \circ\) im Uhrzeigersinn gedreht, erhalten wir den Winkel von -53.1\)^ \circ\) für den Vektor \(\vec{d}\).
Für die Fläche der beiden Parallelogramme erhalten wir so:
\[ A_1 = |\vec{a} \times \vec{b}| = |\vec{a}| \cdot |\vec{b}| \cdot \sin(53.1^\circ) = 12 \]
\[ A_2 = |\vec{a} \times \vec{d}| = |\vec{a}| \cdot |\vec{d}| \cdot \sin(-53.1^\circ) = -12 \]
Die Flächen sind gleich gross, aber die untere Fläche hat ein negatives Vorzeichen. Achtung! Das hat nichts damit zu tun, dass sie unter der \(x\)-Achse steht! Der Grund für das negative Vorzeichen kommt vom Vorzeichen des Winkels und dieser ist negativ, weil wir vom ersten Vektor zum zweiten Vektor im Uhrzeigersinn gedreht haben.
Ein Winkel hat eigentlich keine Richtung. Der Zwischenwinkel ist in beiden Beispielen einfach \(\varphi = 53.1^\circ\). Es kommt beim Vektorprodukt aber auf die Reihenfolge der Vektoren an.
Rechtssystem
Als Rechtssystem verstehen wir in der Mathematik und Physik ein räumliches System mit einer bestimmten Reihenfolge. Das Vektorprodukt ist ein solches Rechtssystem, denn die Reihenfolge, mit welcher das Vektorprodukt gerechnet wird, bestimmt das Vorzeichen. Der Betrag des Vektorprodukts ist in beiden Fällen gleich, nämlich die Fläche des Parallelogramms. Ob das Vorzeichen der Fläche aber positiv oder negativ ist, bestimmt die Reihenfolge der beiden Vektoren und damit auch in welche Richtung der Zwischenwinkel \(\varphi\) vom ersten zum zweiten Vektor drehen musste.
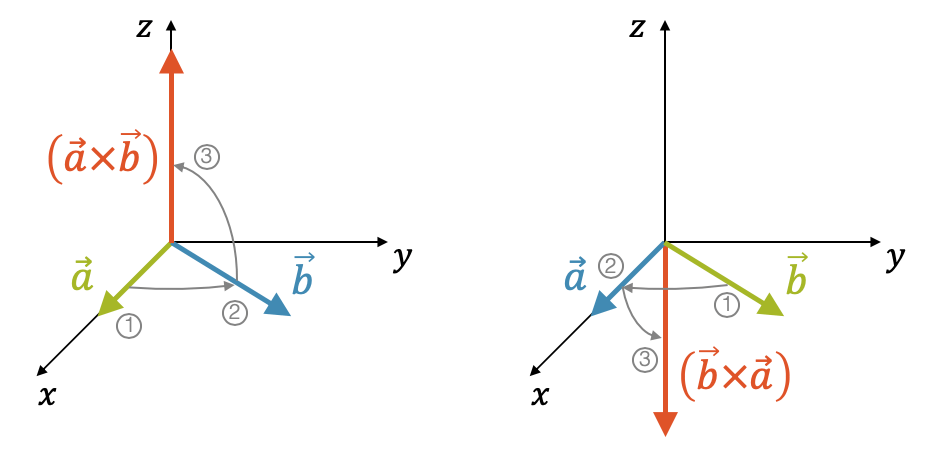
Im obigen Beispiel sehen wir links das Vektorprodukt \((\vec{a} \times \vec{b})\). Von oben gesehen drehen wir von \(\vec{a}\) nach \(\vec{b}\) im Gegenuhrzeigersinn und somit wird das Vektorprodukt positiv. Die Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) bilden ein Rechtssystem.
Wenn wir die Reihenfolge ändern (rechte Seite) und das Vektorprodukt \((\vec{b} \times \vec{a})\) berechnen, dann drehen wir von oben gesehen im Uhrzeigersinn und müssen deshalb ein negatives Vorzeichen setzen. Wir können den Vorgang auch von unten anschauen. Dann ist die Drehung im Gegenuhrzeigersinn und wir würden ein positives Vorzeichen erwarten. Allerdings heisst das, ein positives Vorzeichen nach unten, da wir ja von unten schauen. Ein positives Vorzeichen nach unten ist in Richtung der \((-z)\)-Achse, d.h. wir würden folgendes kriegen, was eigentlich wieder dem negativen Vorzeichen in \(z\)-Richtung entspricht:
\[ \vec{a} \times \vec{b} = 12 \cdot (-\vec{e}_z) = 12 \cdot \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} \]
\[ = \begin{pmatrix} 0 \\ 0 \\ -12 \end{pmatrix} \]
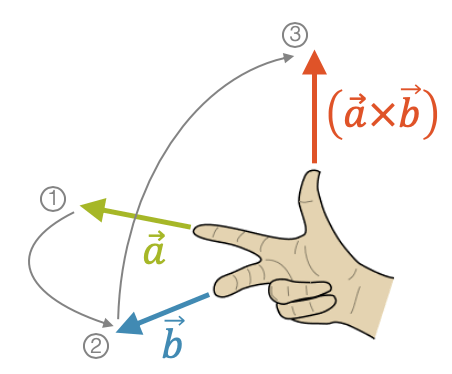
Rechtssysteme werden oft mit der Rechte–Hand–Regel erklärt. Die Schweizer Zweihunderternote zeigt eine rechte Hand mit den drei Fingern, die zusammen ein Rechtssystem bilden.
Aufgabensammlung
Lernziele
- Du kannst das Vektorprodukt in Komponenten berechnen.
- Du kannst mit dem Vektorprodukt auch algebraisch rechnen und das Distributiv- und das Assoziativgesetz anwenden. Du weisst, dass das Vektorprodukt nicht kommutativ ist, weil das Vorzeichen ändert.
- Du weisst, dass das Vektorprodukt einen neuen Vektor generiert, der auf den beiden ursprünglichen Vektoren senkrecht steht.
- Du weisst auch, dass der Betrag des Vektorprodukts der Fläche der eingeschlossenen Parallelogramms zwischen den beiden Vektoren entspricht. Ausserdem kann er mit dem Produkt der zwei Beträge der ursprünglichen Vektoren und dem Sinus ihres Zwischenwinkels berechnet werden.
- Das Vorzeichen des Vektorprodukts entspricht der Regel eines Rechtssystems, die von der Reihenfolge der Produktbildung abhängt. Du kannst dies z.B. mit Hilfe der rechten Hand oder mit einer Skizze in eigenen Worten erklären.
Weitere Links
Kreuzprodukt (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.