Das Wichtigste in Kürze
Das Skalarprodukt von zwei Vektoren, wird berechnet, indem die \(x\)-Komponenten der beiden Vektoren miteinander multipliziert und mit dem Produkt der \(y\)-Komponenten addiert werden. Das Ergebnis ist eine Zahl (Skalar).
\[ \vec{a} = \begin{pmatrix}a_x \\ a_y\end{pmatrix}, \quad \vec{b} = \begin{pmatrix}b_x \\ b_y\end{pmatrix} \]
\[ \rightarrow \quad \vec{a} \cdot \vec{b} \;\; = \;\; a_x \cdot b_x + a_y \cdot b_y \]
In drei Dimensionen:
\[ \vec{a} = \begin{pmatrix}a_x \\ a_y \\ a_z\end{pmatrix}, \quad \vec{b} = \begin{pmatrix}b_x \\ b_y \\ b_z\end{pmatrix} \]
\[ \rightarrow \quad \vec{a} \cdot \vec{b} \;\; = \;\; a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z \]
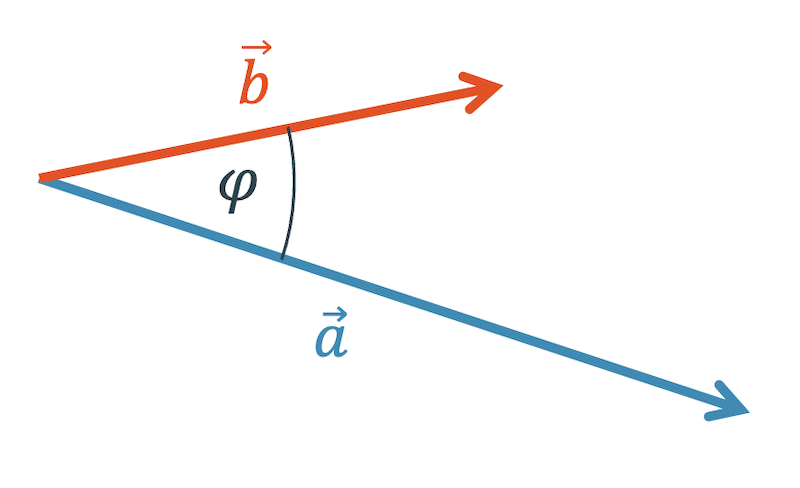
Mit dem Skalarprodukt Winkel \(\varphi\) berechnen: Das Skalarprodukt enthält das Produkt der beiden Vektorlängen \(|\vec{a}|\) und \(|\vec{b}|\) und den Kosinus des Zwischenwinkels \(\varphi\), der zwischen den beiden Vektoren eingeschlossen ist:
\[ \vec{a} \cdot \vec{b} \;\; = \;\; |\vec{a}| \cdot |\vec{b}| \cdot \cos(\varphi) \]
Aufgelöst nach dem Zwischenwinkel erhalten wir:
\[ \varphi = \arccos\Big(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\Big) \]
Da der Kosinus von 90° verschwindet (\(\cos(90^\circ) = 0\)), haben wir ein Skalarprodukt null wenn beide Vektoren senkrecht aufeinander stehen:
\[ \vec{a} \cdot \vec{b} = 0 \quad \Leftrightarrow \quad \vec{a} \perp \vec{b} \]
Video
-
Please login for access. Login -
Please login for access. Login
Häufigste Fragen
Du wirst hier verstehen, wie einfach mit dem Skalarprodukt Winkel berechnet werden können. Genauso einfach können wir bestimmen, ob zwei Vektoren senkrecht (orthogonal) zueinander sind. Das Skalarprodukt ist ein sehr praktisches Werkzeug. Wir werden seine Definition, typische Anwendungen und seine geometrische Bedeutung in der analytischen Geometrie (Vektorgeometrie) anschauen.
Warum heisst es ‘Skalarprodukt’?
Das Skalarprodukt ist ein Produkt von zwei Vektoren, d.h. zwei Vektoren werden durch eine mathematische Operation miteinander verknüpft, die einer Multiplikation ähnelt.
Durch diese Operation wird ein Zahlenwert berechnet, der in der Mathematik ‘Skalar’ bezeichnet wird (für mehr Informationen sei auf den Artikel in Wikipedia verwiesen). Für Skalare wird oft das Symbol \(\lambda\) verwendet.
Das Skalarprodukt wird manchmal auch Punktprodukt oder inneres Produkt genannt, um es vom Kreuzprodukt bzw. äusseren Produkt, dem Vektorprodukt zu unterscheiden. Wie der Name sagt, führt das Vektorprodukt aus zwei Vektoren eine Art Multiplikation durch, deren Resultat dieses Mal ein Vektor ist.
Wie wird das Skalarprodukt berechnet?
Wir schauen uns ein kleines Beispiel an. Die Erklärung, wie es tatsächlich berechnet wird, folgt gleich. Es soll das Skalarprodukt des Vektors \(\vec{a}\) und des Vektors \(\vec{b}\) berechnet werden:
\[ \vec{a} = \begin{pmatrix}1 \\ 4\end{pmatrix}, \quad \vec{b} = \begin{pmatrix}3 \\ 5\end{pmatrix} \]
Zuerst werden die beiden \(x\)-Komponenten der beiden Vektoren miteinander multipliziert:
\[ a_x = 1, \quad b_x = 3 \quad \rightarrow \quad a_x \cdot b_x = 1 \cdot 3 \]
Dann wird das Gleiche mit den beiden \(y\)-Komponenten gerechnet:
\[ a_y = 4, \quad b_y = 5 \quad \rightarrow \quad a_y \cdot b_y = 4 \cdot 5 \]
Schliesslich addieren wir die beiden Produkte:
\[ \vec{a} \cdot \vec{b} = 1 \cdot 3 + 4 \cdot 5 \]
\[ \rightarrow \quad \vec{a} \cdot \vec{b} = \underline{23} \]
Damit haben wir das Skalarprodukt von \(\vec{a}\) und \(\vec{b}\) berechnet.
Skalarprodukt Definition
In zwei Dimensionen gilt:
\[ \vec{a} = \begin{pmatrix}a_x \\ a_y\end{pmatrix}, \quad \vec{b} = \begin{pmatrix}b_x \\ b_y\end{pmatrix} \]
\[ \rightarrow \quad \vec{a} \cdot \vec{b} \;\; = \;\; a_x \cdot b_x + a_y \cdot b_y \]
Im dreidimensionalen Fall kommt noch die dritte Dimension hinzu, d.h. das Produkt der \(z\)-Komponenten. Das Skalarprodukt kann aber auch in vier Dimensionen bzw. in noch höheren Dimensionen auf die gleiche Art berechnet werden:
\[ \vec{a} = \begin{pmatrix}a_x \\ a_y \\ a_z\end{pmatrix}, \quad \vec{b} = \begin{pmatrix}b_x \\ b_y \\ b_z\end{pmatrix} \]
\[ \rightarrow \quad \vec{a} \cdot \vec{b} \;\; = \;\; a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z \]
Verallgemeinert auf \(n\) Dimensionen erhalten wir:
\[ \vec{a} \cdot \vec{b} \;\; = \;\; \sum_{k=1}^n \big(a_k \cdot b_k\big) \]
Die Variable \(k\) läuft im Summenzeichen von 1 bis \(n\). Von der \(k\)-ten Komponente des Vektors \(\vec{a}\) bzw. \(\vec{b}\), d.h. \(a_k\) und \(b_k\) wird das Produkt \(a_k b_k\). All diese Produkte werden schliesslich summiert.
Zusammenhang zwischen Vektorlängen und Zwischenwinkel
Für das Skalarprodukt existiert auch eine andere Formel, die etwas komplizierter ist:
\[ \vec{a} \cdot \vec{b} \;\; = \;\; |\vec{a}| \cdot |\vec{b}| \cdot \cos(\varphi) \]
Es ist das Produkt von drei Grössen:
- Länge (Norm) des Vektors: \(|\vec{a}|\)
- Länge (Norm) des Vektors: \(|\vec{b}|\)
- Kosinuswert des Zwischenwinkels \(\varphi\): \(\cos\big(\varphi\big)\)
Für die Länge nennt sich auch Norm des Vektors \(\vec{a}\) wird die Wurzel der Summe der Quadrate der Vektorkomponenten genommen:
\[ |\vec{a}| = \sqrt{a_x^2 + a_y^2} \]
In drei Dimensionen gilt:
\[ |\vec{a}| = \sqrt{a_x^2 + a_y^2 + a_z^2} \]
Die Längen des Vektors \(\vec{b}\) wird analog berechnet.
Der Zwischenwinkel \(\varphi\) ist der Winkel zwischen den beiden Vektoren. Dabei kommt es nicht darauf an, ob der Winkel spitz oder stumpf ist, denn die Kosinus-Funktion liefert in beiden Fällen den gleichen Wert.
Beispiel: Skalarprodukt zweier Vektoren mit gleicher Richtung
Bilde das Skalarprodukt der beiden Vektoren \(\vec{u}\) und \(\vec{v}\), die die gleiche Richtung haben, aber eine unterschiedliche Länge:
\[ \vec{u} = \begin{pmatrix}1.2 \\ 1.6\end{pmatrix}, \quad \vec{v} = \begin{pmatrix}3 \\ 4\end{pmatrix} \]
Vergleiche das Resultat mit den beiden Längen.
Beispiel: Mit dem Skalarprodukt Winkel von 60° nachweisen
Zeige mit Hilfe des Skalarprodukts, dass die Punkte \(A\), \(B\) und \(C\) ein gleichseitiges Dreieck bilden mit drei Winkeln à 60°.
\[ A\Big(-\frac{1}{2}, 0\Big), \quad B\Big(0,\frac{\sqrt{3}}{2}\Big), \quad C\Big(\frac{1}{2}, 0\Big) \]
Die wichtigsten Spezialfälle der Kosinus-Funktion
Der Kosinus ist eine trigonometrische Funktion für welche wir meistens den Taschenrechner brauchen. Es gibt aber die folgenden drei Spezialfälle, die wir auswendig kennen sollten:
- Gleich gerichtete Vektoren: Zwischenwinkel \(\varphi = 0^\circ\)
- Senkrechte Vektoren: Zwischenwinkel \(\varphi = 90^\circ\)
- Genau entgegen gesetzte Vektoren Zwischenwinkel \(\varphi = 180^\circ\)
Für diese drei Fälle sind die Werte der Kosinus-Funktion sehr einfach:
- \(\varphi = 0^\circ \quad \rightarrow \quad \cos(0^\circ) = 1\)
- \(\varphi = 90^\circ \quad \rightarrow \quad \cos(90^\circ) = 0\)
- \(\varphi = 180^\circ \quad \rightarrow \quad \cos(180^\circ) = -1\)
In den beiden Fällen, wo der Kosinus 1 bzw. -1 beträgt, entspricht das Skalarprodukt dem Produkt der beiden Längen (abgesehen vom Vorzeichen). Wenn beide Vektoren senkrecht aufeinander stehen, ist das Skalarprodukt auf jeden Fall null.
Geometrische Bedeutung des Skalarprodukts
Um die geometrische Bedeutung ein bisschen einzukreisen, schauen wir uns einen allgemeinen Fall an, in welchem zwei Vektoren \(\vec{u}\) und \(\vec{v}\) den Zwischenwinkel \(\varphi\) einschliessen. Mit der zweiten Formel für das Skalarprodukt erhalten wir:
\[ \vec{u} \cdot \vec{v} = |\vec{u}| \cdot |\vec{v}| \cdot \cos(\varphi) \]
Wir dividieren durch die beiden Vektorlängen und erhalten so einen Ausdruck für den Kosinus von \(\varphi\). Für die beiden Vektorlängen benutzen wir die kurze Schreibweise \(u=|\vec{u}|\) bzw. \(v=|\vec{v}|\).
\[ \cos(\phi) = \frac{\vec{u} \cdot \vec{v}}{u \cdot v} \]
Wir können den Bruch auch anders schreiben, nämlich als Produkt von zwei Brüchen:
\[ \cos(\phi) = \frac{\vec{u}}{u} \cdot \frac{\vec{v}}{v} \]
Die beiden Brüche sind die Einheitsvektoren der ursprünglichen Vektoren \(\vec{u}\) und \(\vec{v}\). Einheitsvektoren entstehen, wenn ein Vektor durch seine eigene Länge geteilt wird:
\[ \vec{e}_u = \frac{\vec{u}}{u}, \quad \vec{e}_v = \frac{\vec{v}}{v} \]
Wir schreiben den Ausdruck für den Kosinus damit um:
\[ \cos(\varphi) = \vec{e}_u \cdot \vec{e}_v \]
Schau dir das nachfolgende Bild an. Wir nehmen hier den Endpunkt des Vektors \(\vec{e}_u\) und projizieren ihn auf \(\vec{v}\).
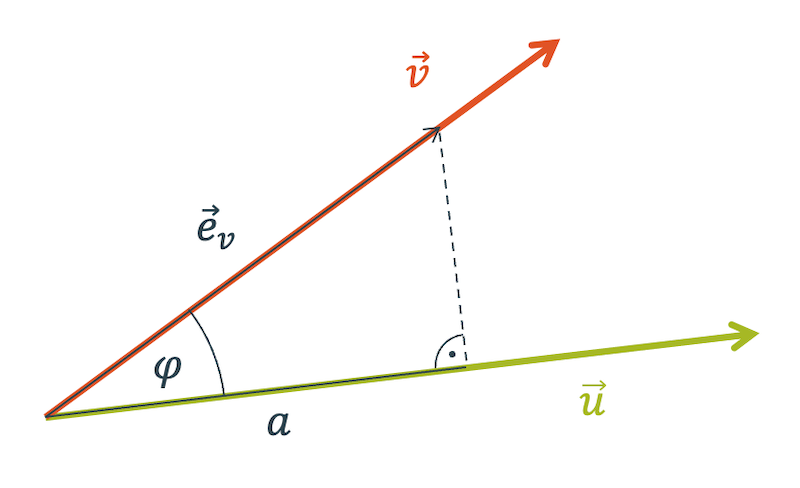
Dabei entsteht ein kleines rechtwinkliges Dreieck, dessen Hypotenuse die Länge 1 hat. Die Länge der Projektion auf dem Vektor \(\vec{u}\) ist die Ankathete, deren Länge in diesem Fall dem Kosinus von \(\varphi\) entspricht.
Das Skalarprodukt ist demnach das Produkt der Vektorlängen unter Berücksichtigung der Projektion des einen auf den anderen. Die Reihenfolge ist egal, weil das Skalarprodukt kommutativ ist, d.h. wir können die Reihenfolge vertauschen:
\[ \vec{u} \cdot \vec{v} \;\; = \;\; \vec{v} \cdot \vec{u} \]
So finden wir senkrechte Vektoren
Wir wissen jetzt, dass senkrechte Vektoren einen Zwischenwinkel \(\varphi=90^\circ\) haben und dass die Kosinusfunktion für 90° den Wert des Skalarprodukts auf null setzt:
\[ \cos(90^\circ) = 0 \]
\[ \rightarrow \quad \vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos(90^\circ) = 0 \]
Deshalb können wir mit dem Skalarprodukt sehr einfach überprüfen, ob zwei Vektoren senkrecht aufeinander stehen. Das funktioniert übrigens auch in drei Dimensionen für räumliche Vektoren!
Wenn mindestens einer der beiden Vektoren ein Nullvektor ist, d.h. ein Vektor mit lauter Nullen als Komponenten, dann wir das Skalarprodukt auch null sein. Wir können in diesem Fall aber nicht wirklich behaupten, dass die Vektoren senkrecht aufeinander stehen, denn ein Nullvektor hat keine Richtung.
In allen anderen Fällen gilt aber zuverlässig:
\[ \vec{a} \cdot \vec{b} = 0 \quad \Leftrightarrow \quad \vec{a} \perp \vec{b} \]
Beachte, dass das Skalarprodukt null ist, obwohl beide Vektoren selber nicht null sind! Vektoren verhalten sich offenbar anders als Zahlen. In einem Zahlenprodukt können wir nur null erhalten, wenn mindestens einer der beiden Faktoren null ist. Anders kann ein Zahlenprodukt unmöglich null sein. Bei den Vektoren geht das aber!
Beispiel: Skalarprodukt von zwei senkrechten Vektoren
Berechne das Skalarprodukt der beiden senkrecht aufeinander stehenden Vektoren \(\vec{a}\) und \(\vec{b}\).
\[ \vec{a} = \begin{pmatrix}1 \\ 1\end{pmatrix}, \quad \vec{b} = \begin{pmatrix}-2 \\ 2\end{pmatrix} \]
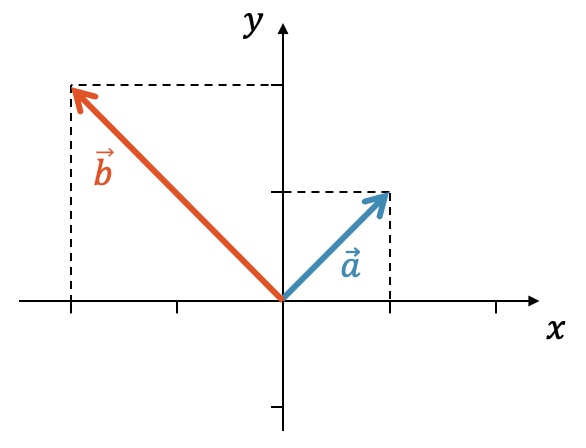
Beispiel: Senkrechten Vektor finden in drei Dimensionen
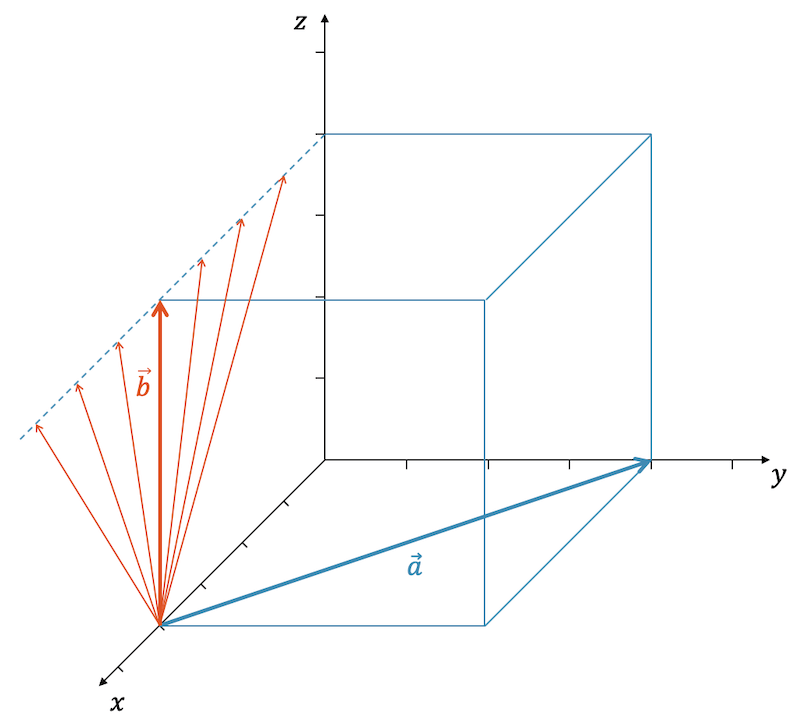
Wähle die Komponente \(b_x\) so, dass \(\vec{b}\) senkrecht auf \(\vec{a}\) steht. Zeichne beide Vektoren.
\[ \vec{a} = \begin{pmatrix}-4 \\ 4 \\ 0 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix}b_x \\ 0 \\ 4 \end{pmatrix} \]
“Der Zwischenwinkel kann auch mit dem Vektorprodukt berechnet werden.
Mit dem Skalarprodukt geht es aber meistens einfacher!”
Mit dem Skalarprodukt Winkel berechnen
Wir können beliebige Winkel zwischen zwei Vektoren bestimmen. Wir nehmen die zweite Formel für das Skalarprodukt:
\[ \vec{a} \cdot \vec{b} \;\; = \;\; |\vec{a}| \cdot |\vec{b}| \cdot \cos(\varphi) \]
Nun lösen wir nach dem Zwischenwinkel \(\varphi\) auf, indem wir die Gleichung durch die beiden Vektorlängen teilen:
\[ \cos(\varphi) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|} \]
Wir ersetzen die rechte Seite mit einer einfachen Variablen \(R\). Bei zwei gegebenen Vektoren, könnten wir sie berechnen. Wir bräuchten dazu das Skalarprodukt mit der ersten einfachen Formel und die beiden Vektorlängen. Wir nehmen deshalb an, dass \(R\) berechnet worden ist.
\[ \cos(\varphi) = R \]
Jetzt such wir den Winkel \(\varphi\), der im Kosinus \(R\) entspricht. Das erhalten wir mit der Umkehrfunktion des Kosinus: Der Arkuskosinus, der auf dem Taschenrechner meist mit \(\cos^{-1}\) angeschrieben ist.
\[ \cos(\varphi) = R \quad \rightarrow \quad \varphi = \arccos(R) \]
Damit haben wir die Formel, um mit Skalarprodukt den Winkel zwischen zwei Vektoren zu berechnen:
\[ \varphi = \arccos\Big(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\Big) \]
Das Vektorprodukt hat eine ähnliche Formel. Sie ist aber meistens aufwändiger und fehleranfälliger als diese Formel mit dem Skalarprodukt.
Beispiel: Berechnung des Zwischenwinkels von zwei Vektoren
Berechne den Zwischenwinkel zwischen den beiden Vektoren \(\vec{u}\) und \(\vec{v}\).
\[ \vec{u} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}, \quad \vec{v} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \]
Aufgabensammlung
Lernziele
- Du kannst das Skalarprodukt von zwei Vektoren im zwei- und dreidimensionalen Fall berechnen.
- Du weisst, dass das Skalarprodukt eines Vektors mit sich selbst dem Quadrat seiner Länge entspricht. Ebenso weisst du, dass das Skalarprodukt für zwei gleichgerichtete Vektoren dem Produkt der beiden Längen entspricht.
- Du weisst, dass das Skalarprodukt zweier senkrecht aufeinander stehender Vektoren verschwindet.
- Du kannst mit Hilfe des Skalarprodukts den Winkel zwischen zwei Vektoren bestimmen.
Mini-Test
Prüfe dein Wissen mit Hilfe eines kleinen Tests mit Verständnisfragen und Rechenaufgaben.
Um auf den Mini-Test zugreifen zu können,
musst du Mitglied im Hacker-Club sein.
Skalarprodukt (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.