Vektoren

Vektoren als Abbildungen von Punkten

Wir schauen uns als Erstes ein Beispiel an. In der nachfolgenden Grafik haben wir einen Pfeil der vom Punkt \(A\) zum Punkt \(A’\) zeigt. Genauso zeigt ein Pfeil vom Punkt \(B\) zu \(B’\) und von \(C\) zu \(C’\). Es fällt vielleicht auf, dass die Pfeile alle parallel zu einander und gleich lang sind. Es handelt sich tatsächlich um ein und denselben Vektor, den wir \(\;\vec{v}\;\) nennen.

Vektoren werden als solche gekennzeichnet, indem sie oben mit einem kleinen Pfeil versehen werden. In der Literatur gibt es auch die Schreibweisen in fett und mit einem Zirkumflex: \(\;\mathbf{v}\;\) oder \(\;\hat{v}\;\)

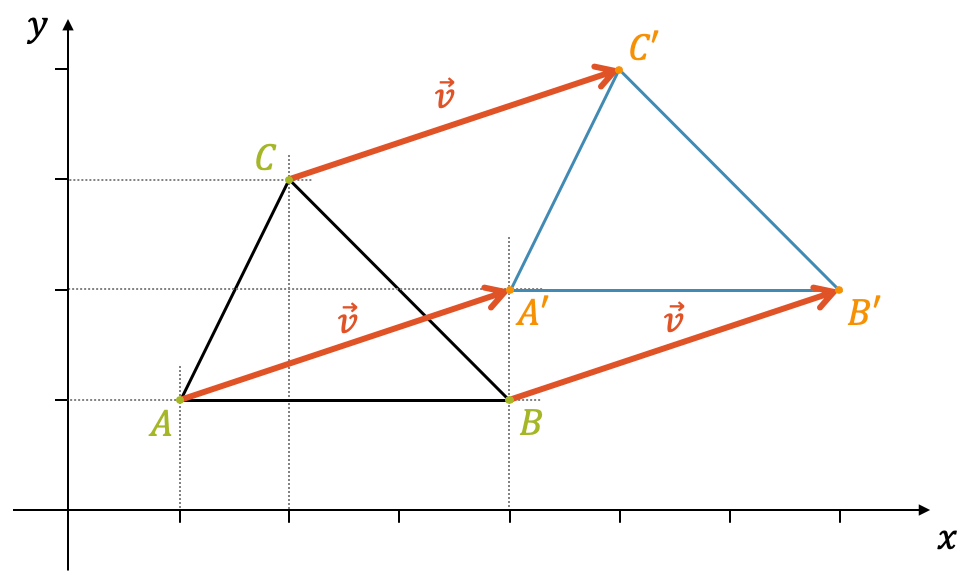
Der Vektor \(\overrightarrow{AA’}\) bildet den Punkt \(A\) in den Punkt \(A’\) ab:

\[ \overrightarrow{AA’}: \quad A(1,1) \; \mapsto \; A'(4,2) \]

Wenn wir die Abbildungen von \(B\) auf \(B’\) bzw. \(C\) auf \(C’\) anschauen, finden wir:

\[ \overrightarrow{BB’}: \quad B(4,1) \; \mapsto \; B'(7,2) \]

\[ \overrightarrow{CC’}: \quad C(2,3) \; \mapsto \; C'(5,4) \]

Wir sehen jetzt, dass \(\;\vec{v}\;\) in allen Fällen die gleiche Abbildung darstellt: Die \(x\)-Koordinate erhöht sich um  mit \(\Delta x = +3\) und die \(y\)-Koordinate erhöht sich um \(\Delta y = +1\). Es handelt sich in den drei Fällen um den gleichen Vektor \(\;\vec{v}\;\). Wir schreiben ihn mit seinen Komponenten mit einer Klammer. Oben steht die Änderung der \(x\)-Koordinate, unten die Änderung der \(y\)-Koordinate:

\[ \vec{v} = \begin{pmatrix} 3 \\ 1 \end{pmatrix} \]

Ein Vektor ist eine Abbildung von einem Punkt \(A(A_x,A_y)\) zu einem Punkt \(A'(A’_x,A’_y)\) mit einer Richtung und einer Länge:

\[ \vec{v}: \quad A(A_x,A_y) \; \mapsto \; A'(A’_x,A’_y) \]

Die Komponenten \(v_x\) und \(v_y\) des Vektors \(\vec{v}\) ergeben sich aus den Differenzen der Koordinaten der beiden Punkte. Wir können den Vektor auch als Verschiebung anschauen mit der Änderung der \(x\)-Koordinate um den Betrag \(v_x\) und der \(y\)-Koordinate um den Betrag \(v_y\):

\[ \vec{v} = \begin{pmatrix} v_x \\ v_y \end{pmatrix} = \begin{pmatrix} A’_x – A_x \\ A’_y – A_y \end{pmatrix} \]

Norm eines Vektors

Wie viel beträgt die Länge des Vektors, der den Punkt \(A(1,2)\) auf den Punkt \(B(6,1)\) abbildet?

Zuerst berechnen wir die Komponenten des Vektors \(\vec{v}\):

\[ \vec{v} = \begin{pmatrix} B_x – A_x \\ B_y – A_y \end{pmatrix} \]

\[ = \begin{pmatrix} 6 – 1 \\ 1 – 2 \end{pmatrix} = \begin{pmatrix} 5 \\ -1 \end{pmatrix} \]

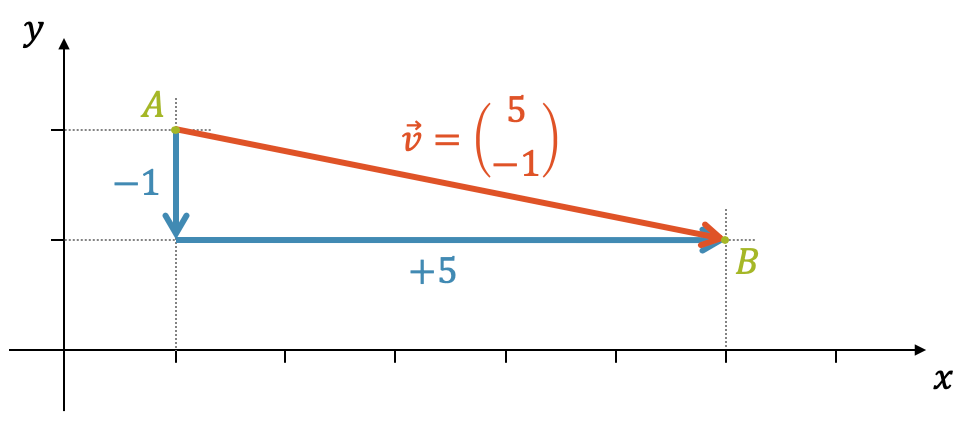
Für die Länge des Vektors benutzen wir natürlich den Satz des Pythagoras. Im Koordinatensystem haben wir mit der Horizontalen und der Vertikalen immer gleich ein rechtwinkliges Dreieck zur Hand. Die Länge des Vektors ist die Länge der Hypotenuse:

\[ |\vec{v}| = \sqrt{5^2 + (-1)^2} \]

\[ = \sqrt{25+1} = \sqrt{26} \approx 5.10 \]

Unter der Norm eines Vektors verstehen wir die Länge des Vektorpfeils. Sie wird aus den Komponenten \(v_x\) und \(v_y\) mit dem Satz des Pythagoras berechnet:

\[ \vec{v} = \begin{pmatrix} v_x \\ v_y \end{pmatrix} \quad \rightarrow \quad v = |\vec{v}| = \sqrt{v_x^2 + v_y^2} \]

Die Norm wird mit Betragsstrichen links und rechts des Vektors geschrieben. Meistens wird mit \(\,v\,\) (ohne Pfeil) automatisch auch die Norm von \(\,\vec{v}\,\) gemeint.

Einheitsvektor

Nebst der Länge eines Vektors, gibt es auch seine Richtung. Sie ist durch die beiden Komponenten des Vektors gegeben. Diese beinhalten aber auch die Länge des Vektors. Um die Richtung von der Länge zu trennen, können wir den Vektor einfach so verkürzen oder verlängern, dass seine Länge genau eins entspricht. Wenn ein Vektor die Länge eins hat, so heisst er Einheitsvektor.

Um einen Vektor mit der Länge eins zu erhalten, ohne seine Richtung zu verändern, teilen wir den Vektor durch seine eigene Länge bzw. wir multiplizieren ihn mit dem Kehrwert seiner Länge.

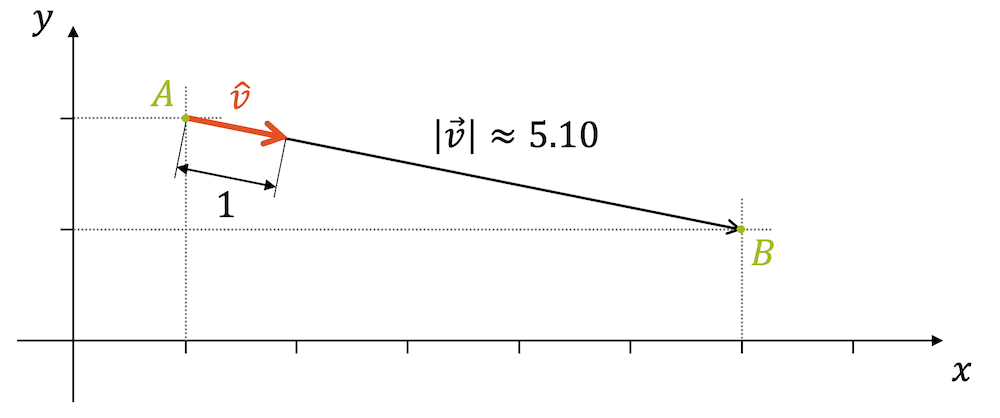
Der Einheitsvektor \(\vec{n}\) hat die gleiche Richtung wie \(\vec{v}\), aber er hat die Länge eins. Wir erhalten den Einheitsvektor, indem wir den Vektor \(\vec{v}\) durch seine eigene Länge teilen:

\[ \vec{n} = \frac{\;\vec{v}\;}{|\vec{v}|} \]

Gegenvektor

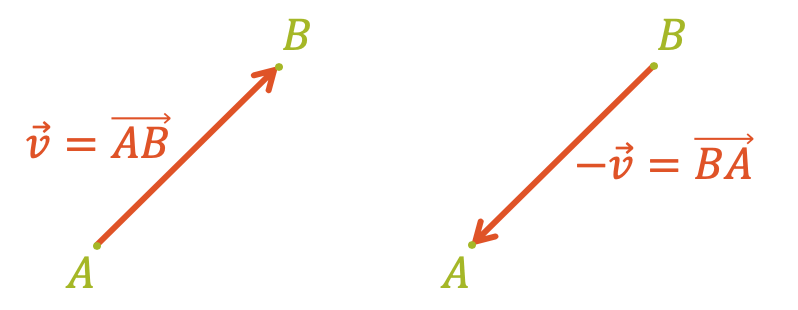
Als Gegenvektor bezeichnen wir einen gleich langen Vektor, der parallel zum ersten Vektor ist, aber entgegengesetzt in der Richtung. Er wird gebildet, indem der erste Vektor mit dem Faktor \((-1)\) multipliziert wird:

\[ \vec{v} = \overrightarrow{AB} \]

\[ \rightarrow \quad \overrightarrow{BA} = (-1) \cdot \vec{v} = -\vec{v} \]

Ortsvektor

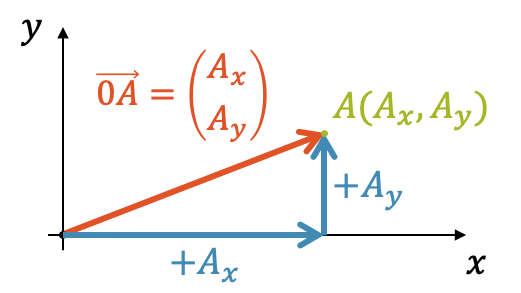
Unter dem Ortsvektor des Punktes \(A(A_x,A_y)\) verstehen wir einen Vektor, der vom Koordinatenursprung \(0\) zu diesem Punkt \(A\) zeigt.

\[ \overrightarrow{0A} = \begin{pmatrix} A_x \\ A_y \end{pmatrix} \]