Wenn wir z.B. den Vektor \(\vec{b}\) vom Vektor \(\vec{a}\) subtrahieren müssen, benutzen wir den Gegenvektor von \(\vec{b}\). So können wir jederzeit aus einer Subtraktion wieder eine Addition von zwei Vektoren machen, die wir ja kennen.
Für die Subtraktion von zwei Vektoren \(\vec{a}-\vec{b}\) brauchen wir den Gegenvektor von \(\vec{b}\): \((-\vec{b})\)
Wir addieren \(\vec{a}\) mit dem Gegenvektor von \(\vec{b}\):
\[ \vec{a} – \vec{b} \quad = \quad \vec{a} + (-\vec{b}) \]
Beispiel
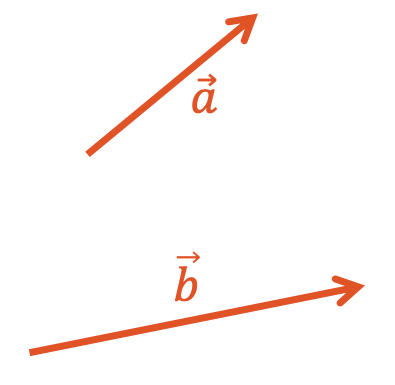
Subtrahieren Sie den Vektor \(\vec{b}\) vom \(\vec{a}\) mit der grafischen Methode.
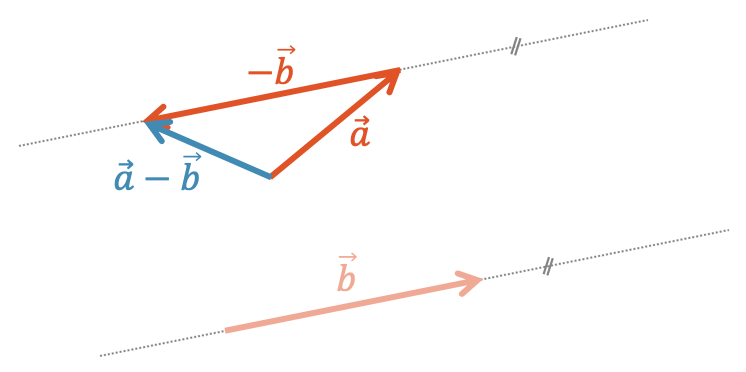
Wir ziehen wieder die Parallele von \(\vec{b}\) durch den Endpunkt von \(\vec{a}\) und zeichnen nun den Gegenvektor zu \(\vec{b}\). So kriegen wir die grafische Summe \(\vec{a} + (-\vec{b}) = \vec{a} – \vec{b}\).
Beispiel
Berechne die Differenz \((\vec{a}-\vec{b})\) und stelle sie grafisch dar.
\[ \vec{a} = \begin{pmatrix} 2 \\ 0 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 0 \\ -1 \end{pmatrix} \]
Wir schreiben die Differenz als Summe von \(\vec{a}\) und Gegenvektor \(-\vec{b}\) und addieren die Vektorkomponenten:
\[ (\vec{a} – \vec{b}) = \vec{a} + (-\vec{b}) \]
\[ = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ -(-1) \end{pmatrix} = \underline{\begin{pmatrix} 2 \\ 1 \end{pmatrix}} \]
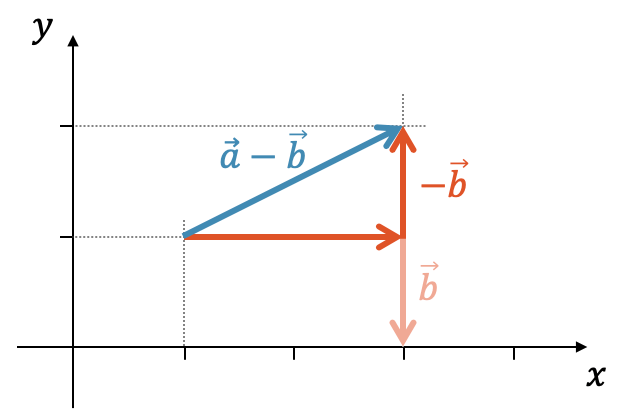
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.