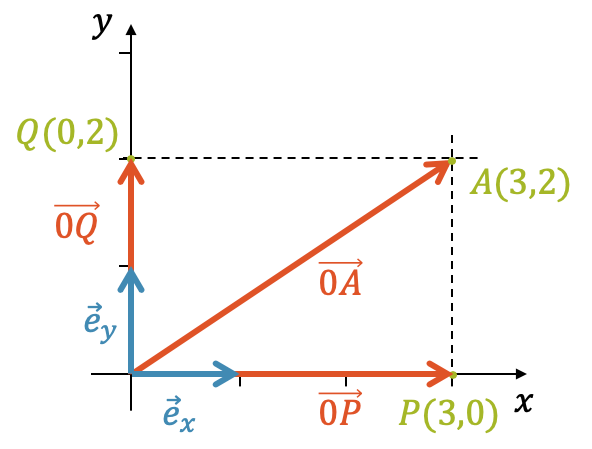
Wir betrachten zuerst den Punkt \(P(0,3)\). Er liegt auf der \(x\)-Achse. Wie kommen wir vom Ursprung zu diesem Punkt mit dem Einheitsvektor \(\vec{e}_x\)?
\[ k \cdot \vec{e}_x = \overrightarrow{0P} \quad \rightarrow \quad k \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 3 \\ 0 \end{pmatrix} \]
\[ \rightarrow \quad k=3 \]
Wir benutzen den dreifachen Einheitsvektor und sind dann am Ziel. Jetzt wiederholen wir das Prozedere und überlegen uns, wie wir mit dem Einheitsvektor \(\vec{e}_y\) vom Ursprung zum Punkt \(Q(2,0)\) gelangen.
\[ l \cdot \vec{e}_y = \overrightarrow{0Q} \quad \rightarrow \quad l \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \end{pmatrix} \]
\[ \rightarrow \quad l=2 \]
Hier brauchen wir einfach den doppelten Einheitsvektor. Wie kommen wir vom Ursprung zum Punkt \(A(3,2)\)? Mit dem Einheitsvektor \(\vec{e}_x\) alleine, können wir uns nur auf der \(x\)-Achse bewegen. Genauso wäre es nicht möglich, nur mit dem Einheitsvektor \(\vec{e}_y\) den Punkt \(A\) zu erreichen. Wir müssen die beiden Einheitsvektoren kombinieren.
\[ \overrightarrow{0A} \;\; = \;\; k \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + l \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} \]
\[ = \;\; \begin{pmatrix} 3 \\ 2 \end{pmatrix} \]
Wir kriegen:
\[ 3 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} \;\; = \;\; \begin{pmatrix} 3 \\ 2 \end{pmatrix} \]
Wir erreichen den Punkt \(A\) mit einer Linearkombination der beiden Einheitsvektoren \(\vec{e}_x\) und \(\vec{e}_y\):
\[ \overrightarrow{0A} = 3 \cdot \vec{e}_x + 2 \cdot \vec{e}_y \]
Es dürfte klar sein, dass wir beispielsweise den Punkt \(B(7,12)\) mit \(\overrightarrow{0B} = 7 \cdot \vec{e}_x + 12 \cdot \vec{e}_y\) erreichen können. Wir können sogar jeden Punkt in der \(x,y\)-Ebene mit Hilfe einer Linearkombination von \(\vec{e}_x\) und \(\vec{e}_y\) erreichen.
Aus diesem Grund sagt man auch, dass die beiden Vektoren \(\vec{e}_x\) und \(\vec{e}_y\) die \(x,y\)-Ebene aufspannen.
Mit Linearkombinationen der zwei Einheitsvektoren \(\vec{e}_x\) und \(\vec{e}_y\) erreichen wir alle Punkte der \(x,y\)-Ebene:
\[ P(x,y) \quad \rightarrow \quad \overrightarrow{0P} \;\; = \;\; x \cdot \vec{e}_x + y \cdot \vec{e}_y \]
\[ = \;\; x \cdot \begin{pmatrix}1 \\ 0\end{pmatrix} + y \cdot \begin{pmatrix}0 \\ 1\end{pmatrix} \]
Die Vektoren \(\vec{e}_x\) und \(\vec{e}_y\) spannen die \(x,y\)-Ebene auf.
Beispiel
Finde die Linearkombination der beiden Vektoren \(\vec{v}\) und \(\vec{w}\), die den Ortsvektor \(\overrightarrow{0P}\) von \(P(3,3)\) bilden.
\[ \vec{v}=\begin{pmatrix}1\\-1\end{pmatrix}, \quad \vec{w}=\begin{pmatrix}5\\1\end{pmatrix} \]
Wir setzen die Linearkombination mit den beiden unbekannten Parametern \(k\) und \(l\) auf:
\[ k \cdot \vec{v} + l \cdot \vec{w} = \overrightarrow{0P} \]
\[ k \cdot \begin{pmatrix}1 \\ -1\end{pmatrix} + l \cdot \begin{pmatrix}5 \\ 1\end{pmatrix} = \begin{pmatrix}3 \\ 3\end{pmatrix} \]
Jetzt schauen wir einmal nur die erste Zeile für die \(x\)-Komponente an. Sie gibt uns eine Gleichung mit den beiden Unbekannten \(k\) und \(l\):
\[ k \cdot 1 + l \cdot 5 = 3 \]
Die zweite Zeile gibt analog:
\[ k \cdot (-1) + l \cdot 1 = 3 \]
Wenn wir in dieser zweiten Gleichung \(k\) addieren und \(3\) subtrahieren, erhalten wir \(k = l-3\). Wir können deshalb statt \(k\) auch \((l-3)\) schreiben, weil sie gleich sind. Wir gehen deshalb in die erste Gleichung und ersetzen das \(k\) mit \((l-3)\):
\[ (l-3) \cdot 1 + l \cdot 5 = 3 \]
Jetzt vereinfachen wir die Gleichung und erhalten, lösen sie für \(l\) auf und erhalten:
\[ l – 3 + 5l = 3 \quad \rightarrow \quad \underline{l = 1}\]
Nun kennen wir \(l\) und wissen, dass \(k=l-3\), d.h. \(\underline{k=-2}\). Wir kontrollieren die Linearkombination:
\[ (-2) \cdot \begin{pmatrix}1 \\ -1\end{pmatrix} + 1 \cdot \begin{pmatrix}5 \\ 1\end{pmatrix} \]
\[ = \begin{pmatrix}(-2) \cdot 1 + 1 \cdot 5 \\ (-2) \cdot (-1) + 1 \cdot 1\end{pmatrix} = \begin{pmatrix}3 \\ 3\end{pmatrix} \]
Das Resultat stimmt tatsächlich. Wir müssen also zwei Mal den Vektor \(\vec{v}\) subtrahieren und einmal den Vektor \(\vec{w}\) addieren und erhalten so den Ortsvektor \(\overrightarrow{0P}\). Grafisch sieht das dann so aus:
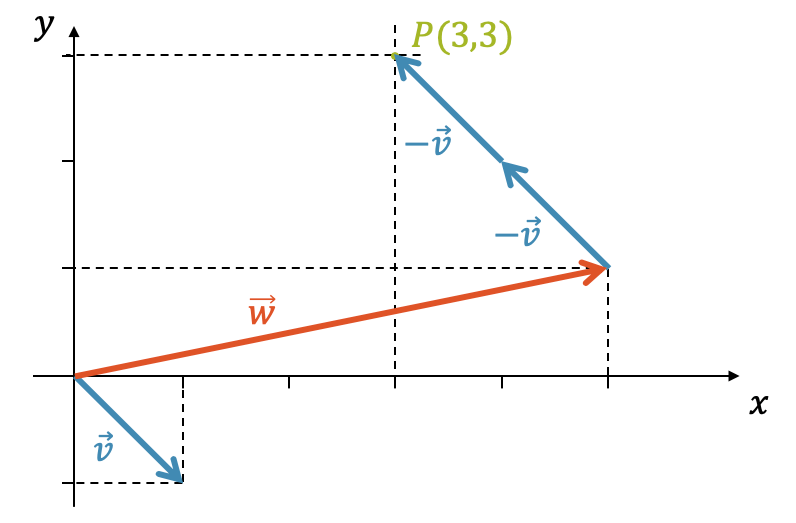
Es sieht zwar umständlich aus, aber unsere Erkenntnis aus dem obigen Beispiel ist, dass wir den Punkt \(P\) und eigentlich jeden Punkt in der \(x,y\)-Ebene mit einer Linearkombination von \(\vec{v}\) und \(\vec{w}\) erreichen können. Somit spannen \(\vec{v}\) und \(\vec{w}\) die \(x,y\)-Ebene auf, genauso wie die beiden Einheitsvektoren \(\vec{e}_x\) und \(\vec{e}_y\).
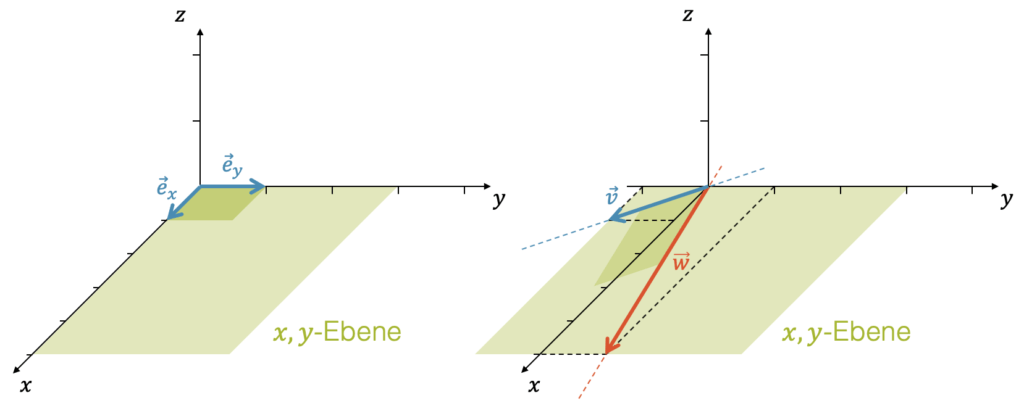
Beachte noch, dass der grosse Vorteil von \(\vec{e}_x\) und \(\vec{e}_y\) ist, dass wir die Koeffizienten \(k\) und \(l\) der Linearkombination einfach aus den Koordinaten des Zielpunkts nehmen können. Wenn wir also den Punkt \(P(3,3)\) erreichen möchten, heisst es einfach:
\[ \overrightarrow{0P} = \begin{pmatrix}3 \\ 3 \end{pmatrix} = 3 \cdot \vec{e}_x + 3 \cdot \vec{e}_y \]
Mit den beiden Vektoren \(\vec{v}\) und \(\vec{w}\) ist die Sache weniger praktisch. Niemals hätten wir einfach so raten können, dass aus dem Zahlenpar \((3,3)\) das Zahlenpaar \((-2,1)\) entstehen würde:
\[ \overrightarrow{0P} = \begin{pmatrix}3 \\ 3 \end{pmatrix} = (-2) \cdot \vec{v} + 1 \cdot \vec{w} \]
Wenn die beiden, fast willkürlich gewählten Vektoren \(\vec{v}\) und \(\vec{w}\) die \(x,y\)-Ebene aufspannen, dann könnte man annehmen, dass jedes Paar von zwei Vektoren das tut. Nicht ganz. Es gibt Vektorenpaare, die das nicht schaffen.
Beispiel
Mit welcher Linearkombination von \(\vec{v}=\begin{pmatrix}1\\-1\end{pmatrix}\) und \(\vec{t}=\begin{pmatrix}-3\\3\end{pmatrix}\) erhalten wir \(\overrightarrow{0P} = \begin{pmatrix}3 \\ 3 \end{pmatrix}\)?
Wir gehen wieder gleich vor und stellen die Linearkombination mit den beiden Unbekannten \(k\) und \(l\) auf:
\[ k \cdot \vec{v} + l \cdot \vec{t} = \overrightarrow{0P} \]
\[ k \cdot \begin{pmatrix}1 \\ -1\end{pmatrix} + l \cdot \begin{pmatrix}-3 \\ 3\end{pmatrix} = \begin{pmatrix}3 \\ 3\end{pmatrix} \]
Das gibt uns zwei Gleichungen:
\[ k = 3l + 3 \]
\[ k = 3l – 3 \]
Hier stellt sich ein Problem ein. Es gibt kein \(k\) und kein \(l\), so dass beide Gleichungen gleichzeitig erfüllt sind. Wir können die beiden rechten Seiten gleichsetzen, da sie beide \(k\) sind und erhalten die unmögliche Gleichung:
\[ 3l + 3 \stackrel{?}{=} 3l – 3 \]
Es gibt keine Linearkombination und wir erreichen den Punkt \(P\) nie mit den beiden Vektoren \(\vec{v}\) und \(\vec{t}\)!
Grafisch sieht man sofort, dass die beiden Vektoren kollinear sind und wir uns somit vom Ursprung aus nur auf der Geraden \(g\) bewegen können. Die Vektoren \(\vec{v}\) bzw. \(\vec{t}\) für sich, spannen nur die gleiche Gerade auf. Der Punkt \(P\) liegt nicht auf der Geraden und ist deshalb nicht erreichbar.
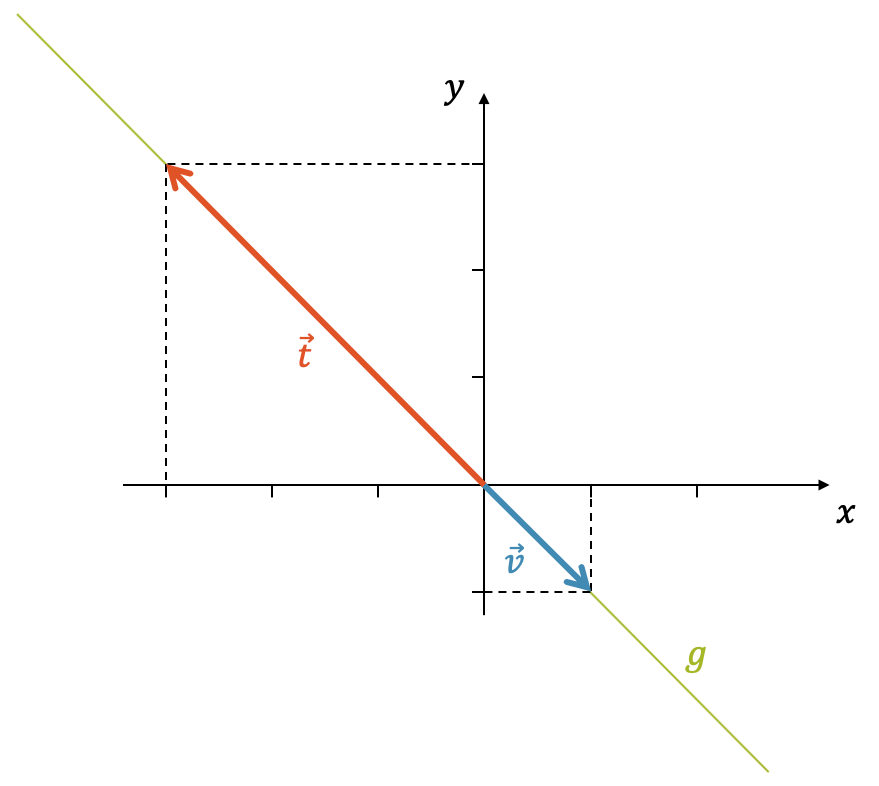
Zwei kollineare Vektoren heissen linear abhängig. Sie spannen keine Ebene auf.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.