Punkt und Ebene

Punkt auf der Ebene

Mit der folgenden Ebenengleichung erreichen wir alle Punkte \(Q\) auf der Ebene \(E\). Dazu haben wir zwei “Stellschrauben”, die beiden Parameter \(\lambda_1\) und \(\lambda_2\), die sämtliche Werte annehmen können:

\[ \overrightarrow{OQ} \;\; = \;\; \overrightarrow{OA} \; + \; \lambda_1 \cdot \vec{a_1} \; + \; \lambda_2 \cdot \vec{a_2}\]

Jetzt möchten wir aber wissen, ob ein ganz bestimmter Punkt \(P(P_x,P_y)\) auf der Ebene \(E\) ist, oder nicht. Wir nehmen seinen Ortsvektor und setzen ihn mit der Ebenengleichung gleich. Danach lösen wir die Gleichung für \(\lambda_1\) und \(\lambda_2\):

\[ \overrightarrow{OA} \; + \; \lambda_1 \cdot \vec{a_1} \; + \; \lambda_2 \cdot \vec{a_2} \; \stackrel{!}{=} \; \overrightarrow{OP} \quad \rightarrow \quad (\lambda_1,\lambda_2) \]

Mit diesen beiden Parameterwerten erreichen wir den Punkt \(P\).

Abstand zwischen Punkt und Ebene

Ist der Punkt \(P\) nicht in der Ebene \(E\), so hat er einen bestimmten Abstand \(d\) zur Ebene \(E\), den wir berechnen können. Wir schauen uns dazu die beiden Punkte \(A \in E\), \(P \notin E\) und die Ebene \(E\) von der Seite an:

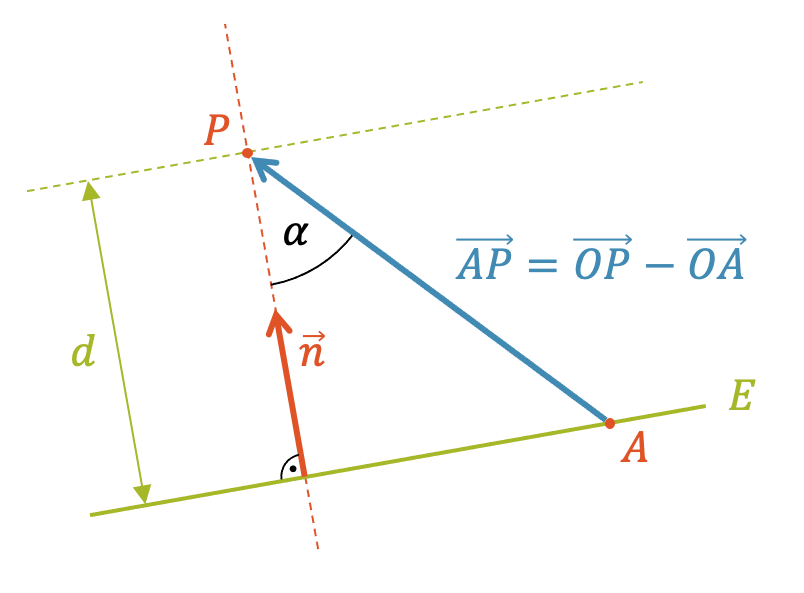
Obwohl es sich um eine räumliche Geschichte handelt, können wir die beiden Punkte \(A\) und \(P\) in unsere Zeichenebene legen. Zuerst legen wir \(P\) in unsere Zeichenebene. Dann legen wir den Normalvektor \(\vec{n}\) der Ebene ebenfalls in unsere Zeichenebene. Schliesslich drehen wir um die Achse (in Richtung von \(\vec{n}\)), bis nun auch der Punkt \(A\) in unserer Zeichenebene liegt.

Wenn \(P\) und \(A\) in der Zeichenebene liegen, dann auch ihr Verbindungsvektor \(\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\). Beachte, dass der Ursprung nicht unbedingt in der Zeichenebene sein muss.

Nun berechnen wir den Abstand \(d\) und schauen uns dazu das rechtwinklige Dreieck mit dem Winkel \(\alpha\) an. Wir können die trigonometrische Beziehung zwischen \(d\) und der Hypotenuse aufstellen:

\[ \cos(\alpha) = \frac{d}{\Big|\overrightarrow{AP}\Big|} \]

Für den Kosinus von \(\alpha\) können wir die Beziehung aus dem Skalarprodukt von \(\vec{n}\) und \(\overrightarrow{AP}\) benutzen. Er ist ja der Zwischenwinkel, zwischen den beiden Vektoren:

\[ \cos(\alpha) \;\; = \;\; \frac{\vec{n} \cdot \overrightarrow{AP}}{\big| \vec{n} \big| \cdot \Big|\overrightarrow{AP}\Big|} \]

Wir setzen beides gleich und erhalten eine Gleichung, in welcher wir den einen Betrag weg kürzen können:

\[ \require{cancel} \frac{d}{\cancel{\Big|\overrightarrow{AP}\Big|}} \;\; = \;\; \frac{\Big|\vec{n} \cdot \overrightarrow{AP}\Big|}{\big| \vec{n} \big| \cdot \cancel{\Big|\overrightarrow{AP}\Big|}} \]

Damit haben wir einen Ausdruck für den Abstand \(d\) gefunden. Da das Skalarprodukt im Zähler auch negative Werte erzeugen kann, ein negativer Abstand aber keinen Sinn machen würde, haben wir das Skalarprodukt zwischen zwei Betragsstriche gesetzt. 

Beispiel

Finde heraus, welcher der beiden Punkte \(S(2,0,-1)\) und \(T(0,3,6)\) Teil der Ebene \(E\) ist und welchen Abstand der andere Punkt von der Ebene hat.

\[ E \colon \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} \; = \; \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + \lambda_1 \cdot \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \]

---

Wir setzen die Koordinaten von \(S\) in die Gleichung der Ebene ein und schauen, ob wir ein bestimmtes Paar \(\lambda_1\) und \(\lambda_2\) finden, das zum Punkt \(S(2,0,-1)\) auf \(E\) führt.

\[ \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + \lambda_1 \cdot \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \;\; \stackrel{!}{=} \;\; \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} \]

Wir erhalten das folgende Gleichungssystem:

\[ \begin{cases} \begin{array}{cc} 0 + 2 \;\lambda_1 + 0 \;\lambda_2 = 2 \\ 1 + 0 \;\lambda_1 + 1 \;\lambda_2 = 0 \\ 0 + 1 \;\lambda_1 + 2 \;\lambda_2 = -1 \end{array} \end{cases} \]

Etwas aufgeräumt erkennen wir schon viel mehr:

\[ \begin{cases} \begin{array}{cc} 2 \;\lambda_1 = 2 \\ 1 + \lambda_2 = 0 \\  \lambda_1 + 2 \;\lambda_2 = -1 \end{array} \end{cases} \]

Aus der ersten Gleichung erhalten wir \(\lambda_1 = 1\) und aus der zweiten Gleichung \(\lambda_2=-1\). Dann schauen wir, ob die dritte Gleichung mit dieser Lösung einverstanden ist:

\[ \lambda_1+2\lambda_2=1+2 \cdot (-1)=-1 \]

Die dritte Gleichung ist erfüllt, d.h. \(S \in E\).

Für den zweiten Punkt \(T\) wissen wir aus der Aufgabenstellung, dass er nicht in \(E\) ist, wenn \(S\) schon Teil der Ebene ist, d.h. wir versuchen gar nicht das Gleichungssystem zu lösen, sondern gehen gleich zur Berechnung des Abstands über. Dazu brauchen wir einen Normalvektor \(\vec{n}\) zu \(E\). Den erhalten wir natürlich, indem wir die beiden die Ebene aufspannenden Vektoren \(a_1\) und \(a_2\) mit einem Vektorprodukt kombinieren. Beachte, dass die Länge von \(\vec{n}\) nicht relevant ist, da die Formel den Einheitsvektor von \(\vec{n}\) benutzt (Vektor mit gleicher Richtung, aber Länge 1):

\[ \frac{\vec{n}}{\big|\vec{n}\big|} \]

\[ \vec{n} = \vec{a_1} \times \vec{a_2} = \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} \times \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -1 \\ -4 \\ 2 \end{pmatrix} \]

Dann brauchen wir noch die Länge von \(\vec{n}\):

\[ \big| \vec{n} \big| = \sqrt{(-1)^2+(-4)^2+2^2} = \sqrt{1+16+4} = \sqrt{21} \]

Jetzt schauen wir unsere hergeleitete Formel für den Abstand \(d\) an. Wir brauchen den Verbindungsvektor zwischen dem Punkt \(T\) und dem Punkt \(A\) auf der Ebene:

\[ \overrightarrow{OT} = \begin{pmatrix} 0 \\ 3 \\ 6 \end{pmatrix}, \quad \overrightarrow{OA} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \]

\[ \overrightarrow{OT} – \overrightarrow{OA} = \begin{pmatrix} 0-0 \\ 3-1 \\ 6-0 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 6 \end{pmatrix} \]

Damit haben wir alles, was wir brauchen:

\[ d = \frac{\vec{n}}{\big| \vec{n} \big|} \cdot \Big(\overrightarrow{OT}-\overrightarrow{OA}\Big) = \frac{1}{\sqrt{21}} \cdot \begin{pmatrix} -1 \\ -4 \\ 2 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 2 \\ 6 \end{pmatrix} \]

\[ d = \frac{1}{\sqrt{21}} \cdot \Big( (-1) \cdot 0 + (-4) \cdot 2 + 2 \cdot 6 \Big) = \frac{4}{\sqrt{21}} \approx \underline{0.873} \]