Spatprodukt

Das Spatprodukt ist ein gemischtes Produkt, denn es vereint das Skalarprodukt und das Vektorprodukt in einem. Die Bezeichnung “Spat” geht auf die Minerale Feldspat und Kalkspat zurück, deren schiefwinklige Kristalle dem typischen Spatvolumen entsprechen, das sich mit dem Spatprodukt berechnen lässt.

Für das Spatprodukt gibt es verschiedene Definitionen und Schreibweisen. Eine davon ist die Folgende mit eckigen Klammern:

Das Resultat des Spatprodukts ist eine Zahl, denn es handelt sich um ein Skalarprodukt von zwei Vektoren, wobei der zweite Vektor aus einem Vektorprodukt stammt.

Die Bedeutung des Resultats des Spatprodukts ist ähnlich zur Fläche des Parallelogramms beim Vektorprodukt: Es entspricht dem Volumen des sog. Spats, einem Parallelepiped, dass durch die drei Vektoren aufgespannt wird. Zur Veranschaulichung nehmen wir die Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\)

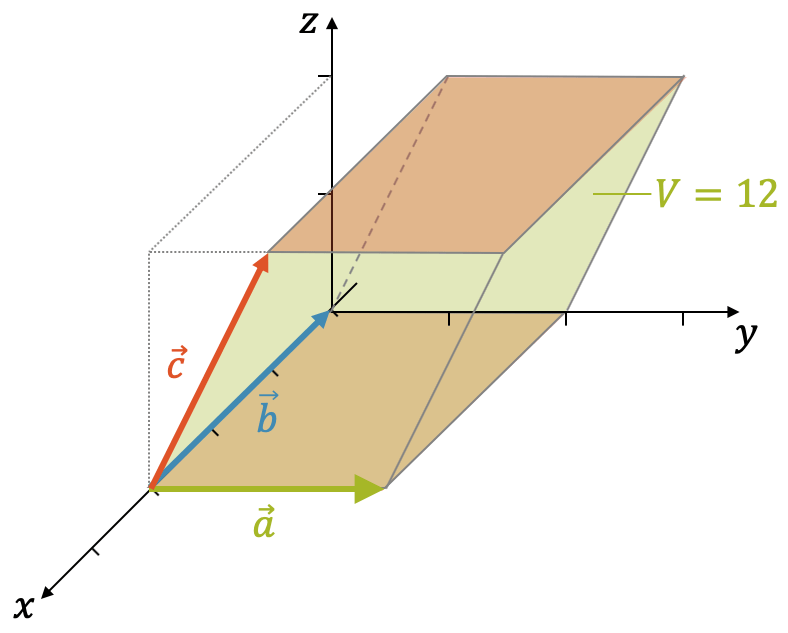
Beachte, dass die Grundfläche des Spats in diesem Beispiel ein Rechteck ist, denn die Vektoren \(\vec{a}\) und \(\vec{b}\) stehen senkrecht aufeinander. Ihre Beträge sind \(|\vec{a}|=2\) und \(|\vec{b}|=3\), so dass die Rechteckfläche \(A = 2 \cdot 3\) beträgt. Über dieser Rechteckfläche, auf einer Höhe \(h=2\), “schwebt” wieder die gleiche Rechteckfläche. Wäre es ein Quader, so könnten wir das Volumen einfach durch “Fläche mal Höhe” berechnen.

Tatsächlich können wir das auch dann tun, wenn wir das Volumen des Spats berechnen möchten. Wir erinnern uns an die Fläche des Parallelogramms, die der “Grundseite mal Höhe” entsprach. Es kam nicht darauf an, welchen Winkel das Parallelogramm hatte. Das Rechteck, als spezielles Parallelogramm hat die gleiche Fläche. Hier verhält es sich gleich: Der (rechteckige) Quader hat das gleiche Volumen wie der schiefwinklige Spat. Einziges Kriterium ist die Höhe, denn das Volumen berechnet sich als “Grundfläche mal Höhe”.

Die Höhe beträgt in unserem Fall \(2\). Die Grundfläche ist in der \(x,y\)-Ebene und die dazu senkrechte Höhe ist parallel zur \(z\)-Achse. Der Vektor \(\vec{c}\) hat eine \(z\)-Komponente von \(2\), so dass die zweite Rechteckfläche in einer Höhe von \(2\) über der Grundfläche “schwebt”. Das Volumen des Spats beträgt in unserem Fall also:

\[ V = A \cdot h = (2 \cdot 3) \cdot 2 = 12 \]

Tatsächlich entspricht das Volumen des Spats dem gleichen Betrag, den wir auch mit dem Spatprodukt erhalten haben. Was passiert jetzt, wenn wir die Reihenfolge der Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) ändern? Wenn wir die beiden Vektoren \(\vec{b}\) und \(\vec{c}\) vertauschen, die im Vektorprodukt stecken, ändert das Vektorprodukt sein Vorzeichen und somit auch das Spatprodukt. Wir müssen beim Spatprodukt deshalb unbedingt die Reihenfolge einhalten. Gewisse Vertauschungen sind erlaubt, solange sie der zyklischen Permutation folgen, denn das Spatprodukt ist ein Rechtssystem:

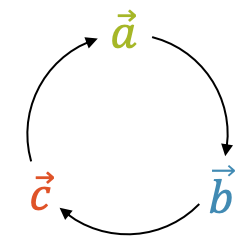
\[ [ \; \vec{a} \; \vec{b} \; \vec{c} \; ] = [ \; \vec{b} \; \vec{c} \; \vec{a} \; ] = [ \; \vec{c} \; \vec{a} \; \vec{b} \; ] \;\; = \;\; 12 \]

Eine Vertauschung von nur zwei Vektoren ändert das System zu einem Linkssystem und somit ändert das Vorzeichen des Spatprodukts. Der Betrag davon ist natürlich immer noch gleich \(12\), da sich an den aufspannenden Vektoren und damit am Volumen des Spats nichts geändert hat.

\[ [ \; \vec{a} \; \vec{c} \; \vec{b} \; ] = [ \; \vec{c} \; \vec{b} \; \vec{a} \; ] = [ \; \vec{b} \; \vec{a} \; \vec{c} \; ] \;\; = \;\; -12 \]

Kann das Spatprodukt auch null ergeben? Ja, wenn einer der Vektoren ein Nullvektor ist, aber das wäre uninteressant. Das Spatprodukt kann aber auch in anderen Fällen null werden.

Wenn zwei der Vektoren kollinear sind, dann spannen sie mit dem dritten Vektor bloss ein (flaches) Parallelogramm auf, das kein Volumen hat. Das Spatprodukt ist somit null.

Das Volumen des Spatprodukts kann auch dann null sein, wenn die drei Vektoren komplanar sind, denn sie liegen in einer gemeinsamen Ebene und können deshalb kein Spatvolumen aufspannen. Der Spat liegt flach in der gemeinsamen Ebene.

---

Beispiel

Zeige, dass die drei folgenden Vektoren in der gleichen räumlichen Ebene liegen:

\[ \vec{u} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \quad \vec{v} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix}, \quad \vec{w} = \begin{pmatrix} 4 \\ 3 \\ 5 \end{pmatrix} \]

Wenn drei Vektoren komplanar sind, dann verschwindet ihr Spatprodukt. Das Vorzeichen des Spatprodukts spielt keine Rolle (da es ja null sein soll) und deshalb können wir das Spatprodukt mit einer beliebigen Reihenfolge bilden. Wir wählen \([\vec{u} \; \vec{v} \; \vec{w} ]\) und rechnen zuerst das Vektorprodukt \((\vec{u} \times \vec{v})\):

\[ \vec{v} \times \vec{w} \;\; = \;\; \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} \times \begin{pmatrix} 4 \\ 3 \\ 5 \end{pmatrix} \]

\[ = \begin{pmatrix} 1 \cdot 5 – 2 \cdot 3 \\ 2 \cdot 4 – 3 \cdot 5 \\ 3 \cdot 3 – 1 \cdot 4 \end{pmatrix} = \begin{pmatrix} -1 \\ -7 \\ 5 \end{pmatrix} \]

Jetzt bilden wir das Skalarprodukt mit dem Vektor \(\vec{u}\):

\[ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} -1 \\ -7 \\ 5 \end{pmatrix} \]

\[ = 1 \cdot (-1) + 2 \cdot (-7) + 3 \cdot 5 \]

\[ = (-1) -14 + 15 = \underline{\; 0 \;} \]

Das Spatprodukt verschwindet, womit bewiesen ist, dass die drei Vektoren \(\vec{u}\), \(\vec{v}\) und \(\vec{w}\) in der gleichen ebene liegen, also komplanar sind.