Ebene und Ebene

Zwei Ebenen werden sich im Normalfall in einer Geraden schneiden. Sie können aber auch parallel sein oder sogar identisch, d.h. aufeinander liegen.

Wenn zwei Ebenen parallel sind, reicht es aus, den Abstand eines Punkt auf der einen Ebene mit der zweiten Ebene zu berechnen. Damit erhalten wir automatischen den Abstand der beiden Ebenen.

Für den etwas interessanteren Fall, in welchem sich zwei Ebenen schneiden, schauen wir uns ein paar Beispiele an:

Beispiel

Finde die Gleichung der Schnittgeraden der beiden Ebenen \(E_1\) und \(E_2\).

\[ E_1 \colon \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} + \lambda_1 \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 1 \\ 4 \\ 0 \end{pmatrix} \]

\[ E_2 \colon \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} + \lambda_3 \cdot \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix} + \lambda_4 \cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} \]

---

Wir suchen die Schnittmenge der beiden Ebenen, d.h. diejenigen Punkte, die von beiden Ebenengleichungen gleichzeitig erfüllt werden. Dazu setzen wir die beiden Ebenengleichungen gleich:

\[ \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} + \lambda_1 \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 1 \\ 4 \\ 0 \end{pmatrix} \]

\[ \stackrel{!}{=} \;\; \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} + \lambda_3 \cdot \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix} + \lambda_4 \cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} \]

Nach etwas Umformen erhalten wir ein Gleichungssystem mit den vier Unbekannten \(\lambda_1\), \(\lambda_2\), \(\lambda_3\) und \(\lambda_4\). Die vierte Unbekannte \(\lambda_4\) haben wir auf die rechte Seite genommen, denn eigentlich reichen uns drei Unbekannte für ein Gleichungssystem mit drei Gleichungen:

\[ \begin{cases} \begin{array}{cc} 2 \lambda_1 + \lambda_2 – \lambda_3 \;\; = \;\; 2 \lambda_4 – 1 \\ 4 \lambda_2 + 2 \lambda_3 \;\; = \;\; \lambda_4 + 1 \\  -\lambda_3 \;\; = \;\; 0 \\ \end{array} \end{cases} \]

Wir werden die Unbekannte \(\lambda_4\) als Parameter behandeln und nicht mehr als Unbekannte, d.h. wir kennen den Wert von \(\lambda_4\) nicht, müssen ihn aber auch nicht kennen. Es wird die “Stellschraube” sein, die wir für die Gleichung der Geraden brauchen werden. Um dies zu verdeutlichen, taufen wir \(\lambda_4\) in \(s\) um:

\[ \begin{cases} \begin{array}{cc} 2 \lambda_1 + \lambda_2 – \lambda_3 \;\; = \;\; 2 s – 1 \\ 4 \lambda_2 + 2 \lambda_3 \;\; = \;\; s + 1 \\ -\lambda_3 \;\; = \;\; 0 \\ \end{array} \end{cases} \]

Die erste Lösung ist offensichtlich: \(\underline{\lambda_3=0}\)

Aus der zweiten Gleichung erhalten wir: \(\underline{\lambda_2=\frac{1}{4}s+\frac{1}{4}}\)

Die Lösung für \(\lambda_1\) erhalten wir, indem wir aus den ersten beiden Gleichungen ein Gleichungssystem bilden und dieses mit dem Gauss’schen Additionsverfahren lösen:

\[ \begin{cases} 4 \lambda_2 \;\; = \;\; s + 1 \\ 2 \lambda_1 + \lambda_2 \;\; = \;\; 2s-1 \end{cases} \]

\[ \begin{array}{cc} 4 \lambda_2 \;\; = \;\; s + 1 \\ -8 \lambda_1 – 4 \lambda_2 \;\; = \;\; -8s + 4 \\ \hline -8 \lambda_1 \;\; = \;\; -7s + 5 \end{array} \]

Das gibt uns die Lösung:

\[ \underline{\lambda_1=\frac{7}{8}s-\frac{5}{8}} \]

Wir haben jetzt die beiden Ebenengleichungen gleichgesetzt und die Lösungen für die drei Unbekannten \(\lambda_1\), \(\lambda_2\) und \(\lambda_3\) gefunden. Für die Beschreibung der Schnittmenge, können wir jetzt eine der beiden Ebenengleichungen nehmen und unsere Lösungen für die \(\lambda_i\) einsetzen. Am einfachsten ist die Gleichung von \(E_2\), wo wir \(\lambda_3=0\) und \(\lambda_4=s\) einsetzen: 

\[ \require{cancel} \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} + \cancel{0 \cdot \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix}} + s \cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} \]

Das ist bereits schon die Parameterform der Schnittgeraden \(g\) beider Ebenen:

\[ g \colon \;\; \underline{\begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}} \]

Rein aus Neugierde schauen wir mal, ob es auch mit der Gleichung von \(E_1\) gehen würde. Hier setzen wir die Lösungen \(\;\lambda_1=\frac{7}{8}s-\frac{5}{8}\;\) und \(\;\lambda_2=\frac{1}{4}s+\frac{1}{4}\;\) ein:

\[ \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} + \Big(\frac{7}{8}s-\frac{5}{8}\Big) \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} + \Big(\frac{1}{4}s+\frac{1}{4}\Big) \cdot \begin{pmatrix} 1 \\ 4 \\ 0 \end{pmatrix} \]

Diese Vektorgleichung kann als drei Gleichungen für die drei Koordinaten \(x\), \(y\) und \(z\) aufgeschrieben werden:

\[ \begin{cases} x: \quad 1 + \frac{7}{4} s – \frac{5}{4} + \frac{1}{4} s + \frac{1}{4} \; = \; 2s \\ y: \quad 1 + s + 1 \; = \; s + 2 \\ z: \quad 0 \; = \; 0 \end{cases} \]

Damit haben wir eigentlich folgendes erhalten, was wieder der gleichen Geradengleichung entspricht:

\[ \begin{pmatrix} x \\ y \\ z \end{pmatrix} \;\; = \;\; \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} \]

Beispiel

Finde die Gleichung der Schnittgeraden \(g\), die durch den Schnitt beider Ebenen \(E_1\) und \(E_2\) entsteht:

\[ E_1 \colon \;\; x + y + z = 1 \]

\[ E_2 \colon \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} + \lambda_3 \cdot \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix} + \lambda_4 \cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} \]

---

Eine Möglichkeit ist, die beiden Gleichungen gleichzusetzen. Das tun wir, indem wir aus der Vektorgleichung von \(E_2\) die Ausdrücke für \(x\), \(y\) und \(z\) in die Gleichung von \(E_1\) einsetzen:

\[ \begin{array}{ll} x = \lambda_3 + 2 \lambda_4 \\ y = 2 – 2 \lambda_3 + \lambda_4 \\ z = \lambda_3 \end{array} \]

\[ x + y + z = (\lambda_3 + 2 \lambda_4) + (2 – 2 \lambda_3 + \lambda_4) + (\lambda_3) \;\; = \;\; 1 \]

\[ \require{cancel} \cancel{\lambda_3} + 2 \lambda_4 + 2 – \cancel{2 \lambda_3} + \lambda_4 + \cancel{\lambda_3} \;\; = \;\; 1 \]

\[ 3\lambda_4 = -1 \quad \rightarrow \quad \lambda_4 = -\frac{1}{3} \] 

Wenn wir das oben wieder einsetzen und \(\lambda_3\) zu unserem Parameter machen, d.h. \(\lambda_3=s\), erhalten wir die Geradengleichung mit dem Parameter \(s\):

\[ \begin{pmatrix} x \\ y \\ z \end{pmatrix} \;\; = \;\; \begin{pmatrix} s + 2 \cdot \big(-\frac{1}{3}\big) \\ 2-2s+\big(-\frac{1}{3}\big) \\ s \end{pmatrix} = \underline{\begin{pmatrix} -\frac{2}{3} \\ \frac{5}{3} \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix}} \]

Beispiel

Finde den Richtungsvektor der Schnittgeraden von \(E_1\) und \(E_2\) (aus dem ersten Beispiel), indem du zwei Normalvektoren findest und für diese dann ein Vektorprodukt bildest.

\[ E_1 \colon \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} + \lambda_1 \cdot \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 1 \\ 4 \\ 0 \end{pmatrix} \]

\[ E_2 \colon \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} + \lambda_3 \cdot \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix} + \lambda_4 \cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} \]

---

Den Normalvektor erhalten wir, indem wir die beiden Richtungsvektoren \(a_1\) und \(a_2\), die die Ebene aufspannen, in einem Vektorprodukt mit einander multiplizieren. Das Resultat steht ja senkrecht auf beiden erzeugenden Vektoren und damit auf der Ebene.

\[ \vec{n_1} = \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} \times \begin{pmatrix} 1 \\ 4 \\ 0 \end{pmatrix} = \begin{pmatrix} -4 \\ 1 \\ 8 \end{pmatrix} \]

\[ \vec{n_2} = \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix} \times \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} -1 \\ 2 \\ 5 \end{pmatrix} \]

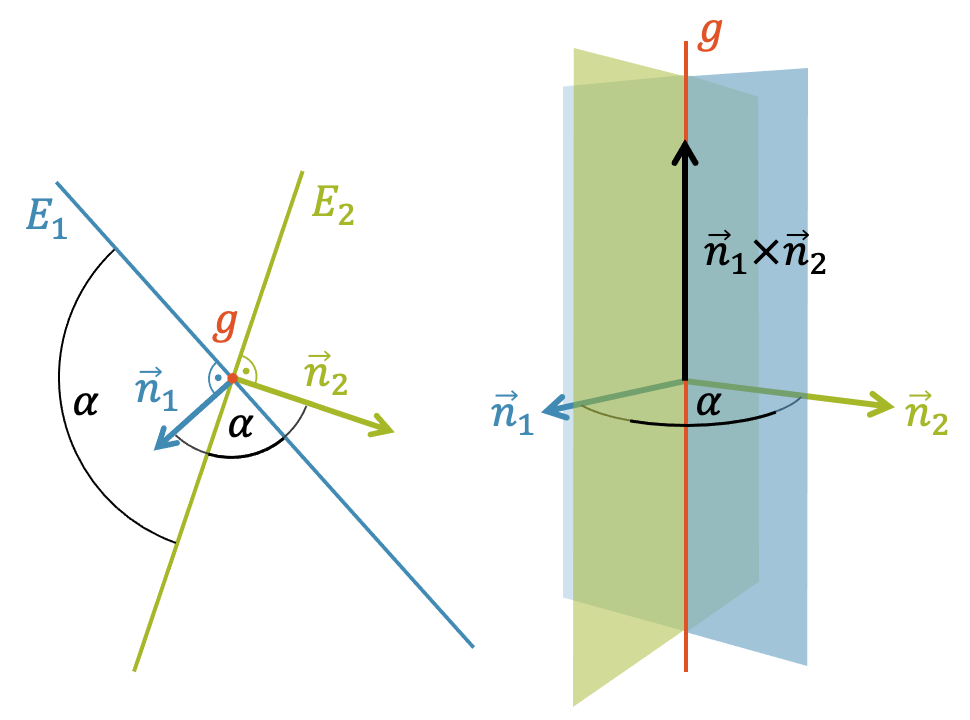
Wir haben jetzt zwei Vektoren, die normal auf den beiden sich schneidenden Ebenen liegen. Wenn wir diese beiden Vektoren im Vektorprodukt mit einander multiplizieren, kriegen wir einen Vektor, der senkrecht auf diesen beiden Vektoren liegt. Dieser Vektor zeigt in Richtung der Schnittgeraden.

\[ \vec{n_1} \times \vec{n_2} = \begin{pmatrix} -4 \\ 1 \\ 8 \end{pmatrix} \times \begin{pmatrix} -1 \\ 2 \\ 5 \end{pmatrix} = \underline{\begin{pmatrix} -11 \\ 12 \\ -7 \end{pmatrix}} \]