Gleichung einer Geraden

Parameterform

Wir werden uns jetzt anschauen, wie eine Gerade mit Hilfe der Vektorgeometrie beschrieben werden kann. Die Vektorgeometrie ist hier besonders stark, weil sie leicht von der zweidimensionalen Welt in die dreidimensionale Welt erweitert werden kann, d.h. wir werden hier lernen Geraden im Raum zu beschreiben.

Als Erstes sollten wir uns daran erinnern, was eine Gerade eigentlich ist. Es ist eigentlich eine Reihe von unendlich vielen Punkten mit einer bestimmten mathematischen Eigenschaft, die macht, dass sie alle auf einer geraden Linie zu liegen. Die Punkte \(A\), \(B\), \(C\) und \(D\) sind ein paar Beispiele davon.

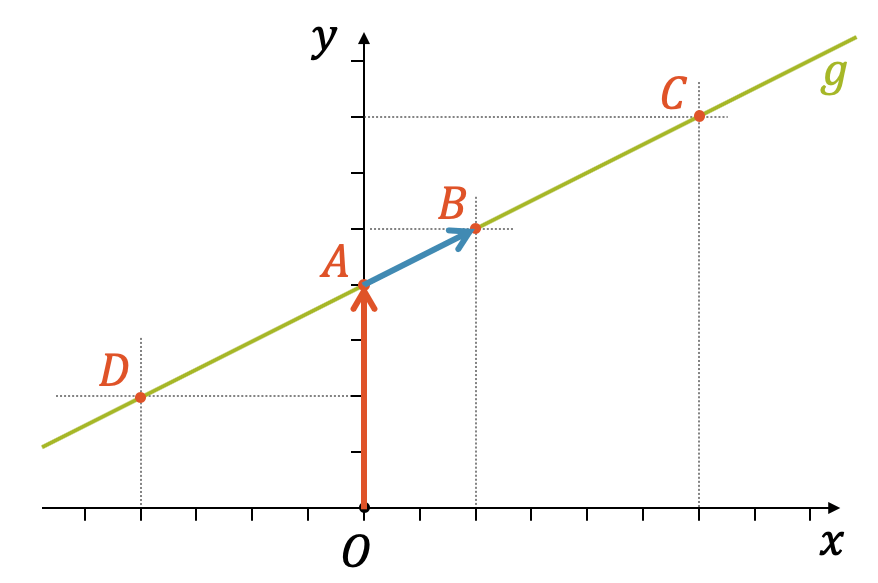
Unser Ziel ist die mathematische Beschreibung aller Punkte auf der Geraden \(g\). Der erste Punkt \(A\) kann einfach beschrieben werden. Wir kennen seine Koordinaten \(A(0,4)\) und somit erreichen wir den Punkt einfach durch den Ortsvektor \(\overrightarrow{OA}\):

\[ \overrightarrow{OA} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} \]

Jetzt schauen wir uns den zweiten Punkt \(B\) an. Natürlich könnten wir den auch über die Koordinaten von \(B\) definieren. Wir wählen aber einen anderen Weg, der vielleicht jetzt ein bisschen umständlich aussieht, dessen Nutzen wir aber gleich anschliessend erkennen werden:

\[ \overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB} \]

Den Vektor \(\overrightarrow{OA}\) haben wir bereits. Den anderen Vektor \(\overrightarrow{AB}\) erhalten wir folgendermassen:

\[ \overrightarrow{AB} = \overrightarrow{OB} – \overrightarrow{OA} \]

\[ = \begin{pmatrix} 2 – 0 \\ 5 – 4 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} \]

Wie erreichen wir den Punkt \(C\)? Da \(C\) auf der Geraden liegt, müssen wir nur in \(A\) auf die Gerade gehen und von da an uns in der Richtung der Geraden uns bewegen. Dieses Richtung gibt uns der Vektor \(\overrightarrow{AB}\) vor. Wir haben mit \(A\) einen Startpunkt auf der Geraden und mit \(\overrightarrow{AB}\) einen Vektor, der die Richtung der Geraden vorgibt. Den Punkt \(C\) erreichen wir jetzt, wenn wir den Vektor \(\overrightarrow{AB}\) dreimal addieren:

\[ \overrightarrow{OC} = \overrightarrow{OA} + 3 \cdot \overrightarrow{AB} \]

Wir führen die Rechnung aus und kontrollieren, ob die erhaltenen Koordinaten, denjenigen von \(C\) entsprechen:

\[ \overrightarrow{OC} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} + 3 \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} \]

\[ = \begin{pmatrix} 0 + 3 \cdot 2 \\ 4 + 3 \cdot 1 \end{pmatrix} = \begin{pmatrix} 6 \\ 7 \end{pmatrix}\]

Tatsächlich hat der Punkt \(C\) die Koordinaten \(C(6,7)\). Schliesslich ermitteln wir die Koordinaten des Punkts \(D\), indem wir, ausgehend von \(A\) zweimal den Vektor \(\overrightarrow{AB}\) subtrahieren oder das \((-2)\)-fache addieren: 

\[ \overrightarrow{OD} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} + (-2) \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} \]

\[ = \begin{pmatrix} 0 – 2 \cdot 2 \\ 4 – 2 \cdot 1 \end{pmatrix} = \begin{pmatrix} -4 \\ 2 \end{pmatrix} \]

Somit hat der Punkt \(D\) die Koordinaten \(D(-4,2)\), was wir im Koordinatensystem oben bestätigen können. Jetzt können wir die Sache verallgemeinern und sagen, dass wir vom Punkt \(A\) ausgehend, alle Punkte der Geraden \(g\) erreichen können, indem wir ein Vielfaches (und dazu nehmen wir einfach den Faktor \(\lambda\)) von \(\overrightarrow{AB}\) addieren. Der Vektor \(\overrightarrow{AB}\) zeigt in Richtung von \(g\) und alle Vielfachen somit auch. Sie sind aber beliebig kurz oder lang. Damit lassen sich alle Punkte von \(A\) in einer Richtung der Geraden \(g\) erreichen. Für die entgegengesetzte Richtung brauchen wir nur ein negatives Vielfaches (\(\lambda < 0\)).

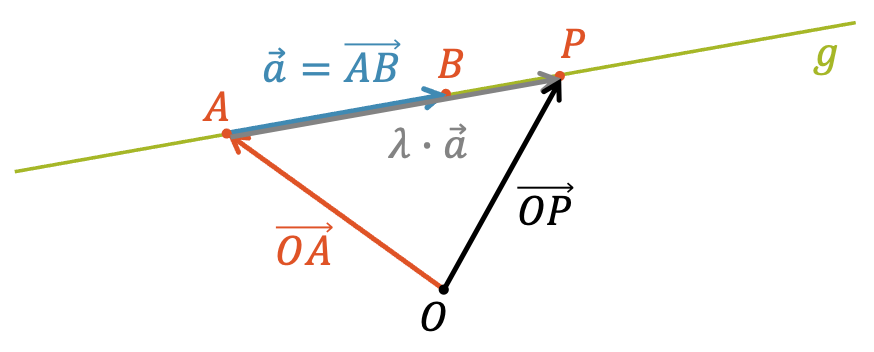
Alle Punkte \(P\) einer Geraden \(g\) mit den beiden Punkten \(A \in g\) und \(B \in g\) kann beschrieben werden durch eine Vektorgleichung, eigentlich ein Gleichungssystem von drei Gleichungen, je eine Gleichung pro Koordinate.

Der Vektor \(\vec{a}\) verläuft parallel zur Geraden \(g\), d.h. er verkörpert die Richtung der Geraden, weshalb ich ihn Richtungsvektor der Geraden nenne.

Der reelle Parameter \(\lambda\) (positiv oder negativ) bestimmt, welchen Punkt \(P\) von \(A\) aus erreicht wird, denn wir addieren einen mit \(\lambda\) gestreckten Richtungsvektor \(\vec{a}\) zum Ortsvektor von \(A\).

Beispiel

Gegeben ist die folgende Geradengleichung für \(g\). Überprüfe, ob die Punkte \(E(3,5,7)\) und \(F(-1,-3,1)\) auf der Geraden \(g\) sind oder nicht.

\[ g \colon \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} \]

---

Wenn \(E\) auf der Geraden ist, dann gibt es ein \(\lambda\) für welches wir die Geradengleichung aufstellen können, d.h. wir müssen einfach das \(\lambda\) finden und überprüfen, ob mit diesem der Punkt \(E\) erreicht werden kann. Wir stellen deshalb die Geradengleichung auf und setzen sie gleich mit dem Ortsvektor des Punkts \(E\):

\[ \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} \;\; \stackrel{!}{=} \;\; \begin{pmatrix} 3 \\ 5 \\ 7 \end{pmatrix} \]

Jetzt schauen wir uns die Komponenten der Vektoren einzeln an, d.h. wir erhalten drei Gleichungen. Eine für die \(x\)-Komponente, eine für \(y\)- und eine für die \(z\)-Komponente:

\[ x \colon \quad 0 + \lambda \cdot 1 = 3 \]

\[ y \colon \quad -1 + \lambda \cdot 2 = 5 \]

\[ z \colon \quad 1 + \lambda \cdot 2 = 7 \]

Aus der ersten Gleichung erhalten wir sofort die Lösung \(\lambda = 3\). Setzen wir diese Lösung in der zweiten und dritten Gleichung ein, so sehen wir, dass diese alle schön erfüllt sind:

\[ y \colon \quad -1 + 3 \cdot 2 \stackrel{?}{=} 5 \]

\[ z \colon \quad 1 + 3 \cdot 2 \stackrel{?}{=} 7 \]

Damit liegt der Punkt \(E\) tatsächlich auf der Geraden \(g\) und vom Startpunkt \(A(0,-1,1)\) aus, den wir aus der Geradengleichung ablesen können, mit dem Faktor \(\lambda = 3\) zu erreichen. Jetzt gehen wir gleich vor für den Punkt \(F\):

\[ \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} \;\; \stackrel{!}{=} \;\; \begin{pmatrix} -1 \\ -3 \\ 1 \end{pmatrix} \]

\[ x \colon \quad 0 + \lambda \cdot 1 = -1 \]

\[ y \colon \quad -1 + \lambda \cdot 2 = -3 \]

\[ z \colon \quad 1 + \lambda \cdot 2 = 1 \]

Wieder erhalten wir aus der ersten Gleichung den Wert für \(\lambda\): Dieses Mal beträgt er \(\lambda = -1\). Wir setzen diesen Wert in die beiden anderen Gleichungen ein…

\[ y \colon \quad -1 + (-1) \cdot 2 \stackrel{?}{=} -3 \]

\[ z \colon \quad 1 + (-1) \cdot 2 \stackrel{?}{=} 1 \]

Die Gleichung der \(y\)-Komponente ist erfüllt, aber die Gleichung der \(z\)-Komponente nicht! Der Punkt \(F\) kann die Geradengleichung nicht erfüllen und liegt deshalb nicht auf der Geraden \(g\) !

Normalform

Wir können in zwei Dimensionen eine Gerade auch durch einen Normalvektor \(\vec{n}\) beschreiben, der senkrecht auf der Geraden steht. Durch den Vektor kriegen wir die Richtung der Geraden. Zusätzlich brauchen wir noch einen Stützvektor \(\overrightarrow{OA}\), der vom Ursprung zu einem Punkt \(A\) auf der Geraden zeigt. Damit ist die Gerade vollständig beschrieben.

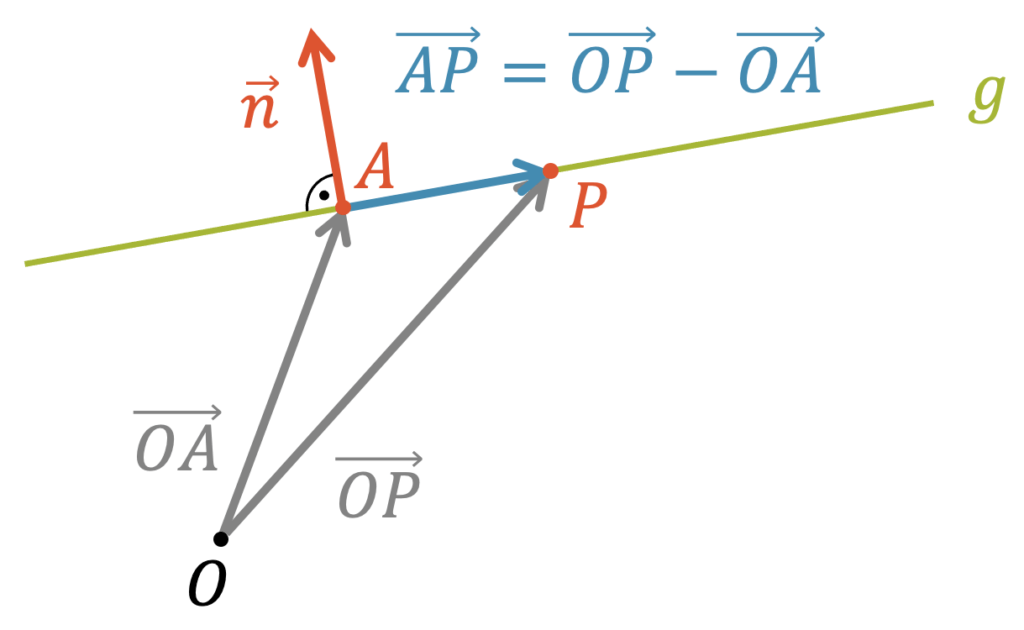
Für den Normalvektor gilt die Forderung, dass er senkrecht zu einem Vektor \(\overrightarrow{AP}\) liegt, der eine Verbindung vom Punkt \(A\) zu einem beliebigen Punkt \(P\) auf der Geraden \(g\) gibt. Senkrecht aufeinander stehende Vektoren haben ein verschwindendes Skalarprodukt, d.h.

\[ \vec{n} \perp \overrightarrow{AP} \quad \Leftrightarrow \quad \vec{n} \cdot \overrightarrow{AP} = 0 \]

Der Vektor \(\overrightarrow{AP}\) ist eigentlich die Differenz der Ortsvektoren von \(P\) und \(A\):

\[ \overrightarrow{AP} = \overrightarrow{OP} – \overrightarrow{OA} \]

Wir setzen das in die Vektorgleichung ein und erhalten:

\[ \vec{n} \cdot \big( \overrightarrow{OP} – \overrightarrow{OA} \big) = 0 \]

Die beiden Ortsvektoren haben als Komponenten die Koordinaten der Punkte, auf welche sie zeigen, d.h. für den Punkt \(A\):

\[ \overrightarrow{OA}=\begin{pmatrix} A_x \\ A_y \end{pmatrix} \]

Das Gleiche machen wir für den Punkt \(P\), allerdings wählen wir eine leicht andere Schreibweise:

\[ \overrightarrow{OP}=\begin{pmatrix} x \\ y \end{pmatrix} \]

Der Grund ist der: Der Punkt \(A\) ist fix auf der Geraden und ist unser Stützpunkt. Dieser gibt uns den Anfang vom Ursprung aus. Der Punkt \(P\) steht stellvertretend für alle Punkte auf der Geraden. Die Gerade ist ja eine Punktschar mit unendlich vielen Punkten. Das sind alles \(P\)-Punkte. Wir setzen deshalb die ganz allgemeine Variable \(x\) für die \(x\)-Koordinate auf der Geraden und \(y\) für die \(y\)-Koordinate.

Jetzt schreiben wir die Vektorgleichung in Komponentenschreibweise nochmals hin:

\[ \begin{pmatrix} n_x \\ n_y \end{pmatrix} \cdot \Big( \begin{pmatrix} x \\ y \end{pmatrix} – \begin{pmatrix} A_x \\ A_y \end{pmatrix}\Big) = 0 \]

Wir führen das Skalarprodukt aus, indem wir das Produkt der beiden \(x-\)Komponenten bilden, dann das Produkt der beiden \(y-\)Komponenten dazu addieren und schliesslich das Produkt der beiden \(z-\)Komponenten addieren. Die Summe der drei Produkt muss null ergeben:

\[ n_x \cdot (x – A_x) + n_y \cdot (y – A_y) = 0 \]

Beachte, dass die Normalform in drei Dimensionen eine Ebene und nicht eine Gerade beschreiben würde. Senkrecht zu einem Normalvektor ist in drei Dimensionen ja eine ganze Ebene. Erst durch das Einschränken auf die zweidimensionale \(x,y-\)Ebene, d.h. mit der Forderung \(z=0\), kriegen wir die Gerade, die eigentlich durch den Schnitt der zu \(\vec{n}\) senkrechten Ebene mit der \(z=0\)-Ebene entsteht.

Beispiel

Finde die Normalform der folgenden Geraden \(g\):

---

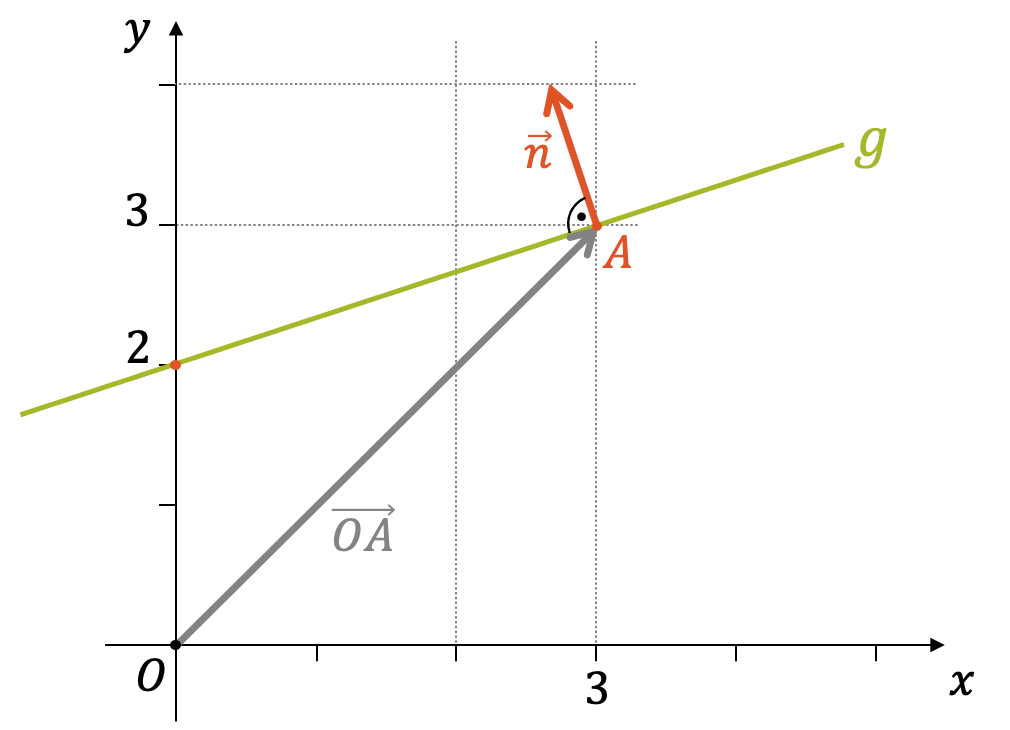
Aus der Grafik entnehmen wir den Stützvektor \(\overrightarrow{OA}\) und den Normalvektor \(\vec{n}\), womit wir die Komponenten \(n_x\), \(n_y\), \(A_x\) und \(A_y\) erhalten:

\[ \overrightarrow{OA} = \begin{pmatrix} 3 \\ 3 \end{pmatrix}, \quad \vec{n} = \begin{pmatrix} -\frac{1}{3} \\ 1 \end{pmatrix} \]

\[ n_x = -\frac{1}{3}, \;\; n_y = 1, \]

\[ A_x = 3, \;\; A_y = 3 \]

Das setzen wir jetzt in die allgemeine Normalform ein und erhalten die folgende Gleichung:

\[ \underline{g: \quad -\frac{1}{3} \cdot (x – 3) + 1 \cdot (y – 3) = 0} \]

Wenn wir die Gleichung noch etwas ausmultiplizieren und aufräumen, erhalten wir die folgende Gleichung:

\[ g: \quad -\frac{1}{3} x + y – 2 = 0 \]

Das ist die sog. Koordinatenform, die wir v.a. für Ebenen gebrauchen werden, weniger für Geraden. Wir können diese Gleichung auch nach \(y\) auflösen und erhalten die allgemeine Form einer Geraden:

\[ y = \frac{1}{3} x + 2 \]

Hier erkennen wir die Funktionsgleichung einer linearen Funktion mit Steigung \(\frac{1}{3}\) und Achsabschnitt \(+2\).