Punkt und Gerade

Punkt auf der Geraden

Liegt ein Punkt auf einer Geraden oder nicht? Nun, das können wir relativ einfach beantworten. Eine Geradengleichung hat ja die folgende Struktur: “Ein Punkt \(A\) auf der Geraden plus ein Vielfaches (\(\lambda\)) eines Vektors (\(\overrightarrow{AB}\)), der die Richtung der Geraden vorgibt, ergibt einen weiteren Punkt \(P\) auf dieser Geraden. Je nach Faktor erhalten wir einen anderen Punkt \(P\). Das gibt schliesslich alle Punkte auf der Geraden.

\[ \overrightarrow{OP} \;\; = \;\; \overrightarrow{OA} + \lambda \cdot \overrightarrow{AB} \]

Wir möchten jetzt wissen, ob ein ganz bestimmter Punkt \(Q\) auf der Geraden liegt, d.h. ob wir den Ortsvektor von \(Q\) mit der Geradengleichung ausdrücken können:

\[ \overrightarrow{OQ} \;\;=\;\; \overrightarrow{OA} + \lambda_0 \cdot \overrightarrow{AB} \]

Beispiel

Untersuche, ob der Punkt \(Q(1,1,1)\) auf der Geraden \(g\) liegt:

\[ g \colon \;\; \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ -3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -6 \\ 8 \end{pmatrix} \]

---

Der Punkt \(Q\) hat den Ortsvektor \(\overrightarrow{OQ}\):

\[ \overrightarrow{OQ} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \]

Können wir diesen Punkt mit Hilfe der Geradengleichung erreichen, d.h. können wir von \(A\) aus mit dem Vektor \(\overrightarrow{AB}\) auf der Geraden \(g\) so bewegen, dass wir genau \(Q\) erreichen? Die Geradengleichung beschreibt ja, wie jeder Punkt \(P\) auf der Geraden erreicht werden kann. Sie hat die folgende Struktur:

\[ \overrightarrow{OP} = \overrightarrow{OA} + \lambda \cdot \overrightarrow{AB} \]

Wenn ja, dann gibt es einen ganz bestimmten Wert für \(\lambda\), den wir jetzt mal \(\lambda_0\) nennen und der die Verbindung von \(A\) zu \(Q\) herstellt:

\[ \overrightarrow{OQ} = \overrightarrow{OA} + \lambda_0 \cdot \overrightarrow{AB} \]

In Komponentenschreibweise:

\[ \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \;\; \stackrel{!}{=} \;\; \begin{pmatrix} 2 \\ 4 \\ -3 \end{pmatrix} + \lambda_0 \cdot \begin{pmatrix} -2 \\ -6 \\ 8 \end{pmatrix} \]

Diese Vektorgleichung ist eigentlich nichts anderes als ein Gleichungssystem mit drei Gleichungen:

\[ \begin{cases} \begin{array}{cc} 1 \;\; = \;\; 2 + \lambda_0 \cdot (-2) \\ 1 \;\; = \;\; 4 + \lambda_0 \cdot (-6) \\ 1 \;\; = \;\; -3 + \lambda_0 \cdot 8 \end{array} \end{cases} \]

Da wir für nur eine Unbekannte und ganze drei Gleichungen haben, ist das System zweifach überbestimmt, d.h. wir haben mehr Gleichungen als nötig. Was heisst das? Die drei Gleichungen können sich in der Lösung für \(\lambda_0\) einig sein oder nicht. Wenn alle Gleichungen für das gleiche \(\lambda_0\) erfüllt sind, dann haben wir die Lösung gefunden. Wenn es aber kein \(\lambda_0\) gibt, das alle Gleichungen gleichzeitig erfüllt, dann liegt der Punkt nicht auf der Geraden und es gibt keine Lösung.

Wir nehmen z.B. die erste Gleichung und lösen nach \(\lambda_0\) auf:

\[ 1 = 2 + \lambda_0 \cdot (-2) \]

\[ \rightarrow \quad \underline{\lambda_0 = \frac{1}{2}} \]

Jetzt schauen wir, ob die anderen zwei Gleichungen erfüllt sind:

\[ 1 \stackrel{?}{=} 4 + \frac{1}{2} \cdot (-6) \]

\[ 1 \stackrel{?}{=} -3 + \frac{1}{2} \cdot 8 \]

Beide sind erfüllt und damit ist nachgewiesen, dass der Punkt \(Q(1,1,1)\) auf der Geraden liegt, denn er kann mit dem Faktor \(\lambda_0=\frac{1}{2}\) erreicht werden.

Abstand zwischen Punkt und Gerade

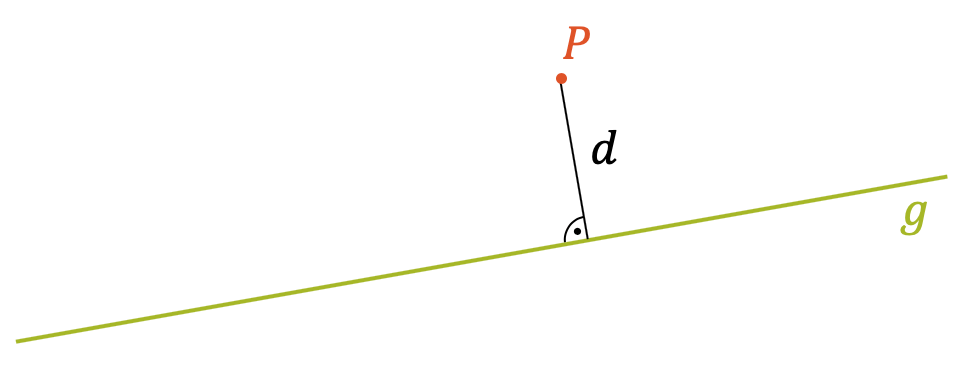
Angenommen wir haben eine Gerade \(g\), die an einem Punkt \(P\) vorbeiführt. Wie gross ist der Abstand \(d\) zwischen der Gerade \(g\) und \(P\)? Dazu brauchen wir natürlich das Lot auf die Gerade, denn das ist die kürzeste Verbindung vom Punkt zur Gerade.

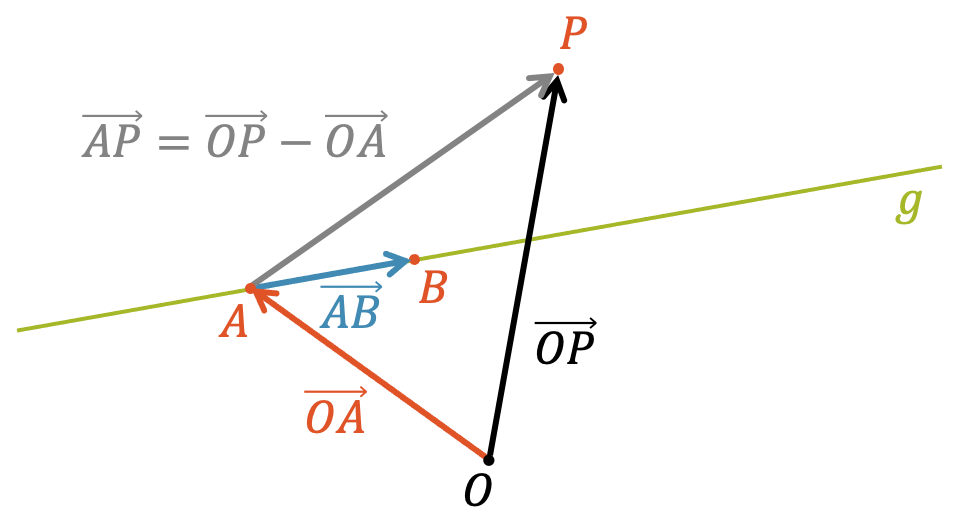
Zuerst wählen wir einen Punkt \(A\) auf \(g\) und bilden eine Vektordifferenz zwischen dem Ortsvektor \(\overrightarrow{OA}\) zum Punkt \(A\) und dem Ortsvektor \(\overrightarrow{OP}\) zum Punkt \(P\), von welchem aus wir den Abstand zu \(g\) herausfinden möchten. Diese Vektordifferenz entspricht dem grauen Vektor von \(A\) nach \(P\) in der nachfolgenden Zeichnung:

\[ \overrightarrow{AP} = \overrightarrow{OP} – \overrightarrow{OA} \]

Mit Hilfe der Vektorgeometrie können wir jetzt ein Vektorprodukt aufstellen, dessen Betrag der Fläche eines Parallelogramms entspricht. Das (orangene) Parallelgramm der Vektoren \(\overrightarrow{AP}\) und \(\overrightarrow{AB}\) hat die gleiche Fläche, wie das (rote) Rechteck mit Grundseite \(\overrightarrow{AP}\) und Höhe \(d\).

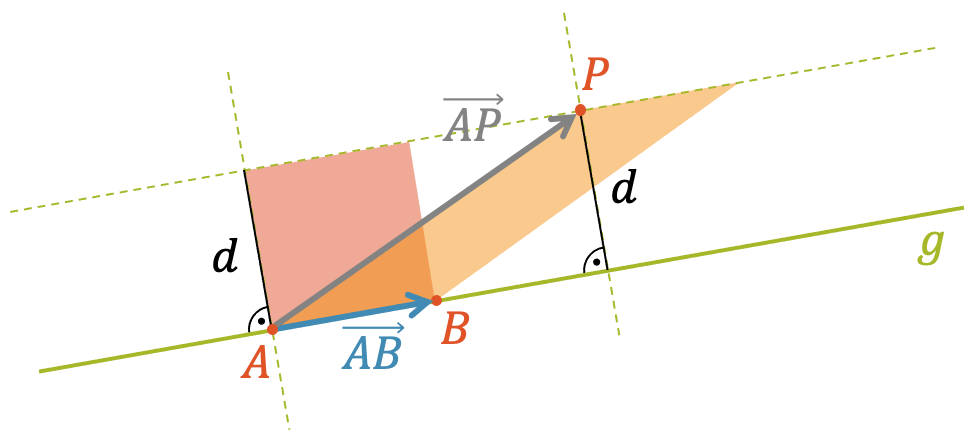
Gemäss dem Prinzip von Cavalieri hat das orangene Parallelogramm die gleiche Fläche \(F\), wie das rote Rechteck:

\[ F = \Big |\overrightarrow{AB} \times \overrightarrow{AP} \Big| = d \cdot |\overrightarrow{AB}| \]

\(F\) können wir mit dem Vektorprodukt berechnen. Da sie auch dem Produkt von Grundseite mit der Länge \(\overrightarrow{AB}\) und der Höhe \(d\) entspricht, können wir sie nach der gesuchten Grösse \(d\) auflösen:

\[ d = \frac{\Big |\overrightarrow{AB} \times \overrightarrow{AP} \Big|}{|\overrightarrow{AB}|} \]

Da wir hier die ganze Sache mit allgemeinen Vektoren beschrieben haben, gilt das auch im Raum für dreidimensionale Vektoren. Das ist dann schon sehr stark, wenn wir den Abstand zu einer Geraden im Raum berechnen können und die Mathematik uns automatisch das Lot auf die Gerade findet.

Beispiel

Zeige, dass die Gerade \(g\) im Abstand von \(d=5\) am Ursprung vorbeiführt.

\[ g: \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 5 \\ 3 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} \]

---

Für den Vektor, der auf der Geraden \(g\) liegt, wählen wir aus der Geradengleichung den Vektor \(\overrightarrow{AB} = \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix}\) und für den Punkt \(A\) die Koordinaten \(A(5,3,1)\), ebenfalls aus der Geradengleichung. Der Ursprung ist der Punkt \(P\) mit den Koordinaten \(P(0,0,0)\). Damit gilt für den Vektor \(\overrightarrow{AP}\):

\[ \overrightarrow{AP} = \overrightarrow{OP} – \overrightarrow{OA} \]

\[ = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} – \begin{pmatrix} 5 \\ 3 \\ 1 \end{pmatrix} = \begin{pmatrix} -5 \\ -3 \\ -1 \end{pmatrix} \]

Jetzt können wir das Vektorprodukt berechnen:

\[ \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} \times \begin{pmatrix} -5 \\ -3 \\ -1 \end{pmatrix} = \begin{pmatrix} 0 \\ -5 \\ 15 \end{pmatrix} \]

Der Betrag davon ist:

\[ \Big| \overrightarrow{AB} \times \overrightarrow{AP} \Big| \]

\[ = \sqrt{0^2 + (-5)^2 + 15^2} \]

\[ = \sqrt{250} = 5 \sqrt{10} \]

Dann berechnen wir noch den Betrag von \(\overrightarrow{AB}\):

\[ \Big| \overrightarrow{AB} \Big| = \sqrt{0^2 + 3^2 + 1^2} \]

\[ = \sqrt{10} \]

So dass wir für den Abstand \(d\) erhalten:

\[ d = \frac{\Big |\overrightarrow{AB} \times \overrightarrow{AP} \Big|}{\big|\overrightarrow{AB}\big|} \]

\[ \require{cancel} = \frac{5 \cancel{\sqrt{10}}}{\cancel{\sqrt{10}}} = \underline{5} \]

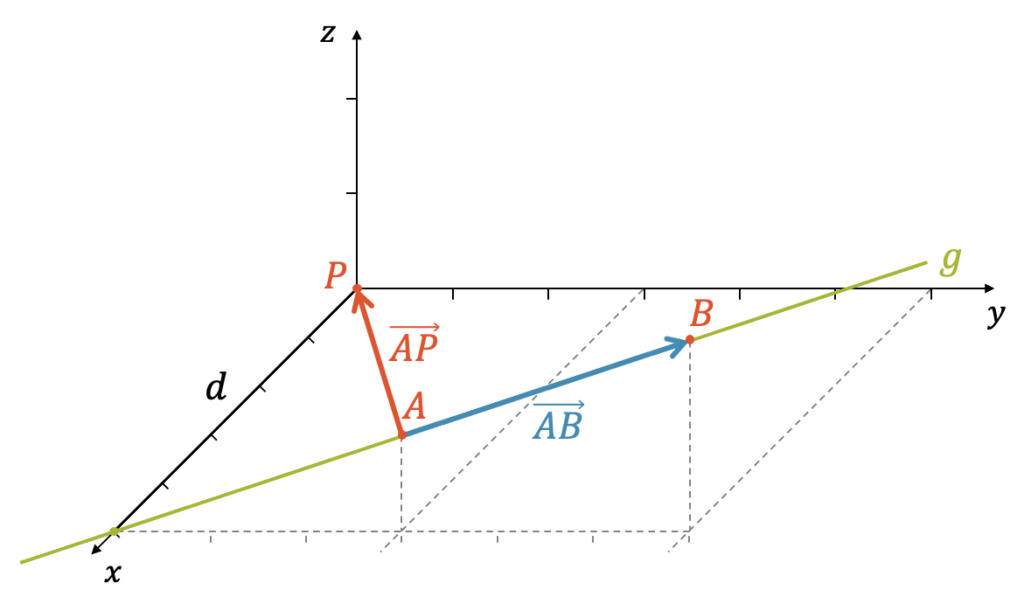
Tatsächlich schneidet die Gerade \(g\) die \(x\)-Achse im Punkt \((5,0,0)\). Da sie in einer Ebene verläuft, die parallel ist zur \(y,z\)-Ebene, ist das Lot von \(P\) auf \(g\) gerade in der \(x\)-Achse und somit beträgt \(d=5\).