Das Wichtigste in Kürze
Ein Stapel von Flächen kann beliebig verschoben werden, ohne dass die Anzahl Flächen sich verändert hat. Damit haben die verschiedenen verschobenen Varianten jeweils das gleiche Volumen.
Das Gleiche gilt im zweidimensionalen Fall für einen Stapel von Linien, die zusammen eine Fläche bilden. Diese Fläche bleibt gleich, unabhängig davon, wie verschoben der Stapel ist.
Hack
Wenn Du eine Fläche oder ein Volumen von etwas “schrägem” berechnen musst, erinnere dich daran, dass einzig die Grundfläche/Grundlinie und die Höhe ausschlaggebend sind. Der Stapel kann ja beliebig verschoben sein.
Meist gibt es den einfachen rechtwinkligen oder geraden Fall (Fläche eines Rechtecks, Volumen eines Quaders etc.). Berechne diesen einfachen Fall und übertrage dein Resultat auf den schrägen Fall mit dem Prinzip von Cavalieri.
Video
Du kannst dich leicht davon überzeugen, dass ein gerades und ein gleich hohes, aber schräges Prisma das gleiche Volumen haben, wenn du dir vorstellst, ein Prisma mit einem Stapel Notizzettel “gebaut” zu haben. Alle Notizzettel haben z.B. die gleiche quadratische Grundfläche. Bei quadratischen Zetteln entsteht mit einem geraden Stapel ein Quader, dessen Volumen einfach Grundfläche \(G\) mal Höhe \(h\) ist:
\[ V = G \cdot h \]
Wir können den gleichen Stapel aber auch anschrägen. Da die Anzahl Zettel gleich ist, muss die Menge an Papier und damit das Volumen auch gleich geblieben sein.
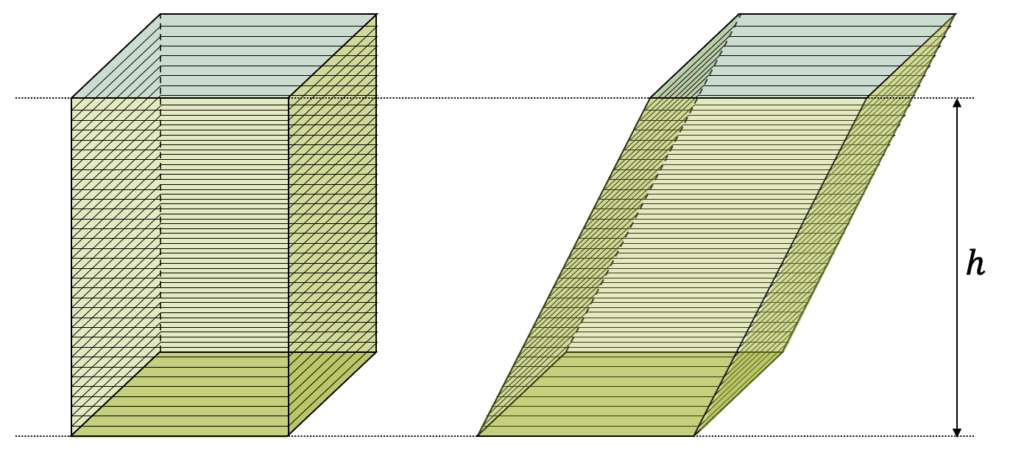
Das schräge Prisma hat deshalb das gleiche Volumen wie das gerade Prisma, solange wir die gleiche Höhe und die gleichen Zettel (gleiche Grundfläche) verwenden.
Bonaventura Cavalieri (1598 – 1647) war ein italienischer Mathematiker und Astronom. Nach ihm ist dieses Prinzip benannt.
“Mit seinem Prinzip legte Cavalieri sogar das Fundament für die Integralrechnung, die später folgen sollte”
Bis hierhin haben wir immer die gleichen “Zettel” oder Grundflächen benutzt. Das muss aber nicht sein, wie wir im Beispiel des Dreiecks oder der Pyramide gleich erkennen werden.
Ein Dreieck mit Grundseite \(s\) kann als Stapel von Linien betrachtet werden.
Diesen Stapel können wir beliebig hin und herschieben. Was sich nicht ändert sind die Art und Anzahl der Linien. Wir schieben sie nur ein bisschen nach links oder rechts.
Die verschieden farbigen Dreiecke haben somit immer die gleiche Grundseite \(s\) und gleiche Höhe \(h\) und damit die gleiche Fläche \(A\).
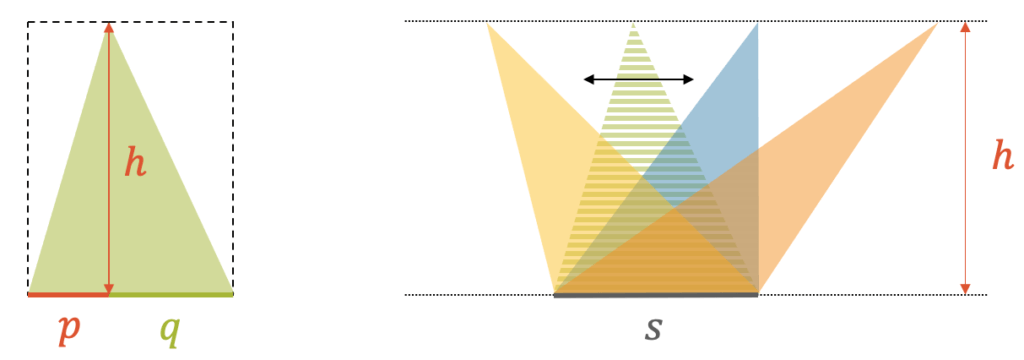
Ein Dreieck ist dabei besonders einfach zu berechnen. Es ist das blaue rechtwinklige Dreieck (rechts). Seine Fläche entspricht genau der Hälfte eines Rechtecks mit Grundseite \(s\) und Höhe \(h\).
\[ A = \frac{1}{2} \cdot s \cdot h \]
Wir können die Fläche auch erkennen als Summe von zwei halben Rechtecken (siehe links)
\[ A_1 = \frac{1}{2} \cdot p \cdot h\]
\[ A_2 = \frac{1}{2} \cdot q \cdot h\]
Das Dreieck hat also die Fläche \(A=A_1+A_2\) und somit:
\[ A = \big( \frac{1}{2} \cdot p \cdot h \big) + \big( \frac{1}{2} \cdot q \cdot h \big) = \frac{1}{2} \cdot (p + q) \cdot h = \frac{1}{2} \cdot s \cdot h \]
Die Fläche des Dreiecks ist nur abhängig von der Grundfläche \(s=(p+q)\) und der Höhe \(h\), nicht aber vom Winkel!
Aufgabensammlung
Lernziele
- Du kannst das Prinzip von Cavalieri in eigenen Worten ausdrücken und Beispiele dazu machen, sowohl in 2D (Fläche), wie auch in 3D (Volumen)
Weitere Links
Bonaventura Cavalieri (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.