Prismen

Volumen

Ein Prisma entsteht, wenn ein regelmässiges oder unregelmässiges Vieleck im Raum parallelverschoben wird. Die Grundseite und die Oberseite sind zwei identische Vielecke in zwei parallelen Ebenen. Die Seitenflächen sind Rechtecke oder Parallelogramme, je nachdem ob die Parallelverschiebung senkrecht zur Grundseite oder schräg dazu statt gefunden hat. Im den zwei folgenden Beispielen wurden zwei regelmässige Sechsecke parallelverschoben, einmal zu einem geraden Prisma (links) und dann zu einem schrägen Prisma (rechts).

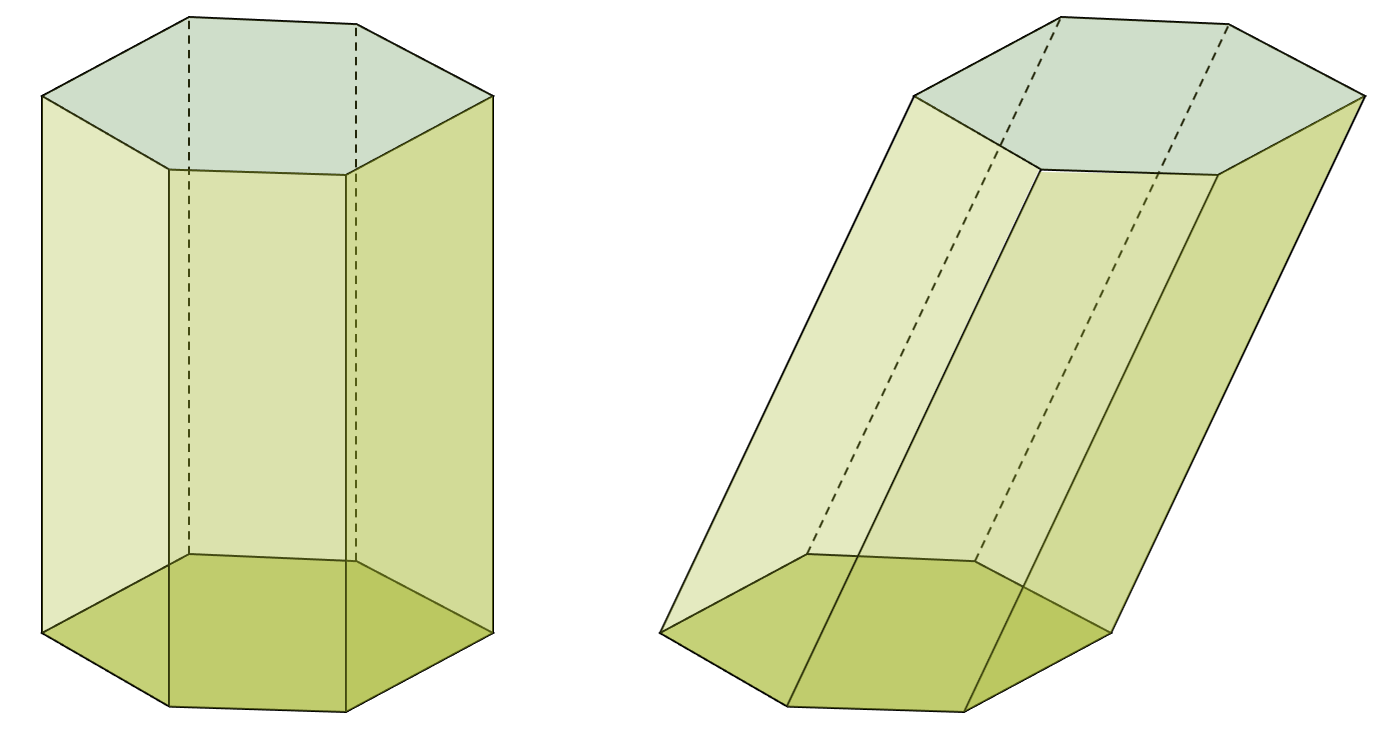
Interessanterweise haben die beiden obigen Prismen das genau gleiche Volumen, da dieses nur von der Grundfläche und der Höhe des Prisma abhängt, nicht aber vom Umstand, ob das Prisma gerade oder schräg ist.

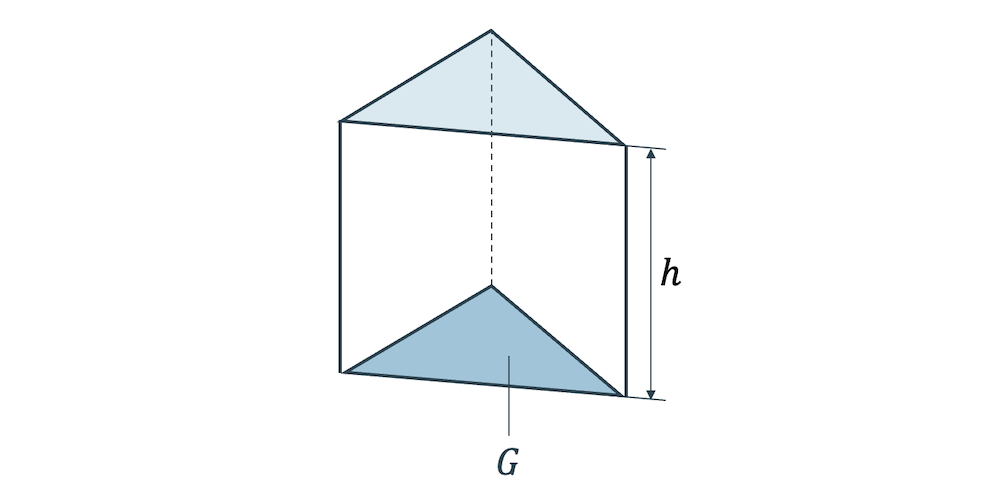
Das Volumen eines Prismas entspricht der Grundfläche \(G\) mal der Höhe \(h\), unabhängig vom Winkel, den die Seitenflächen zur Grundfläche haben:

\[ V = G \cdot h \]

Oberfläche

Die Oberfläche \(O\) eines Prismas besteht aus der Grund- und Oberseite und den Mantelflächen. Die Mantelflächen sind Rechtecke und Parallelogramme. Für die Fläche eines Parallelogramms können wir wieder das Prinzip von Cavalieri anwenden, denn sie sind nichts anderes als schiefe Stapel von gleich langen Grundseiten, d.h. deren Fläche ist gleich derjenigen des ursprünglichen Rechtecks.

Die Oberfläche \(O\) eines Prismas besteht aus der Grund- und Oberseite und den Mantelflächen, die Rechtecke oder Parallelogramme sind. Für Parallelogramme gilt wieder das Prinzip von Cavalieri, d.h. deren Fläche ist gleich der Grundseite mal die Höhe, unabhängig vom Winkel.

Beispiel

Berechne das Volumen \(V\) und die Oberfläche \(A\) des Prismas, das durch zwei gleichseitige Dreiecke (Seitenlänge \(s\)) und drei quadratische Seitenflächen gebildet wird.

Lösung

Zuerst berechnen wir die Grundfläche \(G\), d.h. die Fläche des gleichseitigen Dreiecks mit Seitenlänge \(s\): \[ G = \frac{1}{2} \cdot s \cdot \frac{\sqrt{3}}{2} s = \frac{\sqrt{3}}{4} s^2 \] Jetzt können wir die Grundfläche mit der Höhe des Prismas multiplizieren. Da die Seitenflächen quadratisch sind, beträgt die Höhe ebenfalls \(s\): \[ V = G \cdot h = \frac{\sqrt{3}}{4} s^2 \cdot s = \underline{\frac{\sqrt{3}}{4} s^3} \] Für die Oberfläche \(O\) des Prismas müssen wir die zwei Grundflächen und die drei Quadratsflächen addieren: \[ O = 2G + 3s^2 = 2 \cdot \frac{\sqrt{3}}{4} s^2 + 3s^2 = \underline{\Big(\frac{\sqrt{3}}{2}+3\Big)\cdot s^2} \]

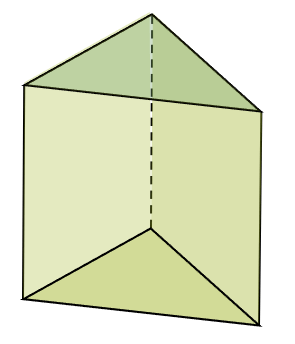
Netz

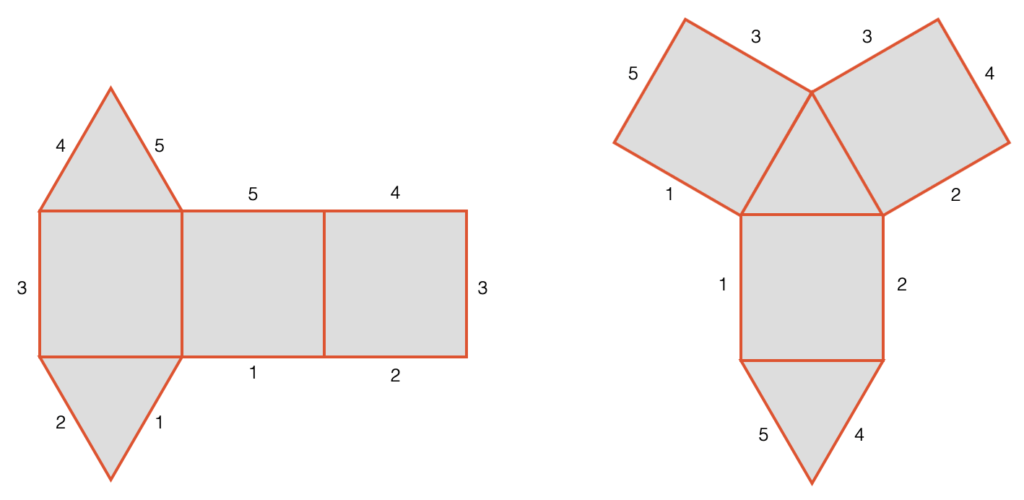
Für geometrische Körper kann in der Regel ein sog. Netz (oder auch Körpernetz) konstruiert werden. Es ist gewissermassen die “Bastelanleitung”, um den Körper aus Papier oder Karton zu bauen. Die Seitenflächen werden über gemeinsame Kanten verbunden. Viele Kanten sind aber getrennt gezeichnet und werden erst beim Bauen des Körpers zusammengefügt. Die Zusammengehörigkeit von Kanten kann mit Hilfe von kleine Ziffern angedeutet werden.

Beispiel

Zeichne ein mögliches Netz für das Prisma mit quadratischen Seitenflächen und nummeriere die Kanten, die zusammengehören.

Lösung

Nachfolgend sind zwei mögliche Varianten gezeichnet. In jedem Fall müssen natürlich die fünf Seitenflächen vorhanden und deren gemeinsame Kanten gleich lang sein.