Kegel

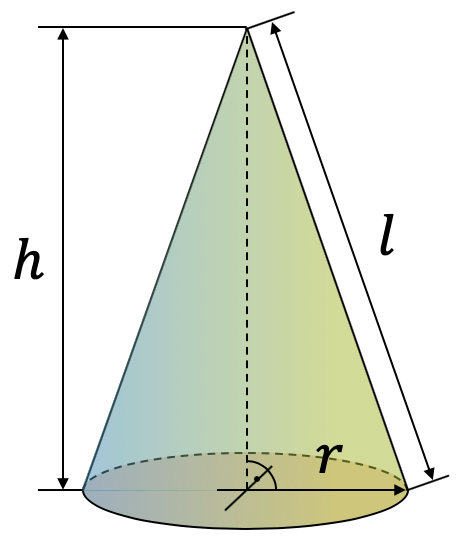
Genauso wie wir aus dem Prisma einen Zylinder gemacht haben, können wir aus einer Pyramide einen Kegel machen. Die Grundfläche ist ein Kreis, d.h. näherungsweise ein \(n\)-Eck mit einer extrem grossen Zahl Ecken bzw. \(n \rightarrow \infty\). Wenn der Kegel also eine Pyramide mit einem \(n\)-Eck als Grundfläche ist (\(n \rightarrow \infty\)), dann können wir das Kegelvolumen einfach berechnen als das Drittel des Produkts einer Kreisfläche mal die Höhe:

\[ V = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} \cdot \pi r^2 \cdot h \]

Für die Kegeloberfläche müssen wir die Grundfläche und die Mantelfläche addieren. Die Grundfläche ist eine Kreisfläche, die wir kennen. Für die Mantelfläche müssen wir uns zuerst überlegen, um welche Art von Fläche es sich handelt. Wir wissen, dass sie in einem Punkt endet, denn der Kegel hat, wie die Pyramide, eine Spitze. Die untere Kante ist ein Kreisbogen. Die Kombination von einem Punkt und einem Kreisbogen ergibt einen Kreissektor, was der geometrische Begriff für ein “Kuchenstück” ist, wobei der Winkel beliebig gross oder klein sein kann.

Der Kreisbogen hat die gleiche Länge wie der ganze Umfang \(U = 2 \pi r\) der Grundfläche, da es ja die gemeinsame Kante ist. Der Kreisbogen hat aber einen anderen Radius, nämlich die Länge der sog. Mantellinie \(l\). Wir schauen uns dazu einen seitlichen Schnitt durch den Kegel an und kriegen dann die Mantellinie als Kante des Schnitts mit Hilfe des Satzes von Pythagoras:

\[ l^2 = h^2 + r^2 \]

Wir haben jetzt den Radius unseres Kreissektors. Wie steht es jetzt aber mit seinem sog. Mittelpunktswinkel \(\varphi\)? Dazu nehmen wir die Bedingung, dass der Bogen \(b\) des Kreissektors genau gleich lang sein muss, wie der Kreisumfang der Grundfläche. Der Kreisbogen \(b\) ist gleich einem Bruchteil des ganznen Kreises mit Radius \(l\). Wir multiplizieren deshalb den Umfang des grossen Kreises (mit Radius \(l\)) mit dem Bruchteil von \(\varphi\) als Teil des ganzen Kreises (360° bzw. \(2\pi\)).

\[ b = \frac{\varphi}{2 \pi} \cdot 2 \pi l \quad \stackrel{!}{=} \quad 2 \pi r = U \]

Für den Winkel des Kreissektors \(\varphi\) (in Bogenmass) erhalten wir damit:

\[ \varphi = \frac{2 \pi r}{l} \]

In unserem Beispiel ist die Seitenkante \(l\) rund drei mal länger als der Kreisradius der Grundfläche, d.h. \(\varphi\) ist rund ein Drittel eines ganzen Kreises oder ca. 120°. Damit wird der Kreisbogen \(b\) gleich lang wie der Kreis mit Umfang \(U\). Wir können jetzt das Netz des Kegels zeichnen:

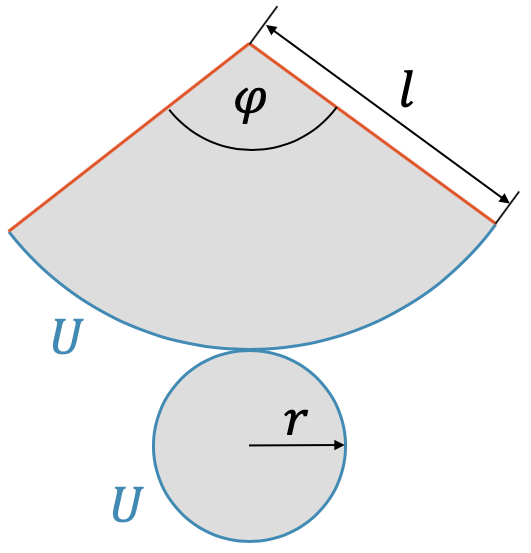
Die Mantelfläche \(A_M\) ist ebenfalls der \(\varphi\)-Bruchteil der Fläche des grossen Kreises:

\[ A_M = \frac{\varphi}{2 \pi} \cdot \pi l^2 =  \varphi \cdot \frac{1}{2 \pi} \cdot \pi l^2 \]

Nun setzen wir den oben gefundenen Ausdruck für \(\varphi\) ein:

\[ \require{cancel} A_M = \frac{\cancel{2 \pi} r}{\cancel{l}} \cdot \frac{1}{\cancel{2 \pi}} \cdot \pi l^{\cancel{2}} = \pi r l \]

Für die Oberfläche \(O\) des Kegels erhalten wir somit:

\[ O = G + A_M = \pi r^2 + \pi r l = \pi r \cdot (r+l) \]

Beispiel

Berechne das Volumen und die Oberfläche des folgenden Kegelstumpfs.

---

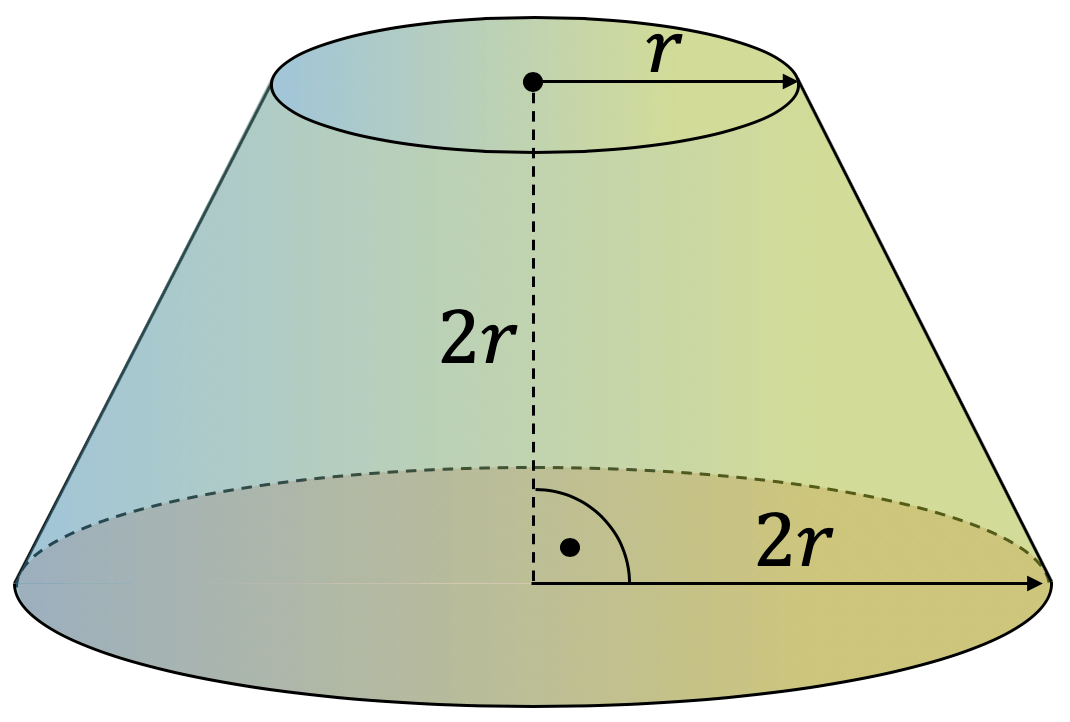
Für das Volumen erkennen wir, dass der Kegelstumpf eigentlich ein ursprünglich grosser Kegel war, dem der obere Teil (ebenfalls ein Kegel) weggeschnitten worden ist. Wir können deshalb das Volumen des Kegelstumpfs als Differenz von einem ursprünglich grossen Kegel \(V_1\) und dem weggeschnittenen kleinen Kegel mit Volumen \(V_2\) betrachten:

\[ V = V_1 – V_2\] 

Der ursprüngliche Kegel hatte die gleiche Grundfläche wie der Kegelstumpf, d.h. \(G_1=\pi \cdot (2r)^2\). Mit Hilfe des Strahlensatzes erkennen wir, dass die ursprüngliche Höhe des Kegels \(4r\) war. Die Mantellinie begrenzt den Radius auf \(2r\) auf der Höhe der Grundfläche. Mit einer Höhe von \(2r\) nimmt der Radius um die Hälfte ab, d.h. mit einer gedanklichen Verlängerung der Mantellinie um weitere \(2r\) sind wir an der Kegelspitze angelangt. Mit Grundfläche \(G_1\) und Höhe \(h_1\) können wir jetzt das Volumen des ursprünglich grossen Kegels berechnen:

\[ V_1 = \frac{1}{3} \cdot G_1 \cdot h_1 = \frac{1}{3} \cdot \pi (2r)^2 \cdot 4r = \frac{16}{3} \pi r^3 \]

Die weggeschnittene Kegelspitze hat eine Grundfläche \(G_2=\pi r^2\) und eine Höhe \(h_2=2r\):

\[ V_2 = \frac{1}{3} \cdot G_2 \cdot h_2 = \frac{1}{3} \cdot \pi r^2 \cdot 2r = \frac{2}{3} \pi r^3 \]

So erhalten wir das Volumen des Kegelstumps:

\[ V = V_1 – V_2 = \frac{16}{3} \pi r^3 – \frac{2}{3} \pi r^3 = \underline{\frac{14}{3} \pi r^3} \]

Für die Oberfläche berechnen wir zuerst die Mantelfläche, denn der Boden und der Deckel sind einfache Kreisflächen. Für die Mantelfläche \(A_M\) verwenden wir den gleichen Ansatz, nämlich den der Differenz von zwei Kegeln:

\[ A_M = A_{M1} – A_{M2} \]

Für die Mantelfläche wird die Mantellinie benötigt. Wir berechnen Sie mit dem Satz des Pythagoras. Für den grossen ursprünglichen Kegel erhalten wir:

\[ l_1^2 = (4r)^2 + (2r)^2 = 20r^2 \quad \rightarrow \quad l_1 = 2 \sqrt{5}\; r \]

\[ A_{M1} = \pi \cdot (2r) \cdot 2 \sqrt{5}\; r = 4 \sqrt{5}\; \pi \; r^2 \]

Für den kleinen Kegel, der weggeschnitten worden ist, erhalten wir:

\[ l_2^2 = (2r)^2 + r^2 = 5r^2 \quad \rightarrow \quad l_2 = \sqrt{5}\; r \]

\[ A_{M2} = \pi \cdot r \cdot \sqrt{5}\; r = \sqrt{5}\; \pi \; r^2 \]

Wir bilden jetzt die Differenz der beiden Kegelmantelflächen:

\[ A_M = A_{M1} – A_{M2} = 4 \sqrt{5}\; \pi \; r^2 – \sqrt{5}\; \pi \; r^2 = 3 \sqrt{5}\; \pi \; r^2 \]

Jetzt fügen wir noch die beiden Kreisflächen G_1 und G_2 hinzu und erhalten so die gesamte Oberfläche des Kegelstumpfs:

\[ O = G_1 + G_2 + A_M = \pi (2r)^2 + \pi r^2 + 3 \sqrt{5}\; \pi \; r^2 = \underline{(5 + 3 \sqrt{5}) \pi \; r^2} \]