Das Wichtigste in Kürze
Die meisten archimedischen Körper lassen sich aus den platonischen Körpern ableiten, indem ihnen die Ecken (oder Kanten) abgeschnitten werden, so dass regelmässige Seitenflächen entstehen:
-
- Die Seitenflächen des archimedischen Körpers sind zwei oder drei Sorten von regelmässigen Polygonen
-
- Der Körper ist rotationssymmetrisch, d.h. wir können den Körper um einen bestimmten Winkel drehen und der Körper sieht wieder genau gleich aus, wie vor der Rotation
Es gibt total 13 archimedische Körper.
Häufigste Fragen
Archimedes von Syrakus (287 v. Chr. – 212 v. Chr.) war ein griechischer Mathematiker, Physiker und Ingenieur und gilt als einer der bedeutendsten Mathematiker der Antike. Er kannte die platonischen Körper
Archimedes überlegte sich, was mit den platonischen Körpern passieren würde, wenn man ihnen die Ecken abschneiden würde.
Natürlich sollte die hoch stehende Symmetrie weiterhin gewahrt bleiben, d.h. die Ecken würden so abgeschnitten, dass die Kanten alle gleich lang wären.
Die ursprünglichen Seitenflächen würden eine neue aber wieder regelmässige Form erhalten.
Die abgeschnittenen Ecken würden ebenfalls regelmässige Seitenflächen bilden, die jedoch nicht gleich sein müssen, wie die ursprünglichen Seitenflächen.
- Die Seitenflächen des archimedischen Körpers sind regelmässige Polygone
- Der Körper ist rotationssymmetrisch, d.h. wir können den Körper um einen bestimmten Winkel drehen und der Körper sieht wieder genau gleich aus, wie vor der Rotation
Wenn wir beispielsweise beim Hexaeder (Würfel) die acht Ecken abschneiden, entsteht bei den Seitenflächen aus dem Quadrat ein Achteck.
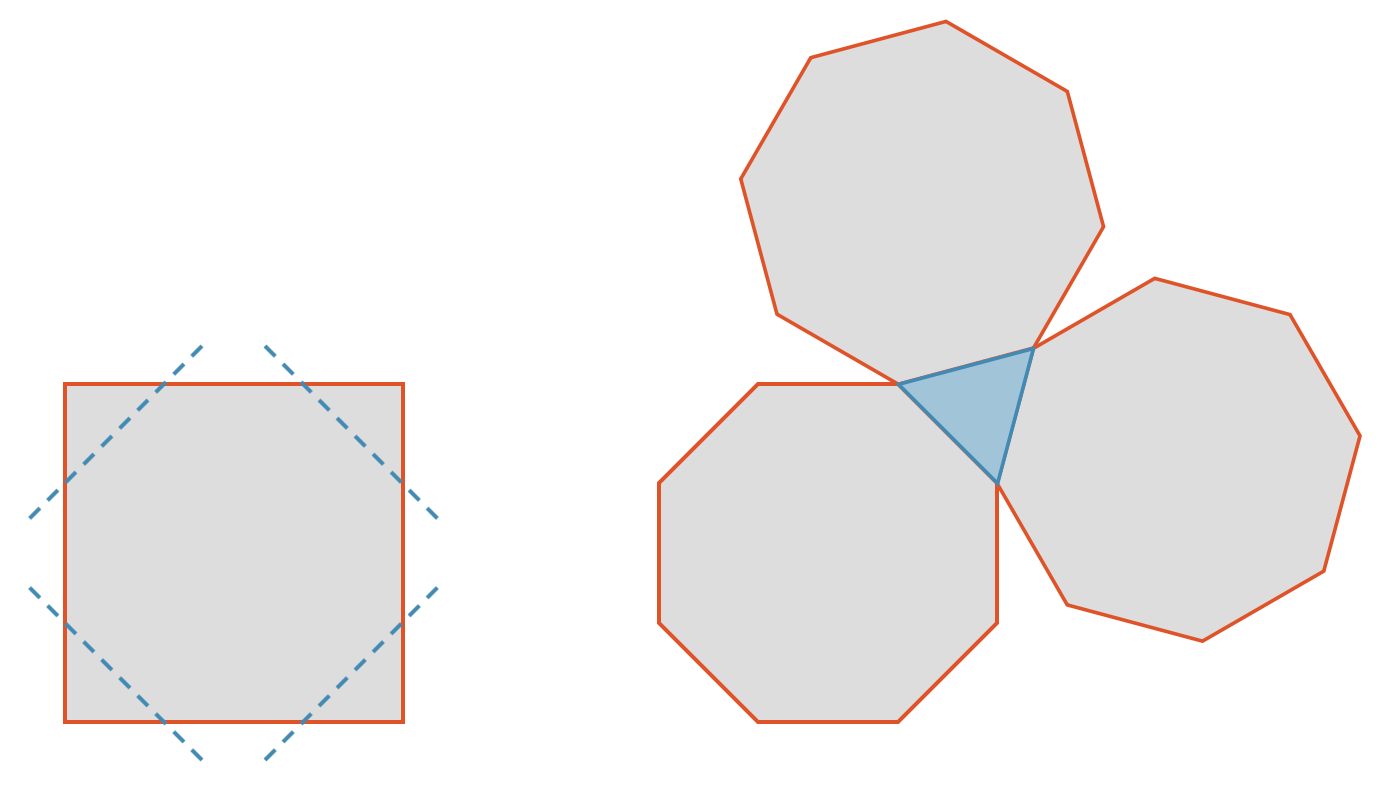
Die Ecken selbst sind gleichseitige Dreiecke. Den Körper, den wir damit erhalten, hat somit:
- 6 Seitenflächen als Achtecke
- 8 Seitenflächen als Dreiecke
Der neue Körper heisst übrigens Hexaederstumpf, weil wir dem Hexaeder die “scharfen” Ecken abgestumpft haben. Er ist ein archimedischer Körper, von denen es, je nach Zählweise, 13 oder 15 Stück gibt.
Beispiel
Wie heisst der archimedische Körper, der aufgrund des Ikosaeders entsteht?
Wie viele Ecken, Kanten und Flächen hat er?
Das Ikosaeder hat 20 gleichseitige Dreiecke als Seitenflächen. Wenn wir die Ecken abschneiden, erhalten wir einen sog. Ikosaederstumpf.
Da an einer Körperecke fünf Dreiecke zusammenstossen, entsteht hier ein neues Fünfeck, wenn wir die Ecke abschneiden.
Dreiecke, die an ihren drei Ecken abgeschnitten werden, werden zu Sechsecken.
Aus den 20 Dreiecken entstehen deshalb 20 Sechsecke und aus den 12 Körperecken entstehen 12 Fünfecke. Wir haben deshalb:
\[ \underline{F = 20 + 12 = 32} \]
Die ursprüngliche Zahl der Ecken von 12 wurde verfünffacht, da jede Ecke zu einem Fünfeck wurde:
\[ \underline{E = 5 \cdot 12 = 60} \]
Die ursprünglichen 30 Kanten sind geblieben und wurden verkürzt. Zu jeder der 12 Ecken sind fünf Kanten hinzugekommen, d.h. wir haben:
\[ \underline{K = 30 + 5 \cdot 12 = 90} \]
Aufgabensammlung
Lernziele
- Du weisst, wie archimedische Körper entstehen und weisst auch, wie mit diesem Wissen die Anzahl Flächen, Kanten und Ecken berechnet werden können.
Weitere Links
Archimedische Körper (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Kommentar oder Frage schreiben
Du musst angemeldet sein, um einen Kommentar abzugeben.