Inhalt
Das Wichtigste in Kürze
Der Euler’sche Polyedersatz gilt für alle konvexen Polyeder, d.h. für jeden dreidimensionalen Körper, der aus vielen Flächen besteht, die durch nach aussen gerichtete Kanten getrennt sind:
\[ E – K + F = 2 \]
Dabei sind:
-
- \(E\) die Anzahl Ecken
- \(K\) die Anzahl Kanten
- \(F\) die Anzahl Flächen
Eulers Polyedersatz geht auf den Schweizer Mathematiker und Physiker Leonhard Euler (1707 – 1783) zurück.
Er gilt für jeden konvexen Polyeder, d.h. für jeden dreidimensionalen Körper, der aus vielen Flächen besteht, die durch nach aussen gerichtete Kanten getrennt sind. Der Polyedersatz besagt:
\[ E – K + F = 2 \]
Dabei sind:
- \(E\) die Anzahl Ecken
- \(K\) die Anzahl Kanten
- \(F\) die Anzahl Flächen
Der Euler’sche Polyedersatz gilt für allgemeine, unregelmässige Polyeder. Natürlich gilt er dann auch für die speziell regelmässigen Polyeder:
Beispiel
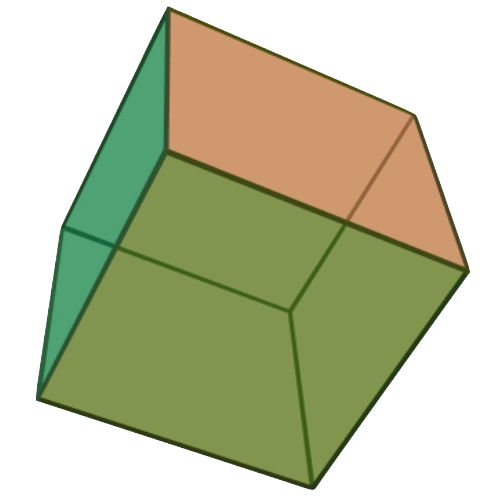
Beispiel
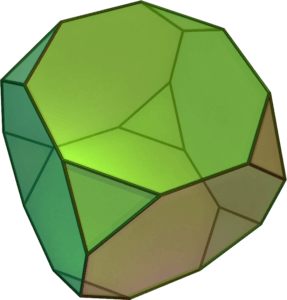
Beispiel
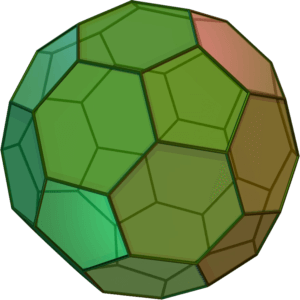
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.