Zentrische Streckung

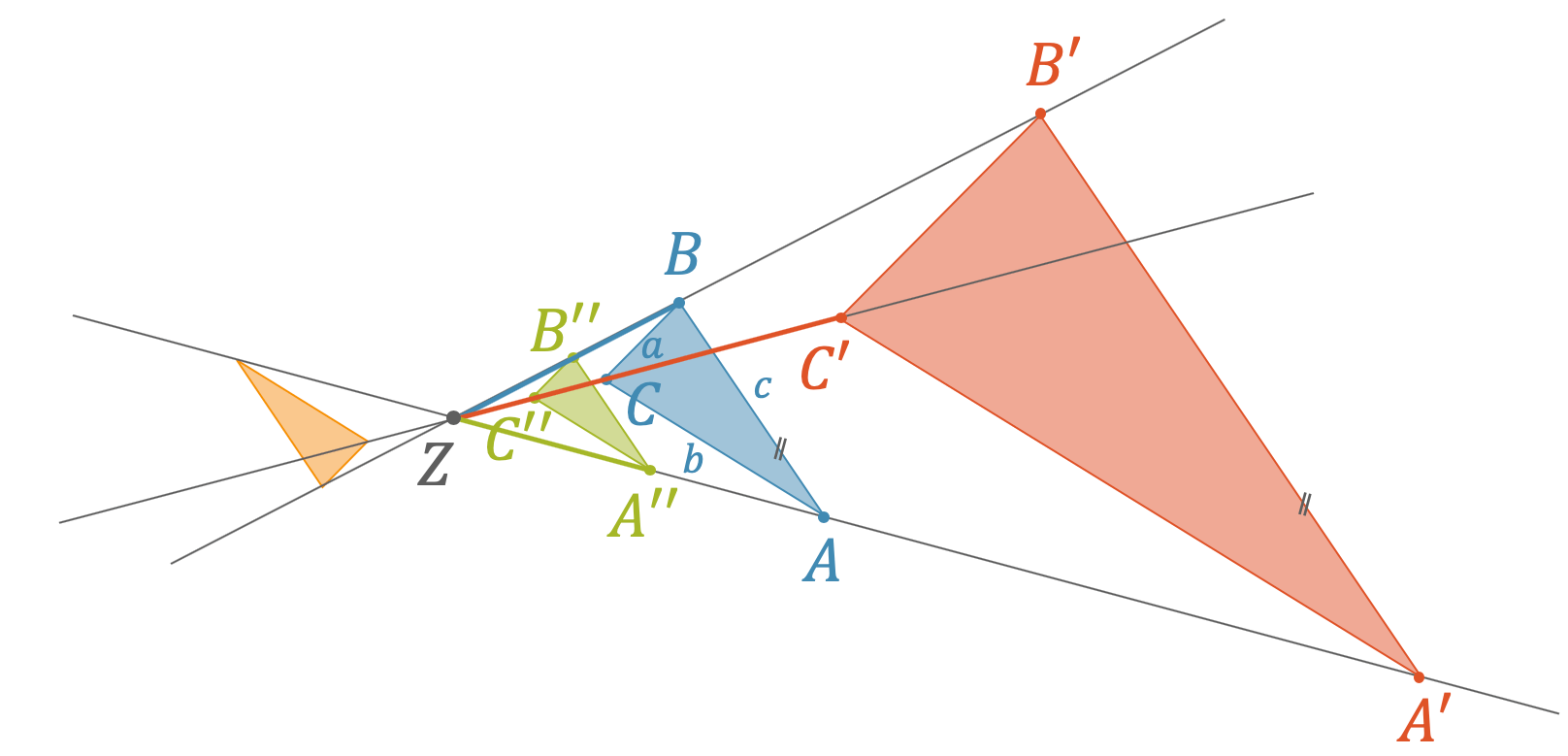
Angenommen wir starten mit einem blauen Dreieck in der obigen Abbildung. Wenn Sie die Strecke \(\overline{ZC}\) mit einem Faktor \(k=2\) multiplizieren, kriegen Sie die neue rote Strecke \(\overline{ZC’}\). Werden die Strecken \(\overline{ZA}\) und \(\overline{ZB}\) mit dem gleichen Faktor \(k\) multipliziert, kriegen Sie entsprechend \(\overline{ZA’}\) und \(\overline{ZB’}\). Auf diese Weise erhalten Sie das neue rote Dreieck \(A’B’C’\).

\[ \overline{ZA’} = k \cdot \overline{ZA}, \qquad \overline{ZB’} = k \cdot \overline{ZB}, \qquad \overline{ZC’} = k \cdot \overline{ZC} \]

Da wir auf jedem Strahl mit dem gleichen Faktor multipliziert haben, gilt die Umkehrung des Ersten Strahlensatzes: Die Seiten \(a, b\) und \(c\) des blauen Dreiecks sind parallel zu den Seiten des neuen roten Dreiecks \(a’, b’\) und \(c’\). Somit sind alle Winkel gleich. Aus dem Zweiten Strahlensatz folgt zudem, dass die Seiten des roten Dreiecks, wie die Strecken auf den Strahlen mit dem Faktor \(k=2\) gestreckt worden sind. Das rote Dreieck ist doppelt so gross wie das blaue Dreieck. Beachten Sie, dass die Fläche des neuen Dreiecks mit dem Faktor \(k^2\) multipliziert worden ist, d.h. die Fläche ist 4-fach.

Was passiert, wenn man mit einem kleinen Faktor multipliziert, z.B. \(k=\frac{1}{2}\) ? Jede Strecke auf dem Strahl wird halbiert und es entsteht ein halb so grosses grünes Dreieck, mit einer Fläche, die \(k^2=\bigl(\frac{1}{2}\bigr)^2\)-mal so gross ist, also 4-fach kleiner ist.

Wenn der Streckungsfaktor negativ \((k<0)\) ist, werden die Strecken auf den Strahlen auf die andere Seite des Zentrums gespiegelt und es entsteht ein punktsymmetrisch gespiegeltes Bild (oranges Dreieck).