Strahlensätze

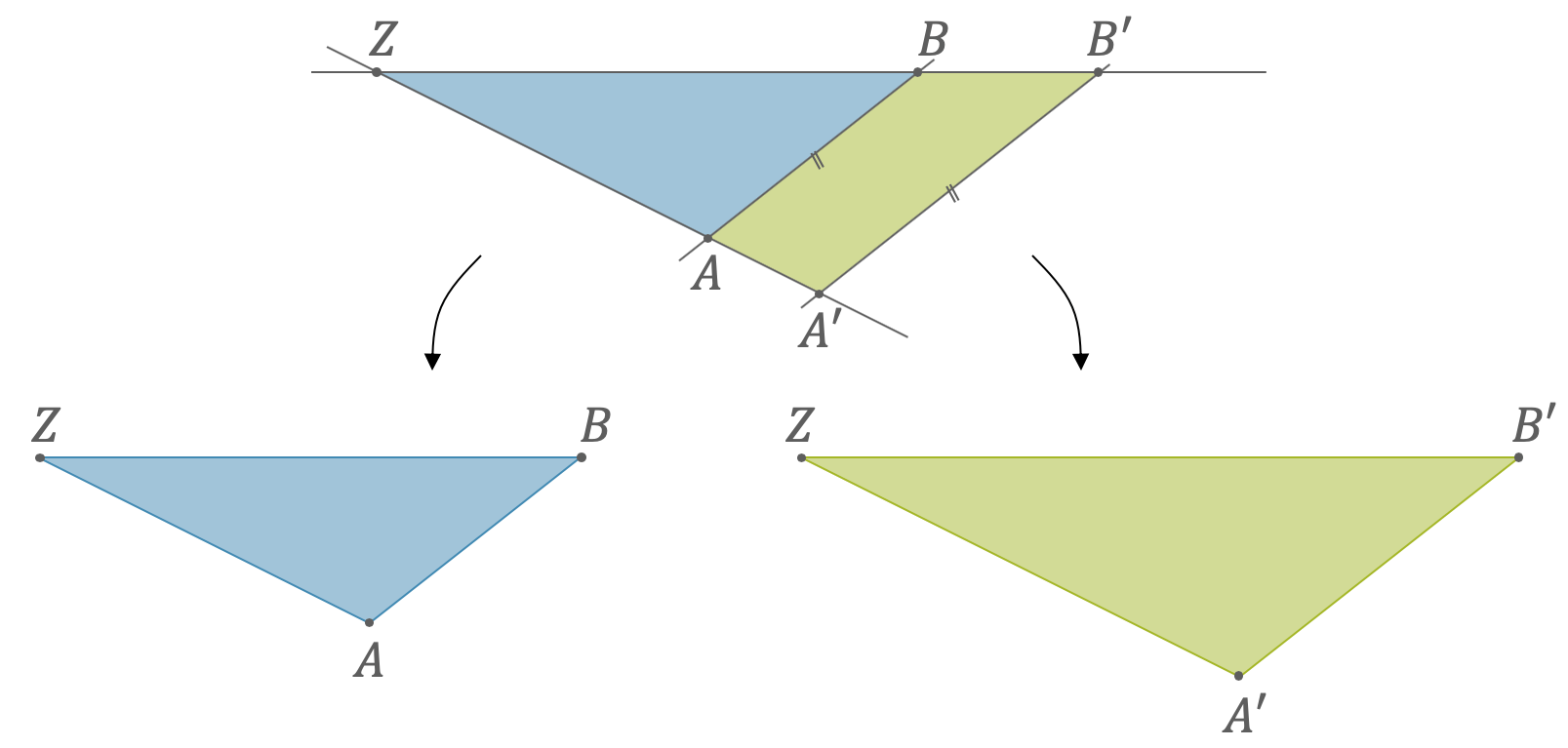
Wenn zwei Strahlen, die vom gleichen Zentrum \(Z\) kommen, von zwei parallelen Geraden geschnitten werden, entstehen zwei Dreiecke \(ZAB\) und \(ZA’B’\). Wir erkennen relativ schnell, dass die beiden Dreiecke die gleichen Winkel haben müssen. Der Winkel bei \(Z\) ist so der so der gleiche Winkel. Der Winkel bei \(A\) muss gleich dem Winkel bei \(A’\) sein, da die beiden Gerade parallel verlaufen und somit diesen Strahl unter dem gleichen Winkel schneiden müssen. Das Gleiche gilt dann auch bei \(B\) und \(B’\).

Wenn wir das blaue Dreieck um 180° drehen und wieder zurücksetzen, ist die eine Gerade immer noch parallel zur anderen. Das blaue Dreieck liegt jetzt auf der anderen Seite von \(Z\). Wir können die Strahlensätze deshalb auch auf solche Situationen anwenden, wo die Strahlen links und rechts vom Zentrum durch die beiden parallelen Geraden geschnitten werden.

Erster Strahlensatz

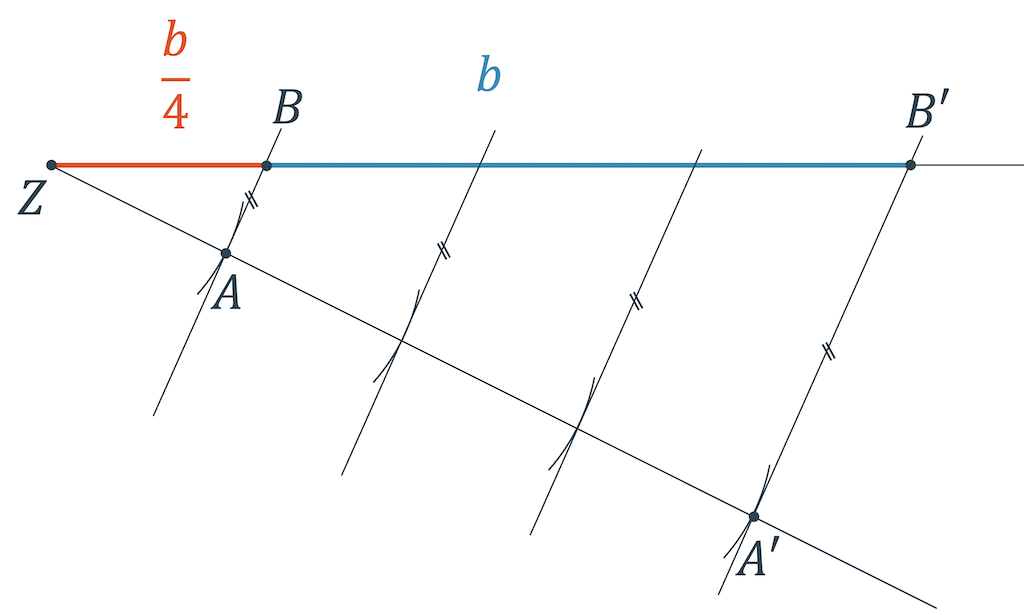
Im Artikel über das Teilen einer Strecke haben wir gelernt, dass eine gegebene Strecke mit Hilfe einer Hilfsgeraden konstruiert werden kann (siehe Abbildung, wo die Strecke durch vier geteilt wird). Wir erkennen, dass die Hilfsgerade als ein zweiter Strahl angesehen werden kann und dass wir auch hier (mindestens) zwei Dreiecke haben: Ein grosses Dreieck mit der blauen Seite (Länge \(b\)) und ein kleines Dreieck mit der roten Seite (Länge \(\frac{b}{4}\)). Das Verhältnis der beiden Seiten ist klar:

\[ \frac{\;\;b\;\;}{\frac{b}{4}} = 4 \]

Das Gleiche gilt natürlich auch auf dem zweiten Strahl der Hilfsgeraden. Dort gilt das gleich Seitenverhältnis zwischen dem grossen und dem kleinen Dreieck. Das Seitenverhältnis auf dem einen Strahl ist gleich, wie das Seitenverhältnis auf dem anderen Strahl. Das gilt immer und bei allen möglichen Verhältnissen, nicht nur wie im gezeigten Beispiel \(4:1\).

Beispiel

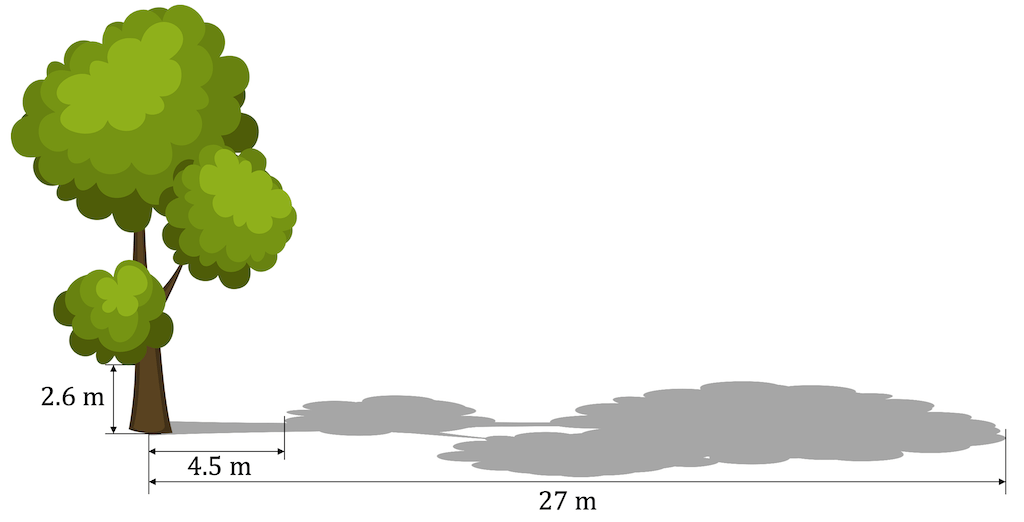
Berechne mit Hilfe des Ersten Strahlensatzes die Höhe des Baums. Funktioniert diese Berechnungsmethode auch, wenn der Baum an einem geraden Hang steht (Schatten am auf- bzw. absteigenden Hang)? Wie begründest du deine Antwort?

---

Wir haben zwei Strahlen: Der erste Strahle geht durch den Baumstamm. An ihm würden wir die Baumhöhe bestimmen. Der zweite Strahl verläuft in der Skizze horizontal im Schatten des Baumstamms. Mit dem Ersten Strahlensatz stellen wir die folgende Gleichung auf, wobei wir für die unbekannte Höhe des Baums \(h\) setzen:

\[ \frac{h}{2.6\;\si{m}} = \frac{27\;\si{m}}{4.5\;\si{m}} \]

Wir lösen nach \(h\) auf und erhalten:

\[ h = 2.6\;\si{m} \cdot \frac{h}{2.6\;\si{m}} = \frac{27\;\si{m}}{4.5\;\si{m}} = \underline{15.6\;\si{m}} \]

Diese Methode funktioniert auch bei einem nicht-horizontalen Boden, d.h. wenn der zweite Strahl etwas ansteigt oder abfällt. Der Erste Strahlensatz gilt unabhängig von der Richtung der Strahlen. Der Grund ist, dass die ähnlichen Dreiecke, die mit den Schnittgeraden entstehen, nicht unbedingt rechtwinklige Dreiecke sein müssen, wie in diesem Beispiel. Sie müssen nicht rechtwinklig sein, um geometrisch ähnlich zu sein. Die geometrische Ähnlichkeit erlaubt uns die Gleichung aufzustellen, die die Streckenverhältnisse auf den Strahlen einander gleichsetzt.

Zweiter Strahlensatz

Der zweite Strahlensatz ist dem ersten Strahlensatz sehr ähnlich. Allerdings bringt er die beiden Strecken auf den parallelen Geraden ins Spiel, die von den beiden Strahlen gebildet werden.

Da die Verhältnisse auf einem einen Strahl gleich sind, wie auf dem anderen Strahl (Erster Strahlensatz), kommt es nicht darauf an, mit welchem Strahl wir vergleichen.

Beispiel

Berechne die Längen \(x\) und \(y\) im folgenden Beispiel

---

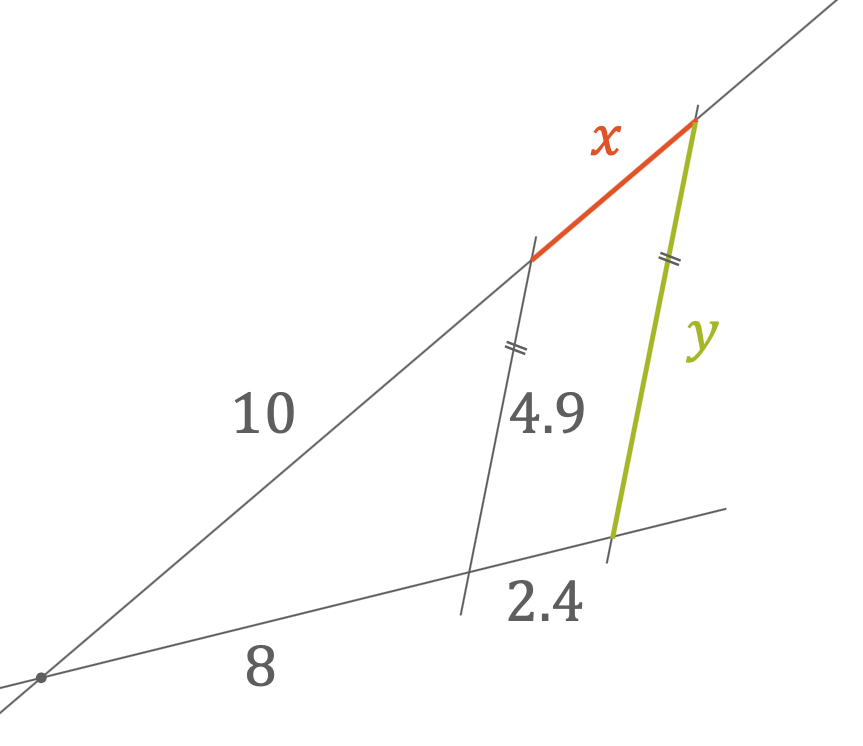
Wir benutzen den Ersten Strahlensatz, indem wir das “grosse Dreieck” und das “kleine Dreieck” vergleichen. Der Strahlensatz liefert uns eine Gleichung:

\[ \frac{8+2.4}{8}=\frac{10+x}{10} \]

Wir lösen nach \(x\) auf, indem wir mit 10 multiplizieren und dann 10 subtrahieren:

\[ x=10 \cdot \frac{10.4}{8} – 10=13-10=\underline{3} \]

Für die Länge \(y\) benutzen wir den Zweiten Strahlensatz, der direkt aus dem gleichen Seitenverhältnis von zwei ähnlichen Dreiecken folgt. Das grosse Dreieck hat die Seite der Länge 10 + 3 = 13 auf dem oberen Strahl. Die entsprechende Seite im kleinen Dreieck hat die Länge 10. Somit gilt:

\[ \frac{y}{13} = \frac{4.9}{10} \]

Wir multiplizieren die Gleichung mit 13 und erhalten:

\[ y = \frac{4.9 \cdot 13}{10} = \underline{6.37} \]