Umkehrung der Strahlensätze

Erster Strahlensatz

Wir erinnern uns, dass der Erste Strahlensatz besagt: “Wenn zwei Strahlen von zwei parallelen Geraden geschnitten werden, dann stehen die Strecken auf den Strahlen im gleichen Verhältnis zueinander.”

Die Umkehrung würde demnach lauten: “Wenn die Strecken auf den Strahlen im gleichen Verhältnis zueinander stehen, dann sind die beiden Geraden, die die Strahlen schneiden, parallel.”

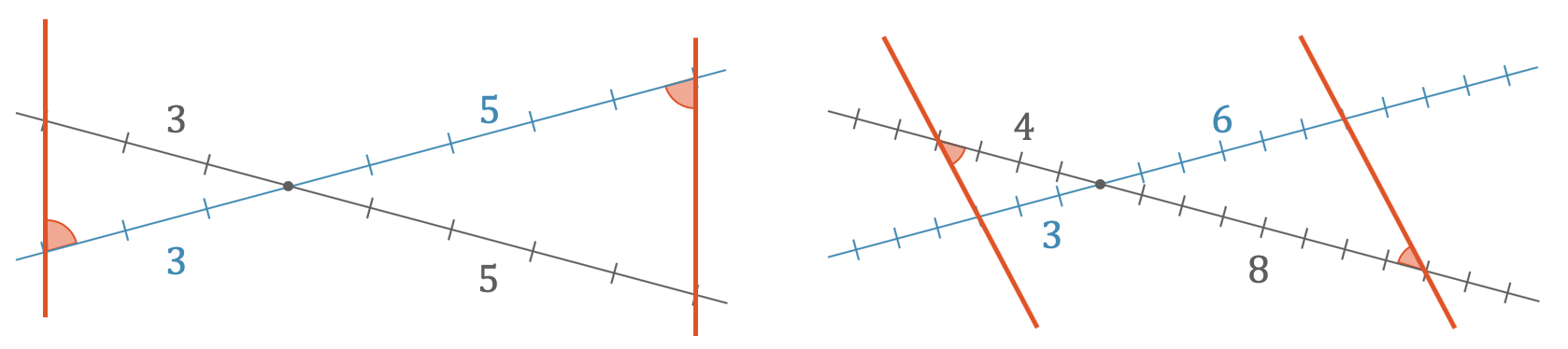
Das funktioniert tatsächlich! In der obigen Abbildung sehen wir, wie in der linken Skizze der blaue Strahl im Verhältnis 3:5 geschnitten wird. Nehmen wir beim anderen Strahl das gleiche Verhältnis, erhalten wir tatsächlich zwei parallele Geraden. Der Grund liegt in der Ähnlichkeit der beiden Dreiecke. Wenn je zwei Seiten eines Dreiecks im Verhältnis stehen, dann ist automatisch auch die dritte Seite im richtigen Verhältnis. Eine weitere Folge ist, dass beide Dreiecke die gleichen Winkel haben müssen.

Zweiter Strahlensatz

Die Umkehrung des Zweiten Strahlensatzes funktioniert nicht einwandfrei. Wir nehmen wieder eine einfache Formulierung des Zweiten Strahlensatzes: “Sind die beiden Geraden parallel, so schneiden Sie die beiden Strahlen so, dass die Strecken auf einem Strahl in gleichem Verhältnis stehen, wie die die Streckenabschnitte auf den beiden Geraden.”

Jetzt drehen wir den Satz um: “Schneiden die beiden Geraden die Strahlen so, dass die Strecken auf einem Strahl im gleichen Verhältnis stehen, wie die Streckenabschnitte auf den beiden Geraden, dann sind die beiden Geraden parallel.”

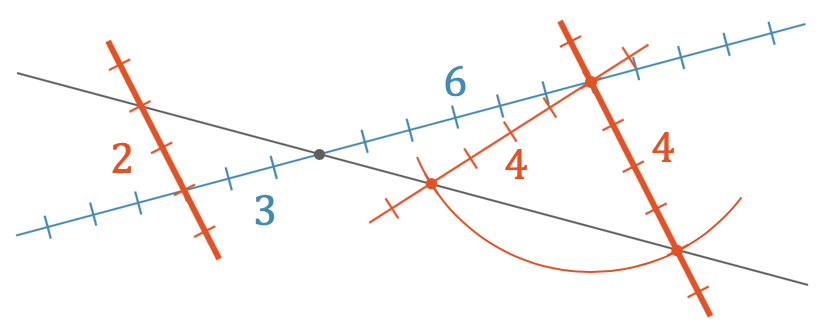
In der folgenden Abbildung sehen wir, wo das Problem liegt. Wir fordern das Verhältnis \(3:2\) bzw. \(6:4\). Für das letzte Stück gibt es aber zwei mögliche Lösungen, die das Verhältnis \(3:2\) bzw. \(6:4\) erfüllen. Tragen wir nämlich die geforderte Länge von 4 mit dem Zirkel ab, kriegen wir zwei Schnittpunkte. Die linke Lösung ist offensichtlich die Richtige – sie ist tatsächlich parallel zur ersten Gerade. Rechts haben wir aber eine sog. Scheinlösung, die definitiv nicht parallel ist.

Der Zweite Strahlensatz kann nicht einfach umgekehrt werden, denn die Umkehrung ist nicht eindeutig. Es handelt sich hier um eine wichtige Erkenntnis aus der Logik. Hierzu vielleicht nicht das beste Beispiel, aber es macht den Umstand deutlicher: “Tom ist ein Kater, also kann er miauen.” Die Umkehrung ist aber nicht eindeutig: “Wenn es miauen kann ist es ein Kater.” Es könnte ja auch eine Katze sein.