Dreieck

Beschreibung

Das Dreieck ist die einfachste Figur von geraden Linien in der Ebene. Dreiecke sind gerade deshalb so wichtig, weil wir sehr viele andere Figuren mit Hilfe von Dreiecken beschreiben können. Ein Viereck ist ja nichts anderes als zwei zusammengesetzte Dreiecke. Ein Fünfeck besteht als zwei Dreiecken usw.

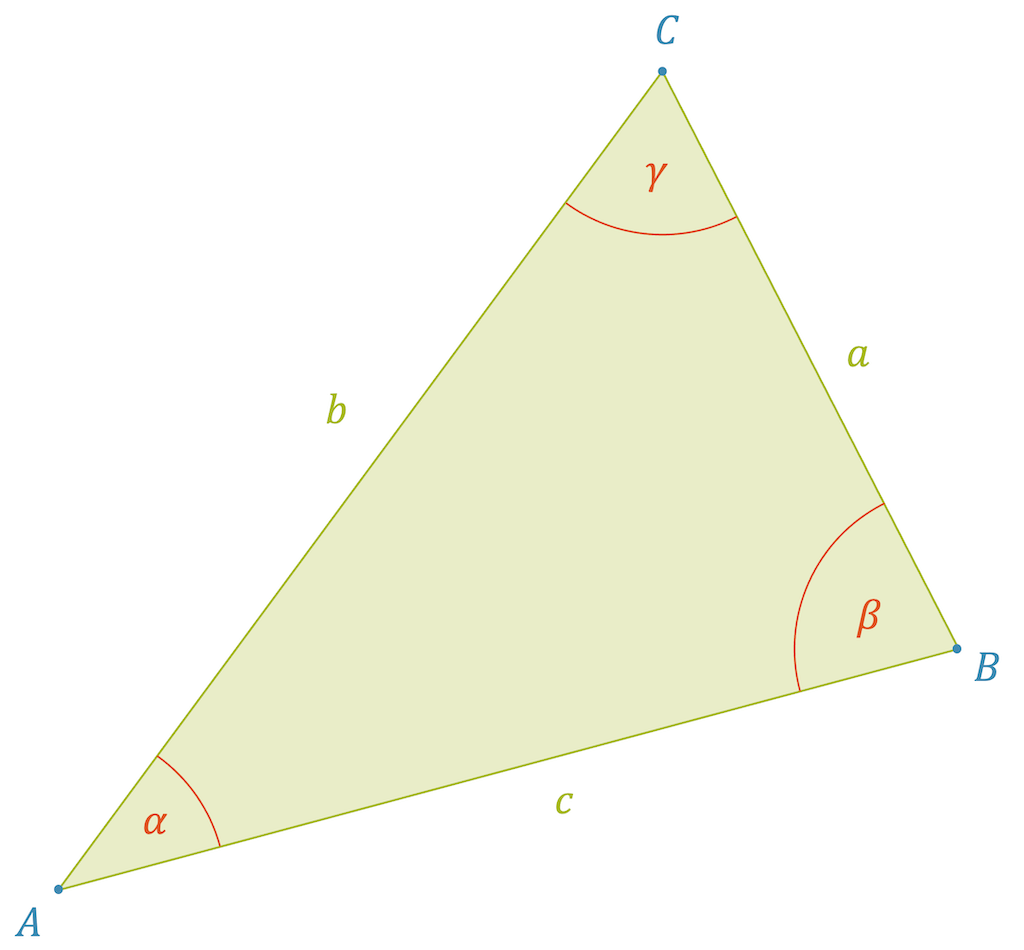
Ein ganz allgemeines Dreieck besteht als folgenden Elementen:

• 3 Eckpunkte: meist nennen wir sie \(A\), \(B\) und \(C\)
• 3 Winkel: meist nennen wir sie \(\alpha\), \(\beta\) und \(\gamma\)
• 3 Seiten: meist nennen wir sie \(a\), \(b\) und \(c\)

Die Bezeichnungen der Eckpunkte werden typischerweise im Gegenuhrzeigersinn vergeben. Die Winkelbezeichnungen passen normalerweise zu den Bezeichnungen der Eckpunkte \(\alpha\) zu \(A\), \(\beta\) zu \(B\) etc. Die Bezeichnungen der Seiten passen zu den gegenüberliegenden Eckpunkten: \(a\) gegenüber \(A\), \(b\) gegenüber \(B\) etc.

Die Winkel der Dreiecke haben eine einfache und unglaublich praktische Eigenschaft: Ihre Summe entspricht für alle Dreiecke immer 180°.

Für die Länge der Dreiecke gibt es ebenfalls eine einfache, für uns jedoch weniger nützliche Gesetzmässigkeit, die sog. Dreiecksungleichung:

Die zwei kürzeren Seiten des Dreiecks sind zusammen länger als die längste Dreiecksseite:

\[ a + b \geq c \]

Im Grenzfall, in welchem sie zusammen gleich lang sind wie die längste Seite, hat das Dreieck keine Fläche mehr und gilt somit nicht mehr als Dreieck.

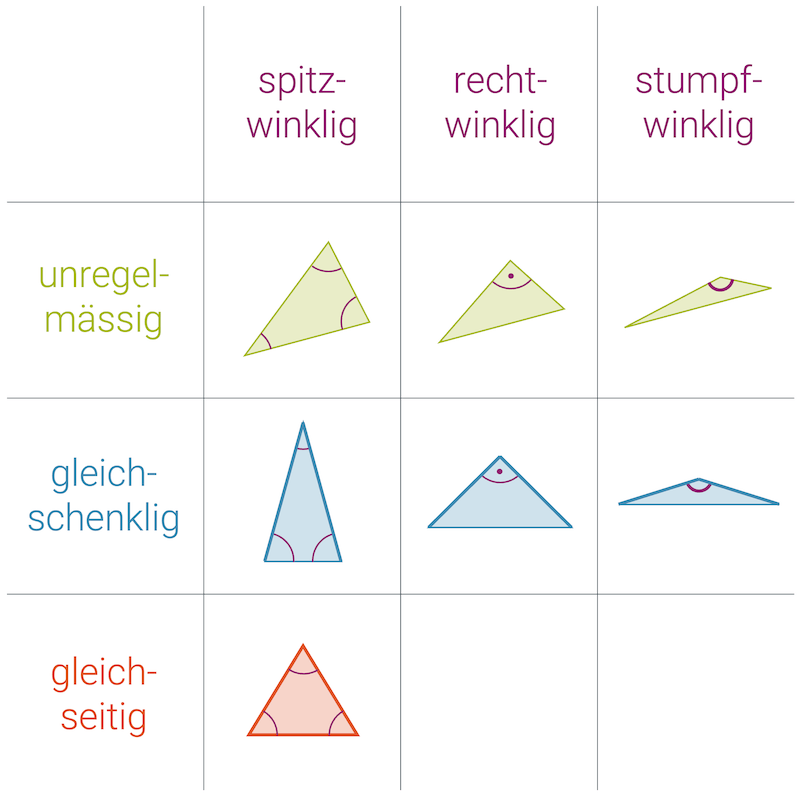
Spezielle Dreiecke

Ein ganz allgemeines Dreieck hat unterschiedlich lange Seiten und spitze Winkel (<90°) und wird deshalb spitzwinklig genannt. Eine sehr wichtige Gruppe der speziellen Dreiecke sind diejenigen, die einen rechten Winkel enthalten. Sie heissen deshalb rechtwinklige Dreiecke. Ist einer der drei Winkel stumpf (>90°), so nennt man das Winkel stumpfwinklig.

Wenn zwei der Seiten gleich lang sind, reden wir von gleichschenkligen Dreiecken. Sie sind besonders praktisch, denn sie haben zwei gleiche Winkel ihre beiden Basiswinkel sind gleich gross.

Das wohl speziellste aller Dreiecke hat drei gleich lange Seiten und hat drei gleich grosse Winkel: das gleichseitige Dreieck.

Mittelsenkrechte und Umkreis

Jedes Dreieck hat einen Umkreis. Das ist ein Kreis, auf welchem alle drei Eckpunkte liegen. Damit ist das Dreieck speziell, denn bei den anderen Polygonen ist das nicht so. Vierecke haben meistens keinen Umkreis und bei Polygonen mit noch mehr Ecken wird es noch unwahrscheinlicher, dass sie einen Umkreis haben. Bei den Dreiecken gibt es aber immer einen Umkreis.

Wir können ihn folgendermassen konstruieren: Ein Kreis ist die Menge aller Punkte, die zu einem Punkt, dem Mittelpunkt \(Z_U\) den gleichen Abstand haben. Dieser Abstand ist der Radius \(r_U\). Die Aussage “Jedes Dreieck hat einen Umkreis” kann somit auch umformuliert werden in: “Jedes Dreieck hat genau einen Punkt \(Z_U\), der zu den drei Eckpunkten den gleichen Abstand hat.” Wie finden wir diesen Punkt?

Wir suchen zuerst mal die Punkte, die zu \(A\) und \(B\) den gleichen Abstand haben. Einer dieser Punkte ist der Seitenmittelpunkt \(M_c\) auf der Seite \(c\). Wir können uns aber auch auf der Mittelsenkrechten von \(c\) bewegen: Alle Punkte auf der Mittelsenkrechten haben den gleichen Abstand zu \(A\) und \(B\).

Von allen Punkten auf der Mittelsenkrechten durch \(M_c\) liegen Punkte, die schon mal zu \(A\) und \(B\) den gleichen Abstand haben. Der Abstand zu \(C\) ist jedoch nicht gleich. Wir wissen aber jetzt schon, dass der gesuchte Punkt \(Z_U\) irgendwo auf dieser Mittelsenkrechten liegen muss!

\[ Z_U \in g_c \]

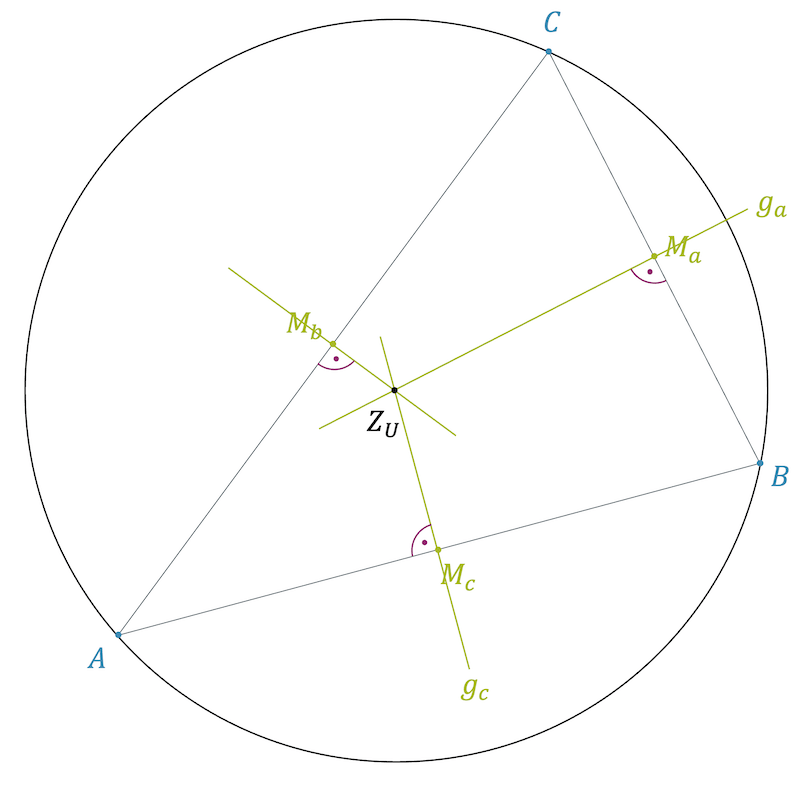
Wir können mit der Seite \(a\) genau gleich vorgehen: Wir erstellen mit der Mittelsenkrechten durch \(M_a\) die Menge aller Punkte, die zu \(B\) und \(C\) den gleichen Abstand haben. Der gesuchte Punkt \(Z_U\) muss auch hier auf dieser Mittelsenkrechten liegen!

\[ Z_U = g_a \]

Die beiden Geraden \(g_c\) und \(g_a\) schneiden sich in einem Punkt. Da die beiden Geraden nichts anderes als Punktmengen sind, können wir diese beiden Mengen schneiden und der Schnittpunkt kann nur \(Z_U\) sein, denn \(Z_U\) ist ein Element beider Mengen. Es ist somit der einzige Punkt, der in der Schnittmenge sein kann.

\[ g_c \cap g_a = \big \{ Z_U \big \} \]

Winkelhalbierende und Inkreis

Jedes Dreieck hat auch einen Inkreis, d.h. einen Kreis, der im Dreieck ist und alle drei Dreiecksseiten berührt. Den Mittelpunkt des Inkreises \(Z_I\) finden wir durch den Schnittpunkt der Winkelhalbierenden.

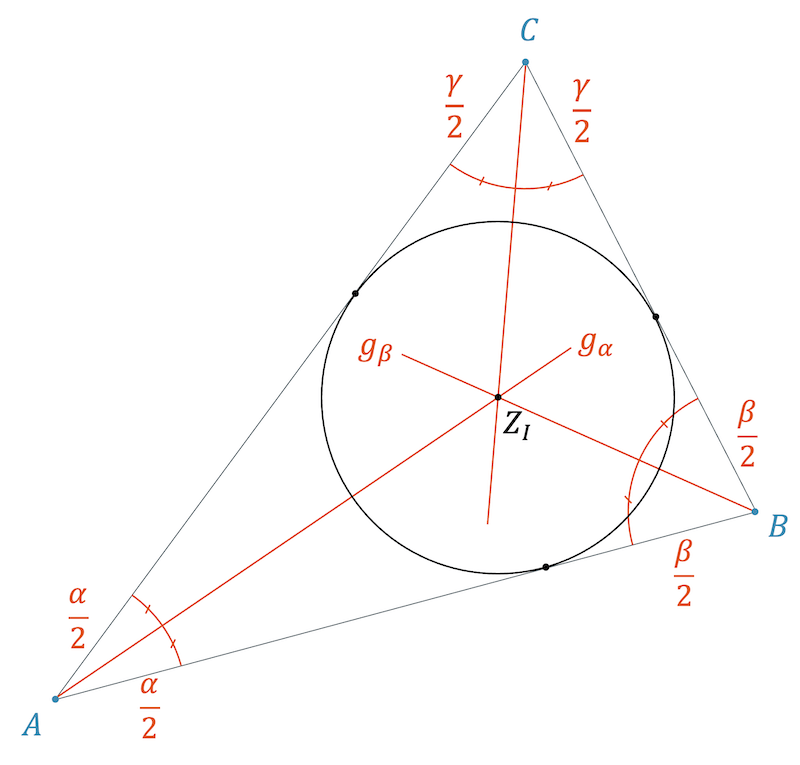
In der nachfolgenden Skizze sehen wir den Inkreis schon eingezeichnet. Wir sehen auch die beiden Berührungspunkte des Inkreises mit den beiden betroffenen Dreiecksseiten. Beide Punkte liegen auf dem Inkreis und haben somit den gleichen Abstand zum Zentrum \(Z_I\). Wenn wir diesen Abstand (Radius) in der Skizze einzeichnen, erhalten wir zwei rechtwinklige Dreiecke, die nachfolgend farbig markiert sind. Die beiden Dreiecke müssen spiegelgleich sein, denn nur so können sie den gleichen Radius als Dreiecksseite haben.

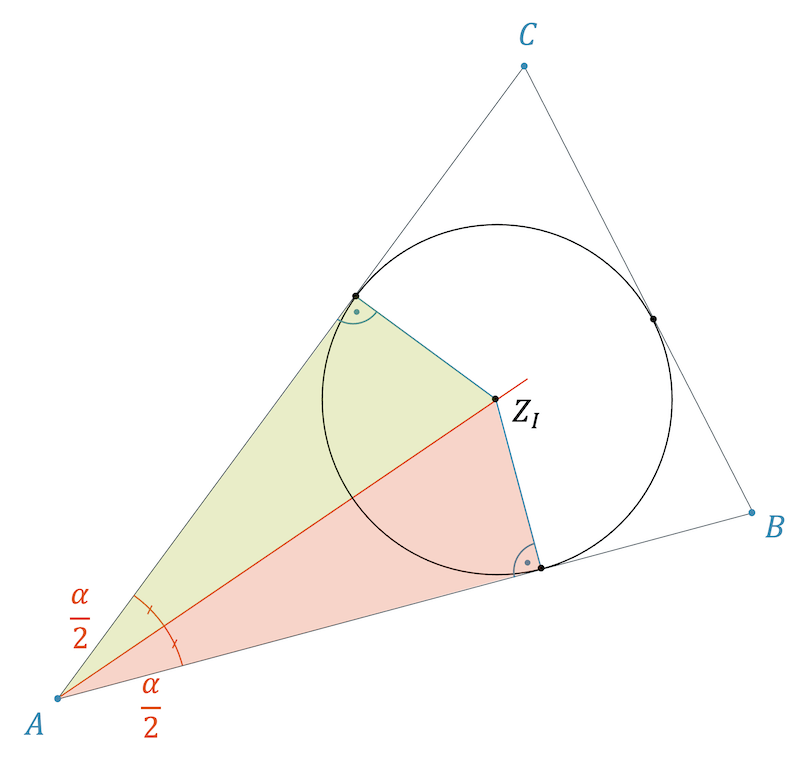
Da das grüne und das rote Dreieck beide den Winkel \(\alpha\) unter sich aufteilen, aber an dieser Stelle den gleichen Winkel haben müssen, ist der Winkel für beide genau \(\frac{\alpha}{2}\). Damit muss \(Z_I\) auf der Winkelhalbierenden liegen:

\[ Z_I \in g_{\alpha} \]

Das Gleiche lässt sich natürlich auch aus Sicht der beiden Dreiecksseiten \(c\) und \(a\) sagen: \(Z_I\) muss auch auf der Winkelhalbierenden \(g_{\beta}\) liegen.

\[ Z_I \in g_{\beta} \]

Wir erhalten das Zentrum zum Inkreis, indem wir zwei Winkelhalbierende schneiden:

\[ g_{\alpha} \cap g_{\beta} = \big \{ Z_I \big \} \]

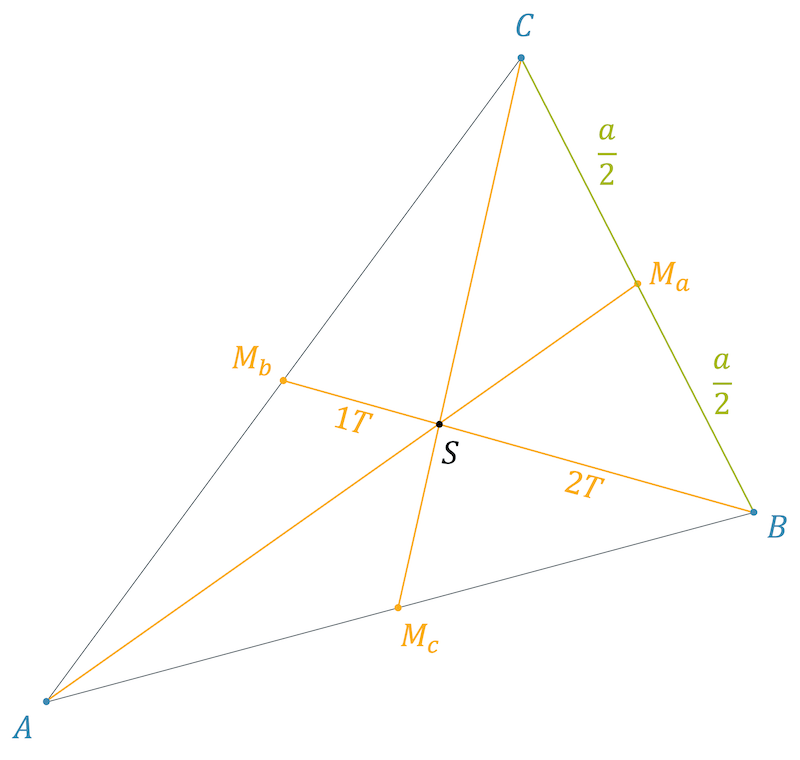
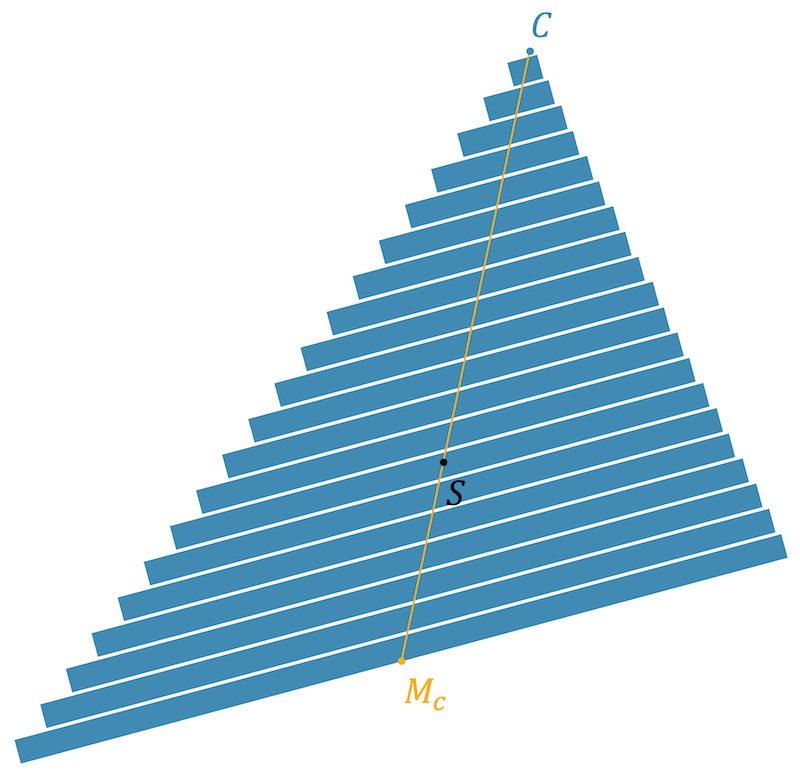
Seitenhalbierende und Schwerpunkt

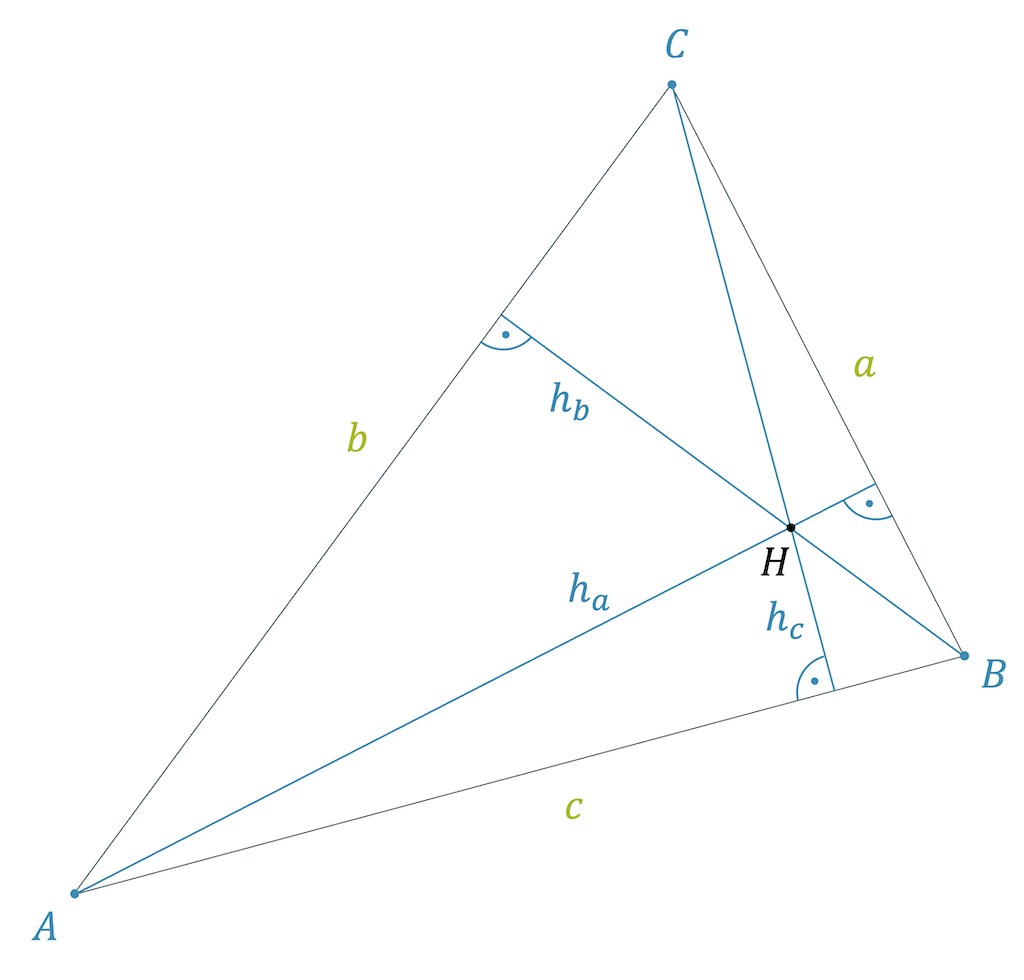
Höhen und Höhenschnittpunkt

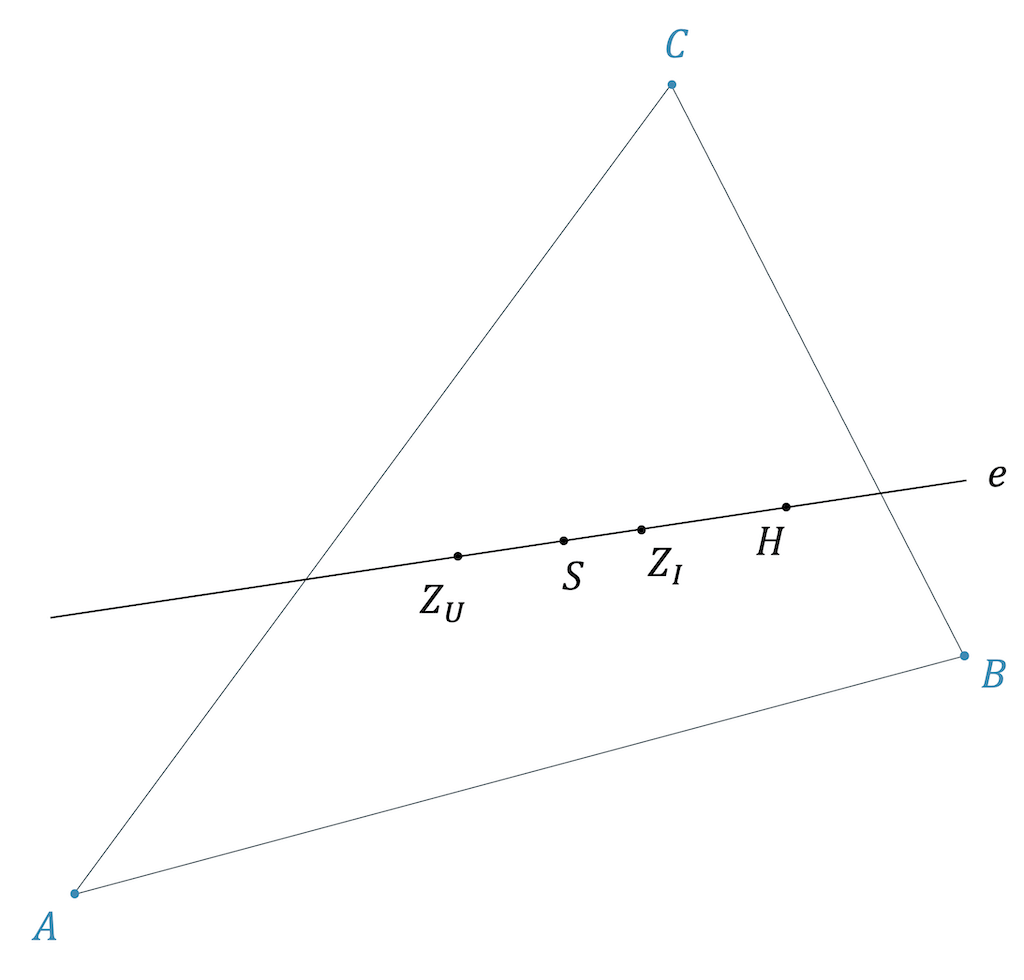
Euler’sche Gerade