Kugel

Kugel finden wir sehr oft in der Natur, meistens aus dem Grund, dass die Kugel der Körper ist, der für ein gegebenes Volumen die kleinst mögliche Oberfläche hat. Aus energetischen Gründen ist das ein Optimum, das z.B. den Wassertropfen, Seifenblasen, Planeten und auch unserer Sonne dann schliesslich die Form gibt. Auch hat die Kugel eine wunderbare Symmetrie, die Kugelsymmetrie. Wir können die Kugel von allen Seiten anschauen und drehen, sie sieht immer gleich aus!

Herleitung des Kugelvolumens

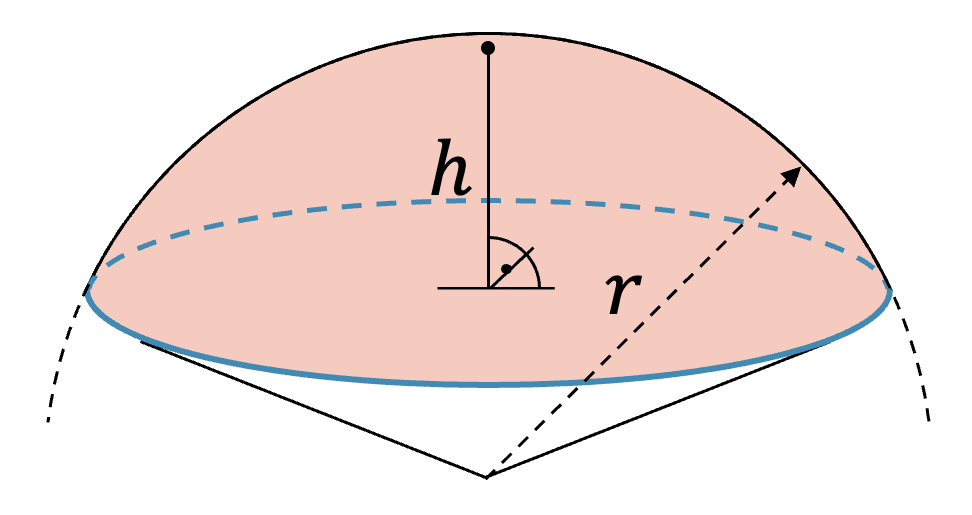
Wir schauen uns eine Halbkugel mit Radius \(r\) an und überlegen uns, welche Fläche ein ebener Schnitt durch die Halbkugel auf der Höhe \(h\) haben würde. Der Schnitt ist ein Kreis, wie jeder ebene Schnitt durch eine Kugel. Wir brauchen deshalb den Radius des Kreises, um seine Fläche zu berechnen. Im Innern der Halbkugel finden wir ein rechtwinkliges Dreieck und mit dem Satz des Pythagoras können wir den Radius \(x\) der Kreisfläche ausrechnen:

\[ x^2 = r^2 – h^2 \]

Somit ist die Kreisfläche in der Halbkugel:

\[ A = \pi x^2 = \pi (r^2 – h^2) \]

Archimedes von Syrakus (287 – 212 v. Chr.) erkannte, dass diese Fläche gleich einer Ringfläche ist, wenn zwei Kreisflächen mit Radien \(r\) und \(h\) voneinander abgezogen werden:

\[ A = \pi (r^2 – h^2) = \pi r^2 – \pi h^2 \]

Das ist eigentlich nicht besonders schwierig. Er erkannte aber zudem, dass man einem Zylinder mit Radius \(r\) und einer Höhe \(r\) einen Kegel herausschneiden kann und wir dann einen Zylinder mit einer kegelförmigen Vertiefung erhalten. Diesen Körper können wir auf der Höhe \(h\) eben schneiden und kriegen die Ringfläche mit der betragsmässig genau gleich grosse Fläche, wie die Kreisfläche in der Halbkugel.

Wir haben somit eine Halbkugel, deren Schnittfläche auf beliebiger Höhe \(h\) gleich gross ist, wie der Schnitt durch einen ein Zylinder mit Kegelvertiefung, der ebenfalls auf beliebiger Höhe \(h\) geschnitten wird. Jetzt nehmen wir das Prinzip von Cavalieri zum Zug: Auf der einen Seite haben wir einen Stapel von Kreisflächen, bis wir das Volumen einer Halbkugel erhalten. Auf der anderen Seite haben wir einen Stapel von Ringen, die zusammen das Volumen einer Zylinders mit Kegelvertiefung erzeugen.

Da die einzelnen “Blätter” auf einer bestimmten Höhe immer die gleiche Fläche haben und es auf beiden Seiten die gleich Anzahl “Blätter” hat, müssen die beiden Volumina von Halbkugel und Zylinder mit Kegelvertiefung gleich gross sein!

Das Volumen der Kugel kennen wir noch nicht, aber das Volumen eines Zylinders und eines Kegels können wir sehr wohl berechnen. Dazu brauchen wir nur die Grundfläche (beide Male \(\pi r^2\)) und die Höhe (beide Male \(r\)):

\[ V_{\text{Zylinder}} = \pi r^2 \cdot r = \pi r^3 \]

\[ V_{\text{Kegel}} = \frac{1}{3} \cdot \pi r^2 \cdot r = \frac{1}{3} \pi r^3 \]

Für den Zylinder mit Kegelvertiefung müssen wir nur das Volumen des Kegels vom Zylinder abziehen:

\[ V = V_{\text{Zylinder}} – V_{\text{Kegel}} = \frac{2}{3} \pi r^3 \]

Das ist also das Volumen der Halbkugel. Wir verdoppeln es und erhalten das Volumen der Kugel mit Radius \(r\):

\[ V = \frac{4}{3} \pi r^3 \]

Herleitung der Kugeloberfläche

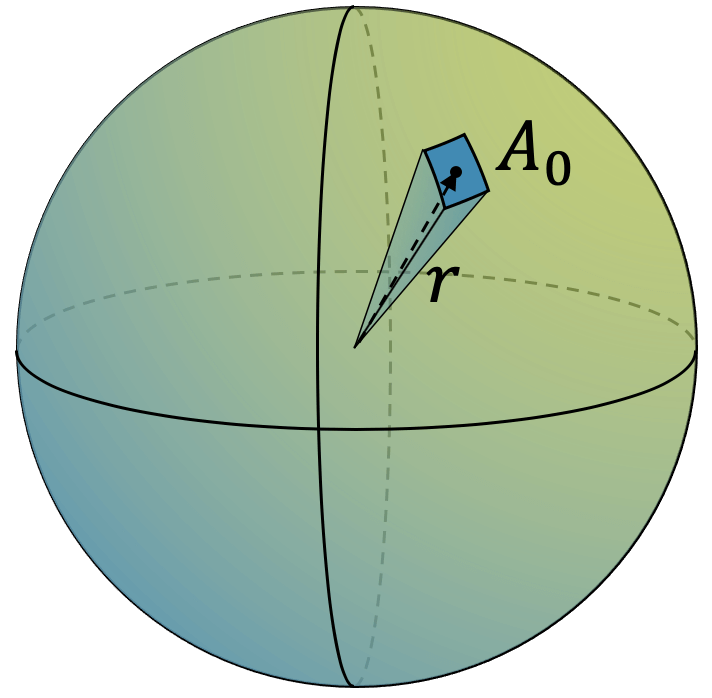
Wir können die Oberfläche einer Kugel mit Hilfe des Volumens herleiten. Statt aus einem zweidimensionalen Kuchen ein dünnes Stück herauszuschneiden, schneiden wir eine Pyramide aus der Kugel heraus. Diese sehr dünne Pyramide hat eine sehr kleine Grundfäche \(A_0\). Wir stellen uns vor, dass die Pyramide so dünn ist, dass die Grundfläche eigentlich fast flach ist. Die Höhe dieser Pyramide ist \(r\). Auf diese Weise können wir für das Volumen \(V_0\) der Pyramide schreiben:

\[ V_0 = \frac{1}{3} A_0 r \]

Je kleiner \(A_0\) ist, desto dünner wird die herausgeschnittene Pyramide und je mehr solche Pyramiden stecken in der Kugel. Wir wissen nicht wie viele solche Pyramiden die ganze Kugel ausmachen, aber es ist eine sehr grosse Zahl \(n\), eigentlich \(n \rightarrow \infty\). Für das Volumen der Kugel gilt:

\[ V = \frac{4}{3} \pi r^3 = n \cdot V_0 = n \cdot \frac{1}{3} A_0 r \]

Wir erhalten so eine Gleichung:

\[ \frac{4}{3} \pi r^3 = n \cdot \frac{1}{3} A_0 r \]

Wir lösen nach \((n A_0)\) auf und erhalten so die Oberfläche der Kugel \(O\), denn die \(n\) Grundflächen ergeben zusammen ja die ganze Oberfläche:

\[ n \cdot A_0 = O = 4 \pi r^2 \]

Schnitt mit einer Ebene

Die Kugel ist vom Prinzip her ein Kreis mit einer zusätzlichen Dimension. Der Kreis zeichnet sich dadurch aus, dass alle Punkte auf dem Kreis den gleichen Abstand \(r\) zum Kreiszentrum haben. Wenn wir nur zwei Dimensionen zulassen, erhalten wir einen Kreis in der Ebene, die durch die beiden Koordinaten aufgespannt wird. Wenn wir jetzt aber drei Dimensionen zulassen, ergibt sich eine Kugel mit allen Punkten, die den Abstand \(r\) zum Zentrum der Kugel haben.

Wir können auch mit der dreidimensionalen Kugel beginnen und sagen, dass wir bei einem Schnitt mit einer Ebene im Prinzip eine Dimension wegnehmen und dadurch zu einem Kreis kommen. Tatsächlich ist jeder ebene Schnitt mit einer Kugel immer ein Kreis! Den Kreisradius \(\rho\) können wir für jeden Schnitt mit dem Satz des Pythagoras berechnen, wenn wir wissen, welchen Abstand die Schnittebene vom Kugelzentrum hat.

Zwei Kugeln schneiden sich ebenfalls in einem Kreis. Sie teilen ihre gemeinsame Schnittebene, die bei beiden Kugeln den gleichen Kreis erzeugt. Wir kennen diese Formation von Seifenblasenpaaren.

Beispiel

Ein Schale wurde aus zwei Halbkugeln mit Radien \(r\) und \(\rho\) geformt. Berechne das Volumen des Schalenkörpers.

---

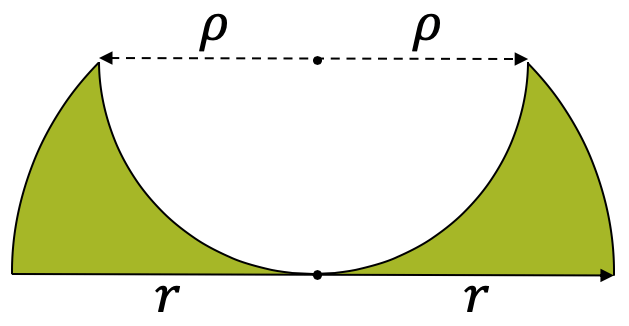
Die Schale wurde zuerst aus einer grossen Halbkugel geformt mit dem Volumen \(V_1\):

\[ V_1 = \frac{1}{2} \cdot \frac{4}{3} \pi r^3 = \frac{2}{3} \pi r^3 \]

Aus dieser Halbkugel wurde eine kleinere Halbkugel mit dem Volumen V_2 und Radius \(\rho\) weggenommen:

\[ V_2 = \frac{1}{2} \cdot \frac{4}{3} \pi \rho^3 = \frac{2}{3} \pi \rho^3 \]

Das Volumen des Schalenkörpers ist demnach:

\[ V = V_1 – V_2 = \frac{2}{3} \pi r^3 – \frac{2}{3} \pi \rho^3 = \frac{2}{3} \pi \big(r^3 – \rho^3 \big) \]

Wenn wir den Radius \(\rho\) auch in der vertikalen Achse des Schalenkörpers eintragen, erkennen wir ein rechtwinkliges Dreieck mit den beiden Katheten \(\rho\) und der Hypotenuse \(r\). Gemäss Satz des Pythagoras gilt damit:

\[ \rho^2 + \rho^2 = r^2 \quad \rightarrow \quad \rho = \frac{r}{\sqrt{2}} \]

Wir setzen diesen Ausdruck in die Gleichung für das Volumen ein:

\[ V = \frac{2}{3} \pi \Big(r^3 – ( \frac{r}{\sqrt{2}})^3 \Big) = \underline{\frac{2}{3} \pi r^3 \Big( 1 – \frac{1}{\sqrt{8}} \Big)} \]