Laplace-Experimente

Mit Laplace-Experimenten meinen wir Zufallsversuche, die die ganz bestimmte Eigenschaft besitzen, dass ihre Ergebnisse alle die gleiche Wahrscheinlichkeit haben. Das macht die Rechnung meist einfacher oder überhaupt erst möglich. In sehr vielen Fällen können wir ein Zufallsexperiment als Laplace-Experiment behandeln und entsprechend die Wahrscheinlichkeiten für die einzelnen Ergebnisse alle gleich setzen. Die Laplace-Experimente sind nach Pierre-Simon Laplace (1749 – 1827) benannt, einem französischen Mathematiker.

Wenn wir nochmals das Histogramm nehmen von einem Würfelversuch, dieses Mal aber mit den theoretischen Wahrscheinlichkeiten statt den gemessenen relativen Häufigkeiten, so erhalten wir das typische Bild für ein Laplace-Experiment: Alle Elementarereignisse haben die gleiche Wahrscheinlichkeit. Wir sprechen hier auch von einer sog. Gleichverteilung der Wahrscheinlichkeiten. Damit ist gemeint, dass jede Augenzahl die gleiche Wahrscheinlichkeit erhält, denn diese wurde allen Elementarereignisse gleich verteilt.

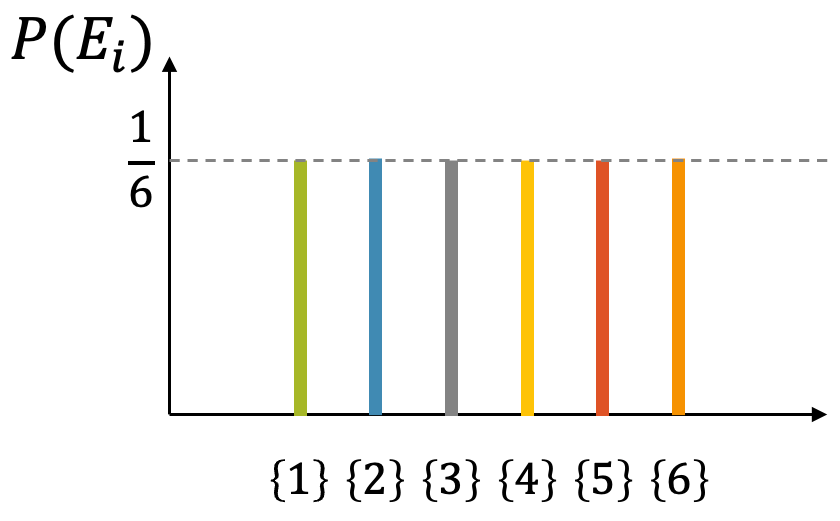
Wir erinnern uns noch daran, dass alle Elementarereignisse zusammen den Ergebnisraum füllen. In diesem einfachen Fall gilt:

\[ E_1 \cup E_2 \cup E_3 \cup E_4 \cup E_5 \cup E_6 \;\; = \;\; \bigcup_{i=1}^6 \Big( E_i \Big) \;\; = \;\; \Omega \]

Da wir hier Elementarereignisse anschauen und diese per Definition disjunkt sind, d.h. sich nicht überschneiden, sind ihre Wahrscheinlichkeiten ganz einfach additiv, ohne dass wir uns über die Schnittmenge Sorgen machen müssen. Es gilt somit:

\[ P(E_1) + P(E_2) + P(E_3) + P(E_4) + P(E_5) + P(E_6) \;\; = \;\; \sum_{i=1}^6 P(E_i) \;\; = \;\; P(\Omega) = 1 \]

Die Summe aller Säulen im Histogramm muss deshalb 1 ergeben. Da die Wahrscheinlichkeiten im Laplace-Experiment alle gleich sind, können wir statt addieren, einfach eine Wahrscheinlichkeit mit der Anzahl Ergebnisse multiplizieren:

\[ 6 \cdot P(E_i) = 1 \quad \rightarrow \quad P(E_i) = \frac{1}{6} \]

Im allgemeinen Fall eines Laplace-Experimentes gilt deshalb:

\[ P(E_i) = \frac{1}{\big| \; \Omega \; \big|} \]

Die Mächtigkeit des Ergebnisraums gibt uns an, wie viele Elementarereignisse möglich sind. Da diese alle die gleiche Wahrscheinlichkeit haben, ist deren Wahrscheinlichkeit einfach 1 durch ihre Anzahl.

Beispiel

Ein Spieler versucht sein Glück beim amerikanischen Roulette. Er setzt auf schwarz und auf das mittlere Drittel der Zahlen, nämlich 13 bis 24. Wie gross ist die Wahrscheinlichkeit zu gewinnen? Hätte er ein anderes Drittel wählen sollen?

---

Wenn der Roulettekessel fair ist, dann sind alle Zahlen 1 bis 36 und die beiden Nullen “0” und “00” alle gleich wahrscheinlich, woraus folgt, dass es sich um ein Laplace-Experiment handelt. Wir haben 38 Elementarereignisse und somit ist die Wahrscheinlichkeit für ein Elementarereignis:

\[ P(E_i) = \frac{1}{38} = 2.63 \% \]

Das ist gleichzeitig auch die Wahrscheinlichkeit, mit einer gesetzten Zahl zu gewinnen. Der Spieler hat auf schwarz und auf das mittlere Drittel gesetzt. Die für ihn gewinnenden Zahlen ergeben das gewünschte Ereignis \(A\):

\[ A = \Big\{ 13, 15, 17, 19, 20, 22, 24 \Big\} \]

Die Mächtigkeit des gewünschten Ereignisses \(A\) ist: \(\big| A \big| = 7\). Das bedeutet, dass es 7 günstige Elementarereignisse gibt, deren einzelne Wahrscheinlichkeiten sich addieren. Damit wird die Wahrscheinlichkeit mit dieser Wette zu gewinnen:

\[ P(A) = 7 \cdot \frac{1}{38} = \underline{18.4 \%} \]

Wir sehen schnell, dass er \underline{das richtige Drittel} gewählt hat. Das erste Drittel hat nur 6 gewünschte Elementarereignisse und das dritte Drittel nur noch deren 5. 

Weil die Anzahl Elementarereignisse für die Berechnung von Wahrscheinlichkeiten in Laplace-Experimenten so wichtig ist, entstand innerhalb der Stochastik das Teilgebiet der Kombinatorik. Mit ihrer Hilfe können wir die Anzahl Elementarereignisse korrekt bestimmen und so auch komplexere Laplace-Experimente berechnen.