Das Wichtigste in Kürze
Im folgenden sind die Ähnlichkeitssätze für Dreiecke aufgelistet. Dabei werden die Grössen von den zwei Dreiecken $ABC$ und $A’B’C’$ verglichen:
W:W:W-Satz
Zwei Dreiecke mit drei gleichen Winkeln sind geometrisch ähnlich:
\[ \alpha = \alpha’ \quad \text{und} \quad \beta = \beta’ \quad (\text{und} \quad \gamma = \gamma’) \]
S:S:S-Satz
Zwei Dreiecke sind geometrisch ähnlich, wenn die drei Seitenverhältnisse gleich sind:
\[ \frac{a}{a’} = \frac{b}{b’} = \frac{c}{c’} \]
S:W:S-Satz
Zwei Dreiecke sind geometrisch ähnlich, wenn zwei Seitenverhältnisse gleich sind, sowie der von den betreffenden Seiten eingeschlossene Winkel gleich ist:
\[ \frac{b}{b’} = \frac{c}{c’} \quad \text{und} \quad \alpha = \alpha’ \]
S:S:W-Satz
Zwei Dreiecke sind geometrisch ähnlich, wenn die zwei Seitenverhältnisse und die Winkel gegenüber der jeweils grössten Seite gleich sind:
\[ \frac{b’}{b} = \frac{c’}{c} \quad \text{und} \quad \gamma = \gamma’ \]
Dabei ist mit $c$ die grösste Seite im Dreieck gemeint.
Video
-
Please login for access. Login
Häufigste Fragen
Wir wissen, dass zwei Dreiecke geometrisch ähnlich sind, wenn ihre drei Winkel übereinstimmen und wenn ihre Seiten proportional sind. Oft ist es aber so, dass wir nicht diese ganzen Informationen zur Verfügung haben und wir trotzdem wissen möchten, ob zwei Dreiecke ähnlich sind oder nicht.
W:W:W-Satz
Der erste Ähnlichkeitssatz ist nach den drei Winkeln benannt. Eigentlich reicht es, wenn wir nur zwei Winkel kennen. Der dritte Winkel kann ja mit der Winkelsumme von 180° im Dreieck berechnet werden. Trotzdem wird der Satz mit 3 “W”s bezeichnet:
W:W:W-Satz: Die zwei Dreiecke \(ABC\) und \(A’B’C’\) mit drei gleichen Winkeln sind geometrisch ähnlich:
\[ \alpha = \alpha’ \quad \text{und} \quad \beta = \beta’ \quad (\text{und} \quad \gamma = \gamma’) \]
Beispiel
Zeige mit Hilfe des W:W:W-Satzes, dass die beiden Dreiecke \(ABC\) und \(A’B’C’\) geometrisch ähnlich sind.
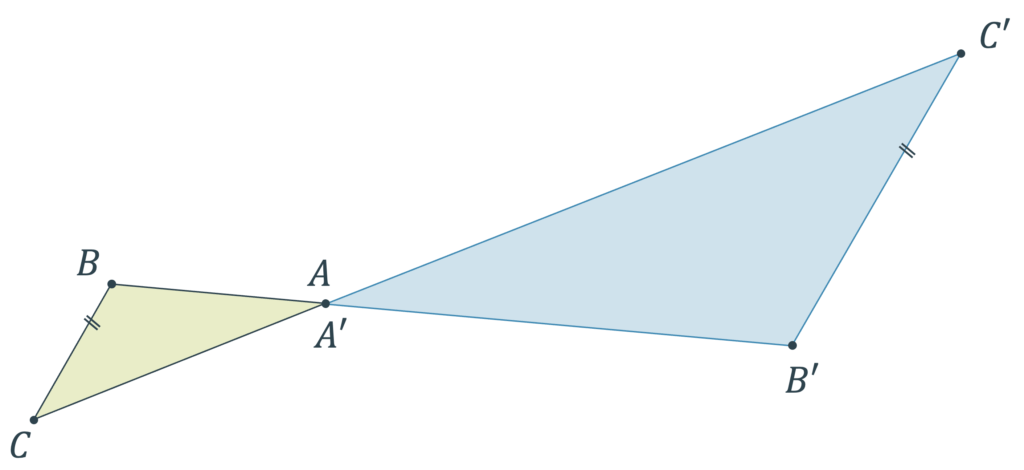
S:S:S-Satz
Beim S:S:S-Satz geht es um Seiten-Verhältnisse. Geometrisch ähnliche Dreiecke können verschieden gross sein, d.h. die Seiten müssen nicht gleich gross sein, wie bei den Kongruenzsätzen.
Die Proportionen müssen gleich sein, d.h. die Verhältnisse der Seiten zueinander oder die Verhältnisse der Seiten zwischen den beiden Dreiecken, müssen immer gleich sein, damit zwei Dreiecke ähnlich sind.
S:S:S-Satz: Zwei Dreiecke \(ABC\) und \(A’B’C’\) sind geometrisch ähnlich, wenn die drei Seitenverhältnisse gleich sind. Wir können die entsprechenden Seiten bei den beiden Dreiecken miteinander verlgleichen…
\[ \frac{a}{a’} = \frac{b}{b’} = \frac{c}{c’} \]
…oder wir betrachten die Verhältnisse der Seiten im Dreieck selbst:
\[ \frac{a}{b} = \frac{a’}{b’} \qquad \qquad \frac{a}{c} = \frac{a’}{c’} \qquad \qquad \frac{b}{c} = \frac{b’}{c’} \]
Beispiel
Beweise, dass die beiden Dreiecke ähnlich sind.
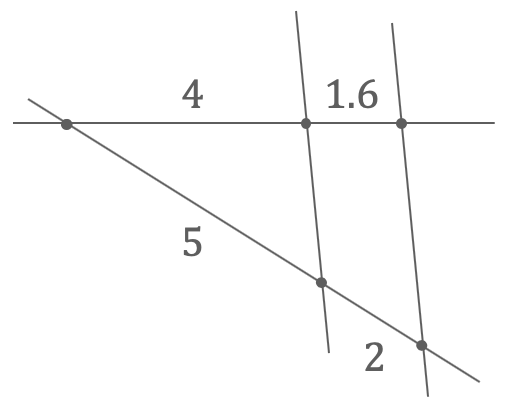
“Wenn wir nur zwei Seitenverhältnisse kennen, brauchen wir noch einen Winkel…aber nicht irgendeinen Winkel!”
S:W:S-Satz
Wenn wir nur zwei Seitenverhältnisse haben, brauchen wir eine dritte Information, um über die Ähnlichkeit von zwei Dreiecken eine Aussage machen zu können.
Haben wir den Winkel zwischen den beiden Seiten, von welchen wir das Seitenverhältnis kennen, dann können wir die Ähnlichkeit mit dem S:W:S-Satz beweisen.
Beachte: Es klappt nicht mit einem anderen Winkel! Hier gibt es mehrere Lösungen, wobei gewisse Scheinlösungen geometrisch nicht ähnlich sind, obwohl die beiden (fälschlicherweise) betrachteten Winkel gleich sind.
S:W:S-Satz: Zwei Dreiecke sind geometrisch ähnlich, wenn die zwei Seitenverhältnisse und gleich sind, sowie die von den betreffenden Seiten eingeschlossenen Winkel gleich sind:
\[ \frac{b}{b’} = \frac{c}{c’} \quad \text{und} \quad \alpha = \alpha’ \]
Schauen wir uns nochmals kurz das Bild aus dem vorigen Beispiel an:

Hier haben wir auch nur zwei Seitenverhältnisse gegeben. Allerdings gibt uns die Skizze noch eine zusätzliche Information, nämlich dass der eingeschlossene Winkel zwischen den beiden Strahlen gleich ist. Damit hatten wir eigentlich eine SWS-Aufgabe.
Beispiel
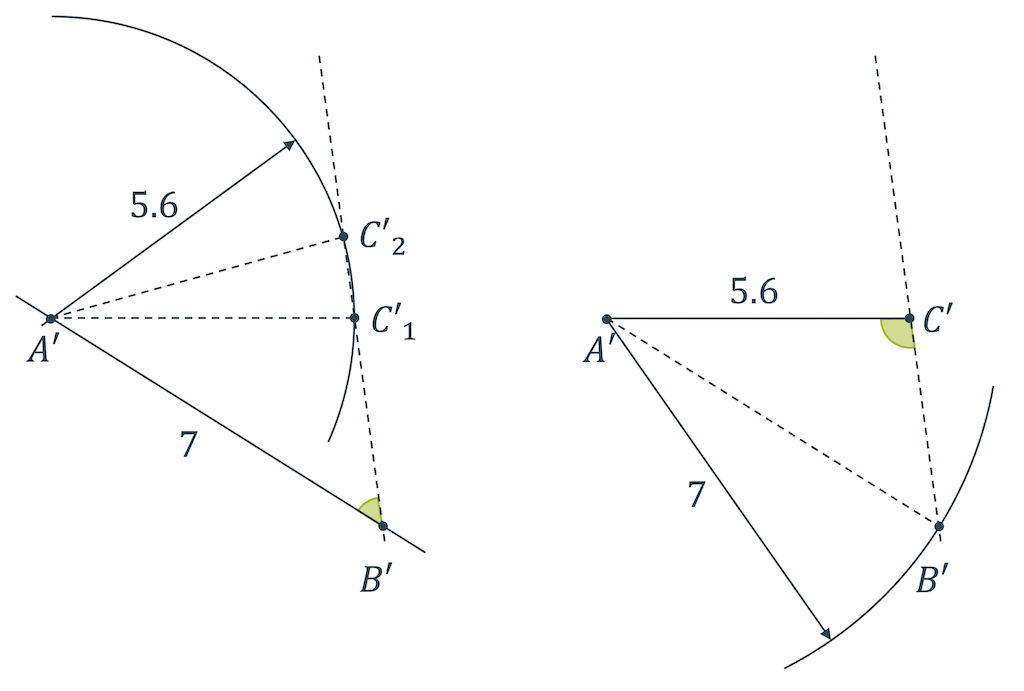
Zeige mit einer Skizze, dass nebst den zwei gleichen Seitenverhältnissen, unbedingt der eingeschlossene Winkel gleich sein muss und es bei einem anderen Winkel zu Scheinlösungen kommt, die nicht geometrisch ähnlich sind.
S:S:W-Satz
Wenn wir nur zwei Seitenverhältnisse haben, können wir die dritte Information auch vom Winkel kriegen, der gegenüber der grösseren Seite ist.
S:S:W-Satz: Zwei Dreiecke sind geometrisch ähnlich, wenn die zwei Seitenverhältnisse und der Winkel gegenüber der jeweils grössten Seite im Dreieck gleich sind:
\[ \frac{b’}{b} = \frac{c’}{c} \quad \text{und} \quad \gamma = \gamma’ \]
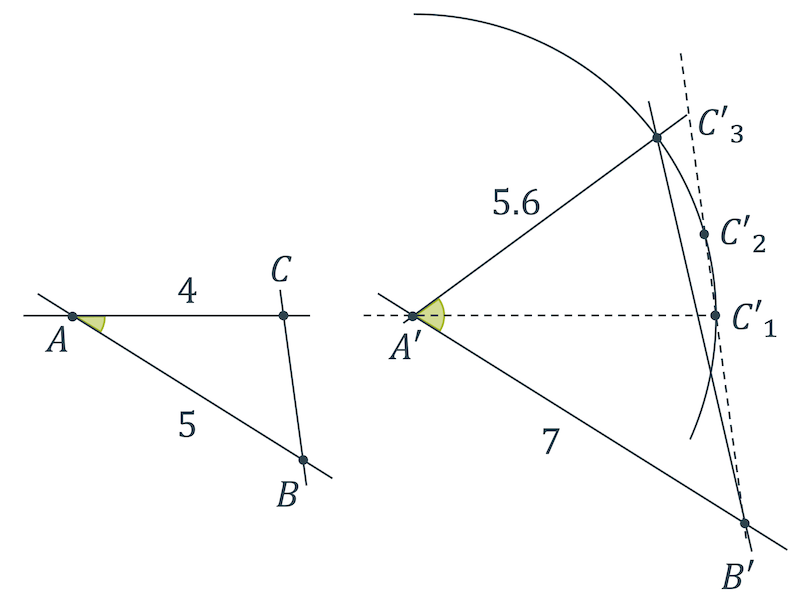
In der nachfolgenden Grafik (links) wird gezeigt, dass ein gleicher Winkel (hier \(\beta’\)) gegenüber einer kürzeren Seite, zu mehreren Lösungen führt (links).
In der Grafik rechts ist der Winkel aber gegenüber der grösseren Seite (hier \(\gamma’\)). Es gibt nur eine eindeutige Lösung.
Beachte, dass der andere Schnittpunkt des Kreisbogens mit der gestrichelten Linie weiter oben zwar zu einem anderen Dreieck führt, das aber keine gültige Lösung darstellt. Nehmen wir nämlich den anderen Punkt, so wird die mit dem Radius 7 abgetragene Seite nicht zu einer Seite \(c’\), sondern zu einer Seite \(b’\), für die ein anderes Seitenverhältnis gilt. Sie hat somit nicht die Länge 7.
Lernziele
- Du kennst die vier Ähnlichkeitssätze für Dreiecke (auswendig) und kannst sie in eigenen Worten erklären.
- Du kannst Dreiecke bezüglich ihrer Ähnlichkeit mit Hilfe der vier Ähnlichkeitssätze analysieren.
Weitere Links
Ähnlichkeitssätze für Dreiecke (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.