Zahl π

Herleitung der Annäherung durch Archimedes

Wie können wir den Kreisumfang berechnen? Offensichtlich ist der Umfang eines Kreises \(U\) abhängig von seinem Radius bzw. Durchmesser \(d\). Je grösser der Kreis, desto grösser sein Umfang. Wenn wir die einfach zu berechnenden geometrischen Formen des gleichseitigen Dreiecks, Quadrats oder regelmässigen Fünfecks nehmen, so ist der Umfang \(3s, 4s\) bzw. \(5s\), wobei \(s\) die Seitenlänge ist. Wenn wir bei diesen Figuren die Seitenlänge \(s\) verdoppeln, würde sich auch der Umfang \(U\) verdoppeln.

Das gleiche ist auch beim Kreis zu erwarten. Ein doppelter Durchmesser sollte zu einem doppelten Umfang führen. Daraus folgt, dass das Verhältnis zwischen Umfang und Durchmesser immer gleich sein müsste, d.h. gleich einer Zahl ist.

Diese Zahl heisst ”pi” und wird mit dem griechischen Buchstaben \(pi\) geschrieben (\(pi\) ist das ”p” des griechischen Alphabets):

[ pi = frac{U}{d} = 3.141592654… ]

Erstaunlicherweise ist das Verhältnis zwischen Umfang und Durchmesser tatsächlich immer genau gleich, jedoch ist diese Zahl keine ”schöne” Zahl, sondern eine irrationale Zahl, d.h. eine Zahl, die wir nicht 100%-ig genau hinschreiben können. Der aktuelle Rekord (2020) liegt bei einer Beschreibung der Zahl mit 50 Billionen Nachkommastellen!

Die Zahl \(pi\) war bereits im 16. Jahrhundert v.Chr. im Alten Ägypten bekannt, wenn auch noch in einer relativ groben Näherung \(3.1605\), d.h. auf eine Stelle genau richtig. Dem griechischen Mathematiker, Physiker und Ingenieur Archimedes von Syrakus (im heutigen Sizilien) gelang eine Annäherung auf zwei Stellen nach dem Komma, d.h. er formulierte eine Ober- und eine Untergrenze für die Zahl \(pi\):

[ 3.1408450 approx Big( 3+frac{10}{71} Big) quad < quad pi quad < quad Big( 3+frac{10}{70} Big) approx 3.1428571 ]

Archimedes’ Gedankenexperiment werden wir genauer anschauen, denn es ist wirklich sehr schön und kann mit den trigonometrischen Funktionen berechnet werden.

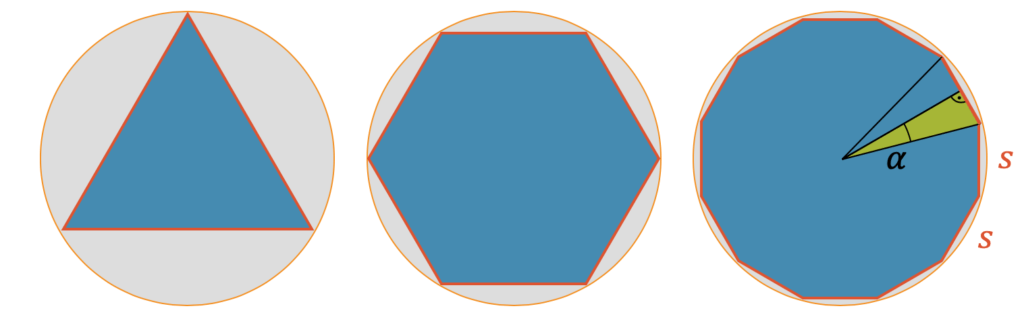
Wenn wir die Evolution von einem gleichseitigen Dreieck zu einem gleichseitigen Sechseck zu einem gleichseitigen Zwölfeck anschauen, dann sehen wir, dass das regelmässige \(n\)-Eck sich immer mehr dem Kreis annähert, je mehr Ecken es hat. Archimedes’ Idee war deshalb, je weiter wir mit der Eckzahl hochgehen, desto näher kommen wir dem Mysterium des perfekten Kreises heran, auch wenn wir es erst in der Unendlichkeit tatsächlich erreichen würden. Wir nehmen die Idee von Archimedes auf und berechnen den Umfang des regelmässigen \(n\)-Ecks. Allerdings werden wir diese Berechnung mit Hilfe der trigonometrischen Funktionen machen.

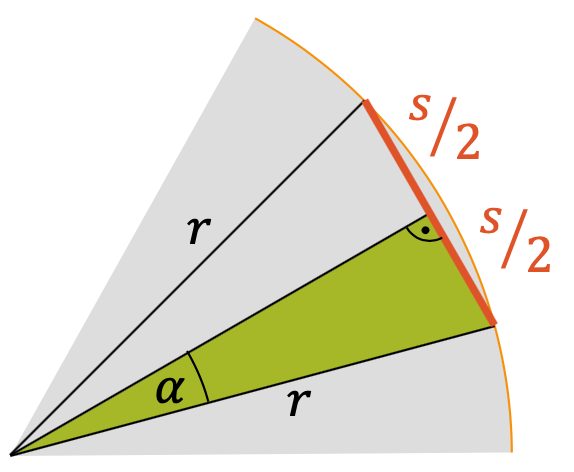
Wir schauen uns dazu einen Ausschnitt aus dem regelmässigen \(12\)-Eck an. In ihm entdecken wir ein rechtwinkliges Dreieck, das uns erlaubt die trigonometrischen Funktionen anzuwenden. Es hat die Hypotenuse, die dem Radius \(r\) des Kreises und die Gegenkathete (zu \(alpha\)), die der halben Seitenlänge \(s\) entspricht. Deshalb können wir den Sinus von \(alpha\) aufstellen:

[ sin(alpha) = frac{;;frac{s}{2};;}{r} quad rightarrow quad s = 2r sin(alpha) ]

Vom Winkel \(alpha\) wissen wir, dass er der Hälfte eines Zwölftels des ganzen Kreises entspricht, denn das betrachtete rechtwinklige Dreieck ist die Hälfte eines Kuchenstücks, das genau einem Zwölftel des ganzen Kuchens entspricht:

[ alpha = frac{;;frac{360°}{12};;}{2} = frac{180°}{12} ]

Der Umfang des \(12\)-Ecks ist somit:

[ U_{12} = 12 cdot s = 12 cdot  big(2r sin(alpha)big) = 12 cdot 2r cdot sinBig(frac{180°}{12}Big) ]

Für ein allgemeins \(n\)-Eck gilt mit \(d=2r\):

[ U_n = n cdot d cdot sinBig(frac{180°}{n}Big) ]

und damit erhalten wir eine Berechnungsformel für die Zahl \(pi\), die dem Verhältnis von Kreisumfang \(U\) zu Durchmesser \(d\) entspricht. Der Umfang, den wir haben ist nicht genau gleich dem Kreisumfang, sondern nur eine Näherung. Je grösser \(n\), desto genauer sind wir beim Kreisumfang und desto näher entspricht das Resultat der Zahl \(pi\):

[ pi = frac{U}{d} approx frac{U_n}{d} = n cdot sinBig(frac{180°}{n}Big) ]

In der nachfolgenden Tabelle sind die Werte für \(n\)-Ecke berechnet, wobei die Anzahl Ecken immer verdoppelt wurde. In der letzten Zeile haben wir ein \(1536\)-Eck, dessen Verhältnis von Umfang \(U_{1536}\) zu Durchmesser \(d\) der Zahl \(pi\) auf fünf Stellen nach dem Komma entspricht!

\(n\)	\(U_n / d\)	\(Delta %\)
3	2.59808	-54.4%
6	3.00000	-14.2%
12	3.10583	-3.6%
24	3.13263	-0.89%
48	3.13935	-0.22%
96	3.14103	-0.06%
192	3.14145	-0.01%
384	3.14156	-0.004%
768	3.14158	-0.0009%
1536	3.14159	-0.0002%

Im Taschenrechner ist die Zahl \(pi\) auf viele Stellen nach dem Komma gespeichert, so dass wir von nun an diese Zahl einfach abrufen können und sie in unseren Berechnungen verwenden können. Die Genauigkeit ist zwar beschränkt, aber für unsere Zwecke mehr als ausreichend.

Berechnung von π mit einer Reihe

Wir haben gelernt, dass die harmonische Reihe erstaunlicherweise divergiert, d.h. deren unendliche Summe ebenfalls unendlich ist. Dann habe ich aber angemerkt, dass die Reihe von \(a_n=\frac{1}{n^2}\) nicht mehr divergiert. Nicht nur das. Sie konvergiert sogar zu einem erstaunlichen Zahlenwert:

\[ \sum_{n=1}^{\infty} \frac{1}{n^2} \quad = \quad \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + … \quad = \quad \frac{1}{1} + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + … \quad = \quad \frac{\pi^2}{6} \]

Auf diese Weise kann die Zahl \(\pi\) berechnet werden. Wir müssen allerdings in der Reihe sehr weit fortschreiten, um eine einigermassen akzeptable Näherung an unser \(\pi = 3.1416\) zu erhalten.

\(n\)	1	2	3	10	100	500	1000	…
\(a_n\)	1	0.25	0.1111	0.01	0.0001	0.000004	0.000001	…
\(s_n\)	1	1.25	1.3611	1.5498	1.6350	1.6429	1.6439	…
Näherung	2.4495	2.7386	2.8577	3.0494	3.1321	3.1397	3.1406	…