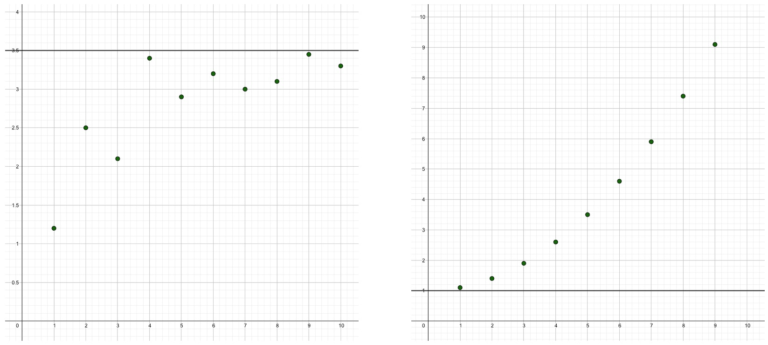
Folgen
Ordnung von Zahlen Die erste Folge, die du je gelernt hast, ist die Folge der natürlichen Zahlen: \[ 1, \, 2, \, 3, \, 4, \, 5, \, …. \] Jede Zahl hat ihren ganz bestimmten Platz. Wir können jederzeit auch sagen, welche Zahl an 27. Stelle steht. Bei dieser Folge ist es einfach: natürlich…