Das Wichtigste in Kürze

Ist die Folge so definiert, dass von einem Glied zum nächsten, immer mit dem gleichen Faktor $q$ multipliziert wird, so spricht man von einer geometrischen Folge.

Die rekursive Definition der geometrischen Folge ist:

\[ a_n = a_{n-1} \cdot q \]

Die explizite Definition der geometrischen Folge ist:

\[ a_n = a_1 \cdot q^{(n-1)} \]

Die geometrische Folge konvergiert, wenn: $|q| < 1$

Häufigste Fragen

Wenn von einem Folgeglied zum Nächsten mit einem konstanten Faktor $q$ multipliziert wird, dann ist die Folge eine geometrische Folge. Beachte, dass dieser Faktor auch $q<1$ oder sogar $q<0$ sein kann, z.B.

\[ (a_n) = 4,\,8,\,16,\,32,\,64,\,… \quad (q=2) \]

\[ (b_n) = 3,\,1.5,\,0.75,\,0.375,\, … \quad (q=0.5) \]

Eine geometrische Folge ist analog zu einer Exponentialfunktion, wo die Werte der Folgeglieder exponentiell wachsen oder exponentiell abfallen.

Ja. Wenn der absolute Betrag des Faktors $q$ kleiner als 1 ist, also $|q| < 1$, z.B.

\[ (a_n) = 8,\,4,\,2,\,1,\,0.5,\,0.25,\,… \quad (q=0.5) \]

Mit $q=0.5$ multiplizieren heisst eigentlich mit 2 dividieren. Dadurch wird das nächste Folgeglied immer kleiner und die Folge konvergiert gegen den Grenzwert null.

Für $|q|>1$ “explodiert” die Folge, d.h. sie ist dann divergent.

Bei der arithmetischen Folge wird von einem Folgeglied zum nächsten ein konstanter Wert $d$ hinzu addiert. Dieser Wert kann auch negativ sein. Er muss aber für die ganze Folge konstant sein, z.B.

\[ (a_n) = 10,\, 25,\, 40,\, 55,\, 70,\, … \quad (d=15) \]

Bei einer geometrischen Folge wird von einem Glied zum Nächsten mit einem konstanten Faktor $q$ multipliziert, der natürlich auch $q<1$ oder sogar $q<0$ sein kann, z.B.

\[ (a_n) = 5,\, 25,\, 125,\, 625,\, … \quad (q=5) \]

\[ (b_n) = 4,\,-2,\, 1,\, -\frac{1}{2},\, \frac{1}{4},\, … \quad (q=-\frac{1}{2}) \]

Definition

Die geometrischen Folgen bilden, wie die arithmetischen Folgen, eine Familie von Folgen mit einer gemeinsamen Eigenschaft.

Bei einer geometrischen Folge erhält man das nächste Glied, indem man immer das vorhergehende Glied mit dem konstanten Faktor \(q\) multipliziert.

Wenn also von einem Folgeglied zum Nächsten immer eine Multiplikation mit dem gleichen Faktor \(q\) vollzogen wird, handelt es sich um eine geometrischen Folge.

Beispiel

Zeige, dass die Folge \(1.5, 3, 6, 12, 24, ….\) eine geometrische Folge ist.

Wir sehen, dass von einem Glied zum nächsten, immer mit 2 multipliziert wird. Somit ist

\[ q=2 \]

Der Faktor \(q\) ist konstant, so dass es sich um eine geometrische Folge handelt.

Konvergenz

Beachte, dass dieser Faktor auch kleiner als eins sein kann. Bei einem Faktor \(q=\frac{1}{2}\) wird immer mit 2 geteilt. Bei einem Faktor \(q=0.001\) wird immer mit 1000 geteilt etc.

Durch das Teilen, machen wir den Folgewert immer kleiner, so dass die Folge gegen den Grenzwert null konvergiert. Deshalb ist \(|q| < 1\) die Bedingung für Konvergenz.

Der Faktor \(q\) kann auch negativ sein, wodurch sich das Vorzeichen die ganze Zeit abwechselt, z.B.

\[ (a_n) = 2,\,-6,\,18,\,-54,\,162,\, … \quad (q=-3) \]

Das Kriterium der Konvergenz funktioniert auch für ein negatives \(q\) mit dem Konvergenzkriterium \(|q|<1\), z.B.

\[ (b_n) = 4, \,-2,\, 1,\, -0.5,\, 0.25,\, -0.125,\, … \quad (q=-0.5) \]

Wir sehen ein dauernd wechselndes Vorzeichen. Jedoch konvergiert die Folge trotzdem, von beiden Seiten, zum Grenzwert null hin.

Rekursive Definition

Aus der Definition der geometrischen Folge erhalten wir sofort die rekursive Definition, d.h. wir nehmen das vorhergehende Folgeglied mit dem Wert \(a_{n-1}\) und multiplizieren es mit \(q\):

\[ a_n = a_{n-1} \cdot q \]

Explizite Definition

Wie bei der arithmetischen Folge, würden wir in gewissen Fällen aber die explizite Definition der Folge bevorzugen, z.B. wenn wir wieder das 94. Glied der Folge berechnen möchten.

Für \(a_2\) müssen wir \(a_1\) einmal mit \(q\) multiplizieren. Für \(a_3\) multiplizieren wir einmal mit \(q\) (und erhalten \(a_2\)) und dann nochmals mit \(q\), d.h. mit \(q^2\). Für \(a_4\) müssen wir \(a_1\) mit \(q^3\) multiplizieren etc. Wir kommen so auf die Formel:

\[ a_{94} = a_1 \cdot q^{93} \]

Auch das können wir wieder von 94 auf \(n\) verallgemeinern und erhalten so die explizite Definition einer geometrischen Folge:

\[ a_n = a_1 \cdot q^{(n-1)} \]

Beachte, dass wir in der obigen Formel auch \(n=1\) einsetzen können. Wir erhalten dann nämlich

\[ a_1 = a_1 \cdot q^{(1-1)} = a_1 \cdot q^0 = a_1 \cdot 1 = a_1 \]

Die Gleichung ist erfüllt. Wir haben dabei benutzt, dass jede Zahl mit Exponent null immer eins ergibt.

Beispiel

In der folgenden Figur misst die Kathete des kleinsten Dreiecks \(s=1\;\text{cm}\). Wie viel misst die Hypotenuse des grössten Dreiecks?

Die erste Hypotenuse des kleinsten Dreiecks hat die Länge \(\sqrt{2}s\). Das zweitkleinste Dreieck hat somit eine Hypotenuse von \(\sqrt{2} \cdot \sqrt{2} s\).

Die Längen der Hypotenusen beschreiben eine geometrische Folge mit \(q=\sqrt{2}\):

\[ h_n = h_1 \cdot q^{(n-1)} = (\sqrt{2}s) \cdot \sqrt{2}^{(n-1)} = s \cdot (\sqrt{2})^n \]

Wir zählen die Hypotenusen ab: Die grösste eingezeichnete Hypotenuse und damit die gesuchte Grösse ist: \(h_6\)

\[ h_6 = s \cdot (\sqrt{2})^6 = s \cdot 2^3 = 8s = \underline{8\,\text{cm}} \]

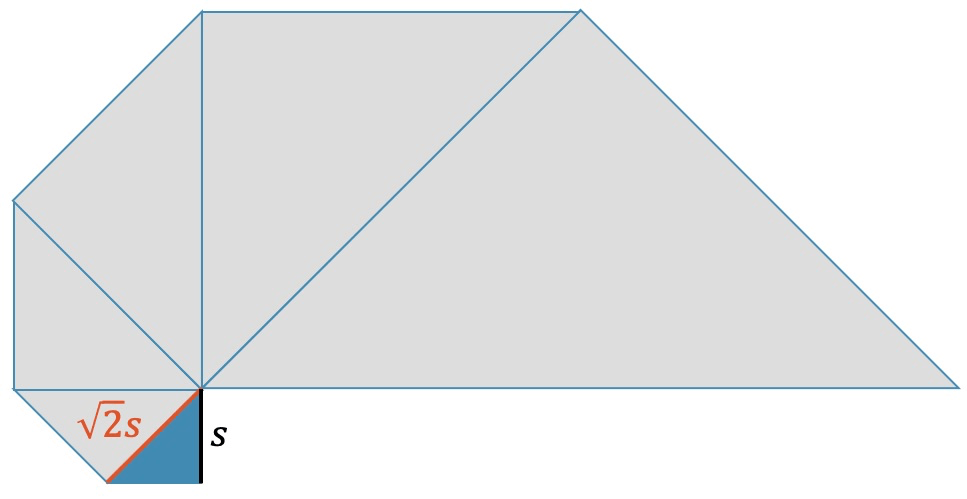
Aufgabensammlung

  • Arithmetische und geometrische Folgen (5009) – Aufg. 3

  • Arithmetische und geometrische Folgen (5009) – Aufg. 4

  • Arithmetische und geometrische Folgen (5009) – Aufg. 5

Lernziele

  • Du kennst die rekursive und explizite Definition der geometrischen Folge.
  • Du kannst geometrische Folgen in passenden Anwendungen einsetzen.

Weitere Links

Arithmetische Folgen (AF)

Geometrische Reihen (GR)

Geometrische Folge (Wikipedia)

David John Brunner

Lehrer für Physik und Mathematik, Zürich | Mehr erfahren

Frage oder Kommentar?

Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.

Kommentar oder Frage schreiben