Grenzwert einer Folge
Von besonderem Interesse sind konvergente Folgen, die sich immer mehr einem Wert annähern. Möglicherweise erreicht die Folge den Wert eigentlich nie oder höchstens in der Unendlichkeit. Ein solcher Wert heisst Grenzwert.
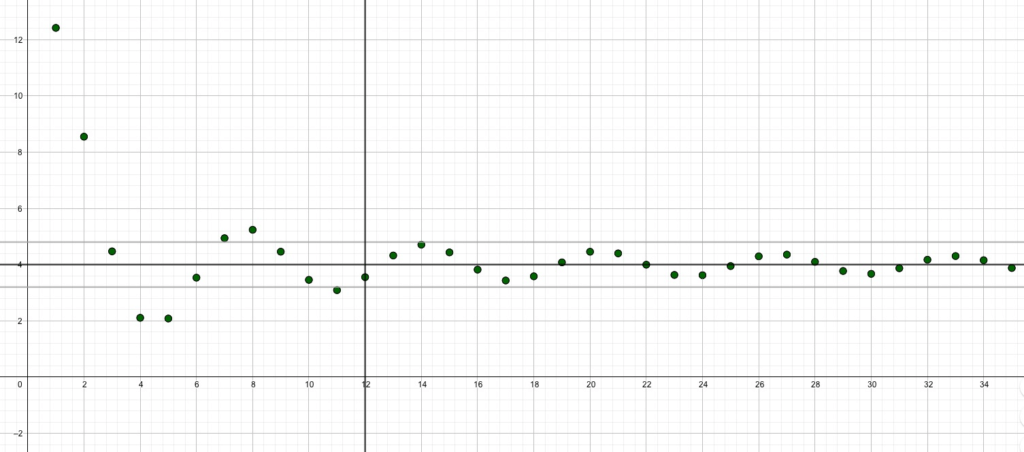
Betrachte die Folge im Diagramm. Die Werte der Folge schwanken anfangs ziemlich ziellos hin und her, dann aber scheinen sie sich an den Grenzwert 4 anzunähern. Für die Mathematiker ist in diesem Beispiel die 4 nur dann ein Grenzwert, wenn es einen “Schlauch” gibt, in welche alle Werte der Folge ab einer bestimmten Position hineinfallen. Hier ist der Schlauch definiert mit \(4 \pm 0.8\), d.h. das Intervall zwischen \(3.2\) und \(4.8\). Tatsächlich sind die Glieder der Folge ab Position 12 innerhalb dieses Schlauchs.
Ein engerer Schlauch und somit eine strengere Bedingung, z.B. innerhalb \(4 \pm 0.2\) wird irgendwann auch erfüllt sein, jedoch ab einer späteren Position. Je weiter hinten in der Folge, d.h. je grösser der Zähler \(n\) für \(a_n\), desto näher sind die Glieder der Folge beim Grenzwert \(a=4\).
Der Grenzwert einer Folge \(a_n\) ist der Wert \(\boldsymbol{a}\). An diesen Wert nähern sich die Glieder der Folge immer mehr an. Je grösser der Zähler \(n\) für die Position in der Folge, desto näher ist \(a_n\) beim Grenzwert \(a\). Meistens erreicht \(a_n\) den Grenzwert \(a\) erst in der Unendlichkeit.
\[ \lim_{n \to \infty} a_n = a \]
So liest du die obige Gleichung: Der limes (=Grenzwert) von \(a_n\) ist, für ein \(n\), das gegen Unendlich läuft, gleich \(a\).
Divergente Folgen haben einen uneigentlichen Grenzwert, weil \(\infty\) keine Zahl ist:
\[ \lim_{n \to \infty} b_n = \pm \infty \]
Beachte, dass beim ersten limes die Definition \(n \to \infty\) stehen sollte. Danach ist es üblich, einfach nur noch \(\lim\) zu schreiben. Es wird dann angenommen, dass weiterhin die gleichen Spezifikationen gelten.
Eigenschaften des limes
Ähnlich wie bei den Summenzeichen, gibt es ein paar Eigenschaften, die für das Rechnen mit Grenzwerten ganz nützlich sind:
\[ \lim (a_n + b_n) = \lim (a_n) + \lim (b_n) \qquad (1) \]
\[ \lim (a_n \cdot b_n) = \lim (a_n) \cdot \lim (b_n) \qquad (2) \]
\[ \lim \Bigl (\frac{a_n}{b_n} \Bigr ) = \frac{\lim (a_n)}{\lim (b_n)} \qquad (3) \]
\[ \lim_{n \to \infty} \Bigl (\frac{1}{n} \Bigr ) = \lim_{n \to \infty} \Bigl (\frac{1}{n^2} \Bigr ) = \lim_{n \to \infty} \Bigl ( \frac{1}{n^3} \Bigr ) = … = 0 \qquad (4) \]
Beispiel
Was ist der Grenzwert der Folge \(a_n = (2+\frac{1}{n})\)?
\[ \lim_{n \to \infty} (2+\frac{1}{n}) = \lim_{n \to \infty} (2) + \lim_{n \to \infty} (\frac{1}{n}) = 2 + 0 = 2 \]
Zuerst haben wir Eigenschaft (1) benutzt, dann Eigenschaft (4).
Berechnung von Grenzwerten
Bei der Berechnung von Grenzwerten gibt es einen Trick: Du ermittelst die höchste vorkommende Potenz im Bruch \(n\) und kürzest den Bruch damit. Du willst ja kein \(n\) oder \(n^2\) im Grenzwert haben, denn der wäre ja Unendlich, wenn du \(n\) gegen Unendlich laufen lässt. Sobald du aber gekürzt hast, findest du ganz viele Brüche in der Art von \(\frac{1}{n}, \frac{1}{n^2}\) etc. vor. Diese sind ganz nützlich, denn sie werden für \(n \to \infty\) zu null.
Beispiel
Berechne den Grenzwert \(a\) der Folge \(a_n\):
\[ a_n = \frac{4n^2+7n+8}{2n^2+3n+7} \]
\[ a = \lim_{n \to \infty} \Bigl ( \frac{4n^2+7n+8}{2n^2+3n+7} \Bigr ) \]
Bevor wir im Zähler und im Nenner einen Grenzwert einsetzen, kürzen wir mit der höchsten, vorkommenden Potenz von unserer Zählvariable \(n\):
\[ a = \lim \Bigl ( \frac{4+\frac{7}{n}+\frac{8}{n^2}}{2+\frac{3}{n}+\frac{7}{n^2}} \Bigr ) \]
Jetzt können wir mit der Eigenschaft (3) den Zähler und den Nenner in einen limes} stecken. Anschliessend verwenden wir Eigenschaft (1), um die Summe im limes} umzuwandeln.
\[ a = \frac{ \lim \Bigl (4+\frac{7}{n}+\frac{8}{n^2} \Bigr ) }{ \lim \Bigl (2+\frac{3}{n}+\frac{7}{n^2} \Bigr ) } = \frac{\lim (4) + \lim (\frac{7}{n}) + \lim (\frac{8}{n^2}) }{\lim (2) + \lim (\frac{3}{n}) + \lim (\frac{7}{n^2}) } \]
Mit Eigenschaft (2) ziehen wir die Faktoren heraus, beispielsweise wird der folgende limes damit gelöst:
\[ \lim \Bigl ( \frac{7}{n} \Bigr ) = \lim \Bigl ( 7 \cdot \frac{1}{n} \Bigr ) = \lim (7) \cdot \lim \Bigl ( \frac{1}{n} \Bigr ) = 7 \cdot 0 = 0 \]
\[ a = \frac{4 + 0 + 0}{2 + 0 + 0} = \frac{4}{2} = 2 \]
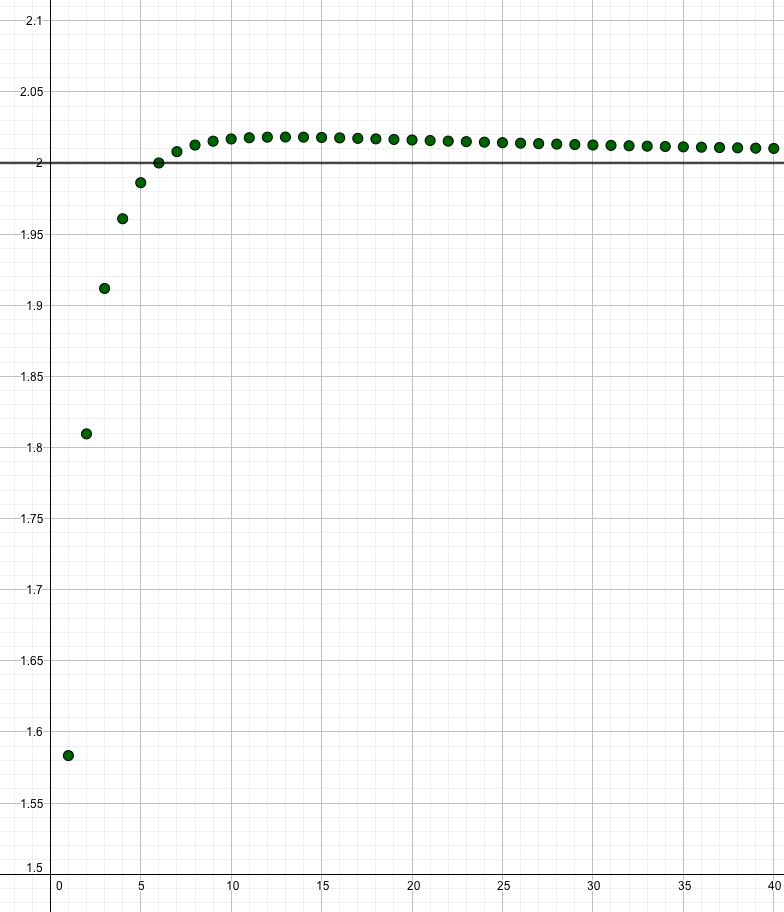
Damit haben wir den Grenzwert bestimmt. Im nachfolgenden Plot sehen wir, dass die Folge den Grenzwert \(a=2\) zunächst überschreitet, sich danach ihm aber annähert.
Dominanzregel
Wir haben gesehen, dass der Grenzwert von \(\frac{1}{n}\) gegen null strebt für sehr grosse \(n\).
\[ \lim_{n \to \infty} \frac{1}{n} = 0 \]
Eigentlich haben wir nichts anderes als einen Bruch mit einem Zähler, der konstant ist und somit immer gleich stark bleibt. Der Nenner nimmt mit wachsendem \(n\) immer mehr zu und wird irgendwann “mächtiger” als der Zähler. Haben wir einen sehr grossen Zähler, so macht der den Bruch so klein, dass am Schluss nur noch null übrig bleibt.
Wenn wir den Zähler von der \(n\)-Potenz her, gleich mächtig machen, dann sieht die Sache wieder ganz anders aus. Wir kürzen den Bruch mit \(n\), so dass der limes von \(\frac{1}{n}\) herausfällt. Übrig bleibt dann nur noch die \(3\).
\[ \lim_{n \to \infty} \frac{3n+1}{n} = 3 \]
Ist der Zähler mächtiger als der Nenner, so divergiert die Folge:
\[ \lim_{n \to \infty} \frac{n^2}{n+2} \rightarrow +\infty \]
Wir dürfen nicht mit \(n^2\) kürzen, da sonst der Nenner null werden könnte, was nicht definiert ist. Mit \(n\) dürfen wir kürzen. Wir erhalten:
\[ \lim_{n \to \infty} \frac{n}{1+\frac{2}{n}} = \frac{\lim (n)}{\lim(1) + \lim(\frac{2}{n})} = \frac{+\infty}{1+0} = +\infty \]
Der Zähler gewinnt und die Folge “explodiert” mit wachsendem \(n\).
\[ \lim_{n \to \infty} \frac{n^3}{e^n} = 0 \]
Hier haben wir ein Kräftemessen zwischen einer dritten Potenz \(n^3\) und einer Exponentialfunktion \(e^n\). Für wachsende \(n\) nehmen beide stark zu. Allerdings nimmt irgendwann die Exponentialfunktion viel stärker zu als die Potenzfunktion. Wenn also die Exponentialfunktion im Nenner über die Potenzfunktion im Zähler gewinnt, dann wird der Bruch gegen null gehen.
\[ \lim_{n \to \infty} \frac{n^3}{\log(n)} = +\infty \]
Umgekehrt ist die Situation, wenn eine Potenzfunktion gegen einen Logarithmus antritt. Auch hier nehmen beide mit wachsendem \(n\) zu, jedoch auf lange Sicht sehr unterschiedlich stark. Der Logarithmus im Nenner nimmt am schwächsten zu und verliert den “Kampf” mit dem Zähler: Der Bruch “explodiert”.
Mit der Dominanzregel vergleichen wir die relative Stärke von Termen in einem Ausdruck, typischerweise in einem Bruch. Wir wenden dabei folgende Rangordnung der Mächtigkeiten an:
Exponential > Potenz mit grossem Exponenten > Potenz mit kleinem Exponenten > Logarithmus
Beachte, dass eine Konstante, eigentlich eine Potenz mit Exponent null ist.
Wenn der Zähler “gewinnt”, divergiert die Folge mit dem uneigentlichen Grenzwert \(\pm \infty\).
Gewinnt der Nenner, so ist der Grenzwert null. Gleich starke Zähler und Nenner enden meist in einem Vielfachen von \(1\).
Beispiel
Bestimme den Grenzwert von
\[ a_k = \log(k) \cdot \frac{k-1}{k^2-2k+1} \quad \text{für} \quad k \to \infty \]
Wir erkennen im Nenner des Bruchs die binomische Formel \(a^2 – 2ab + b^2\) und zerlegen den Nenner deshalb in seine Faktoren, so dass wir einen im Bruch kürzen können:
\[ \require{cancel} a = \lim_{k \to \infty} \frac{ \log(k) \cdot \cancel{(k-1)}}{(k -1) \cancel{(k- 1)}} = \lim_{k \to \infty} \frac{ \log(k)}{(k -1)} \]
Jetzt sehen wir, dass ein Logarithmus (Zähler) es mit einer Einer-Potenz (Nenner) aufnehmen will. Der Nenner wird für grosse \(k\) stärker sein. Der Bruch wird deshalb mit wachsendem \(k\) immer kleiner werden, bis er im Unendlichen null ist. Wir schreiben deshalb das fertige Resultat hin:
\[ a = \lim_{k \to \infty} a_k = 0 \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.