Das Wichtigste in Kürze
Wiensches Verschiebungsgesetz: Die Verteilung der Wellenlängen der Wärmestrahlung hat ein Intensitätsmaximum bei der Wellenlänge \(\lambda_{max}\). Je nach Temperatur verschiebt sich diese Wellenlänge maximaler Intensität:
\[ \lambda_{max} = \frac{2.898 \cdot 10^{-3}\;\text{K m}}{T} \]
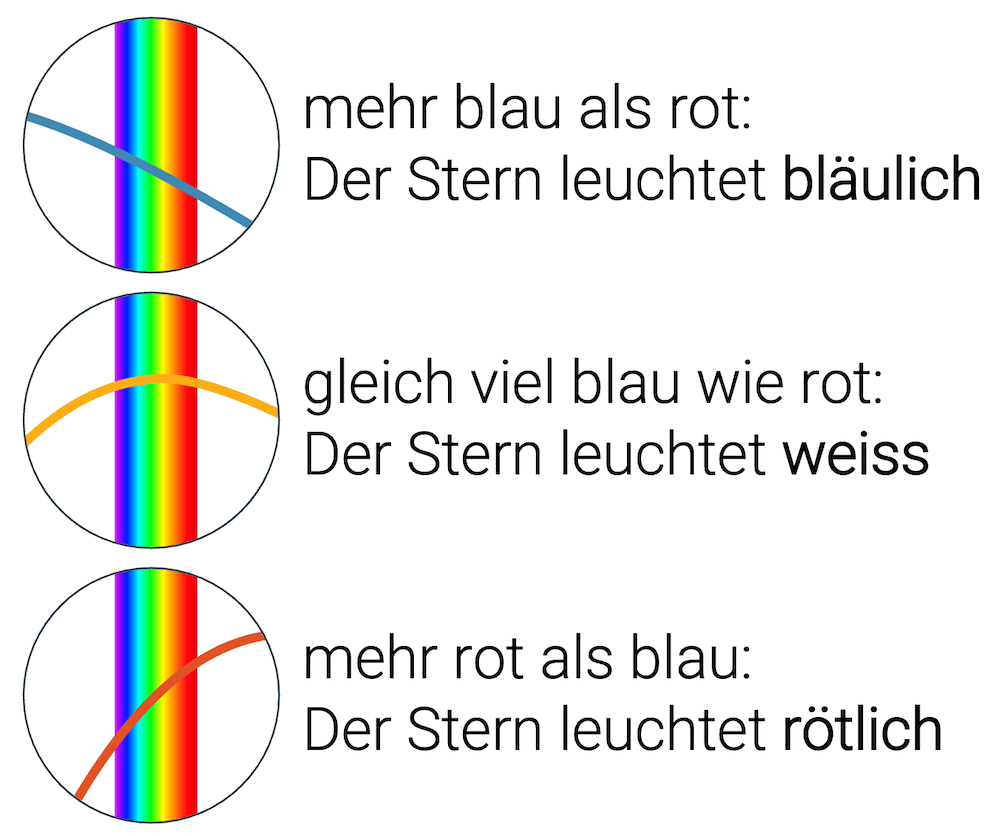
Für höhere Temperaturen verschiebt sich das Spektrum der Wärmestrahlung immer mehr zu kürzeren Wellenlängen hin. Meistens ist die ganze Wärmestrahlung im Infrarotbereich. Ab einer Temperatur von ca. 400 °C sind erste Anteile der Strahlung auch im sichtbaren Bereich und wir erkennen ein erstes rotes Glühen. Mit steigender Temperatur erscheint die Wärmestrahlung rot, gelblich, dann weiss, hin zu bläulich.
Das Wiensche Verschiebungsgesetz ist nach seinem Entdecker, dem deutschen Physiker Wilhelm Wien (1864 – 1928) benannt, der für seine Forschung im Bereich der Wärmestrahlung 1911 den Nobelpreis für Physik erhielt. Es beschreibt die Verschiebung des Spektrums der Wärmestrahlen in Abhängigkeit der Temperatur.
Die Wärmestrahlung eines Körpers bei einer bestimmten Temperatur hat nicht nur genau eine Wellenlänge, sondern ist ein Gemisch von elektromagnetischer Strahlung mit verschiedenen Wellenlängen. Dieses Gemisch kann mit einer Verteilung der vorkommenden Intensität über die Wellenlänge beschrieben werden.
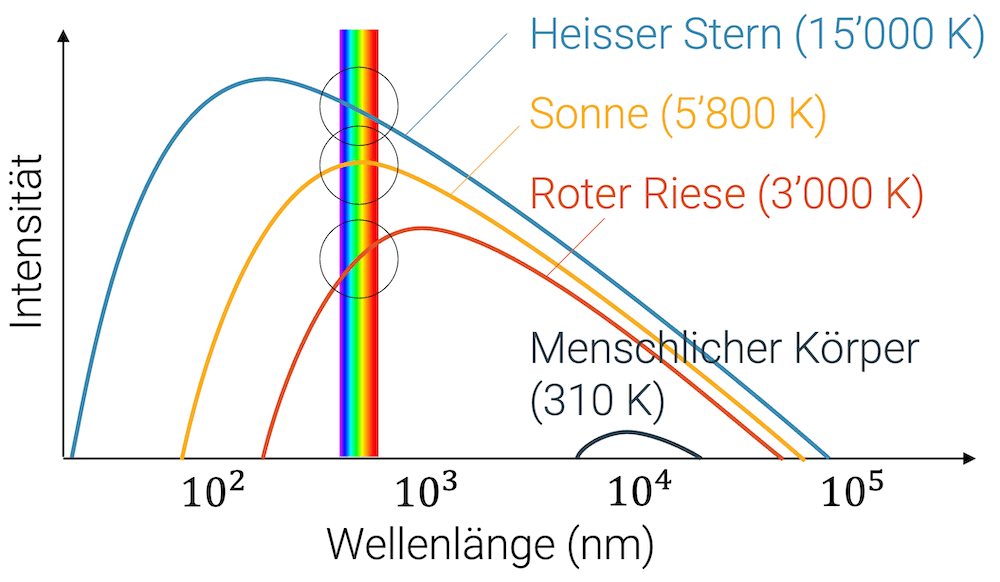
Wien entdeckte die Gesetzmässigkeit zwischen der Wellenlänge des Maximums \(\lambda_{max}\), d.h. die Wellenlänge, die am stärksten vertreten ist und der Temperatur \(T\). Sein Gesetz ist ein empirisches Gesetz, d.h. es passt zu Messungen, berücksichtigt aber kein darunter gelegenes Modell.
Anwendungsbereich: Das Wiensche Gesetz gilt näherungsweise für Wellenlängen bis max. \(750\;\text{nm}\).
Wir können die Wärmestrahlung bei ”normalen” Temperaturen nicht sehen, weil sie ausschliesslich im infraroten Bereich ist. Mit speziellen Wärmebildkameras kann diese Strahlung sichtbar gemacht und mit Farben eingefärbt werden. Wir erhalten mit sog. Wärmebildern einen Eindruck davon, wie es aussehen würde, wenn wir Infrarotstrahlung sehen könnten.
Wenn die Temperatur genug gross ist, kann Wärmestrahlung auch ohne technische Hilfsmittel gesehen werden. Das Glühen ab Temperaturen von 400 °C, z.B. von heisser Kohle oder heissem Metall, wird Inkandeszenz genannt.
Alle Körper emittieren Wärmestrahlung. Je heisser, desto weiter verschiebt sich die Verteilung der Wellenlängen hin zu kurzen Wellenlängen.
In einer Schmiede können mit dem Blasebalg Temperaturen von über 1000 °C erreicht werden, wo das Glühen schon fast als ”weiss” empfunden wird (”Weissglut”).
Rotes Glühen bis hin zu Weissglut sind für uns noch bekannt. Darüber würde es anfangen bläulich zu leuchten. Beobachten können wir das an sog. blauen Riesen (z.B. Rigel im Sternbild Orion). Blaue Riesen sind grosse Sterne, die eine sehr hohe Oberflächentemperatur haben.
Andererseits haben die roten Gasriesen, also Sterne die am Ende ihres Lebenszyklus’ sind, tiefere Temperaturen, denn die maximale Wärmestrahlungsintensität befindet sich bei ihnen bereits im Infrarotbereich. Wir sehen nur den oberen, sichtbaren Teil der Strahlung, der v.a. bei rot intensiv ist.
Unsere Sonne ist ein Körper mit einer Oberflächentemperatur von 5800 K. Deren Wärmestrahlung enthält Wellenlängen von 10\(^\text{2}\) nm bis knapp 10\(^\text{5}\) nm, d.h. vom UV-Bereich bis in den Infrarotbereich.
Das Maximum der Wärmestrahlung der Sonne ist bei einer Wellenlänge von 500 nm, was sichtbarem Licht entspricht.
Beispiel: Sonnenstrahlung
In der Sonnenstrahlung ist die Wellenlänge von 500 nm am meisten vertreten.
Zeige, dass die Oberfläche eine Temperatur von T = 5800 K haben muss.
Aufgabensammlung
Weitere Links
Wiensches Verschiebungsgesetz (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.