
Streulinsen (oft auch Zerstreuungslinsen oder bikonkave Linsen genannt) sind Scheiben mit gekrümmten Oberflächen aus einem transparenten Material (typischerweise aus Glas), die so geformt sind, dass sie in der Mitte dünner sind als aussen (konkav). Durch die Brechung werden die Lichtstrahlen in der Streulinse so umgelenkt, dass parallele Strahlen nach der Linse auseinander driften, als würden sie dem Brennpunkt vor der Linse entspringen.
Streulinsen finden wir z.B. als Korrekturgläser für Kurzsichtige. Sie finden sich aber auch in Objektiven und anderen optischen Instrumenten.
Streulinsen erzeugen immer aufrechte, verkleinerte, virtuelle Bilder. Für sie gilt auch die Linsengleichung, mit welcher die Bildweite \(b\) aus der Gegenstandsweite \(g\) und der Brennweite \(f\) der Linse berechnet werden kann. Die Brennweite wird aber negativ eingesetzt, da der Brennpunkt auf der “falschen” Seite der Linse ist:
\[ \frac{1}{f} = \frac{1}{g} + \frac{1}{b} \quad \mathrm{mit} \quad f<0 \]
Strahlenverlauf
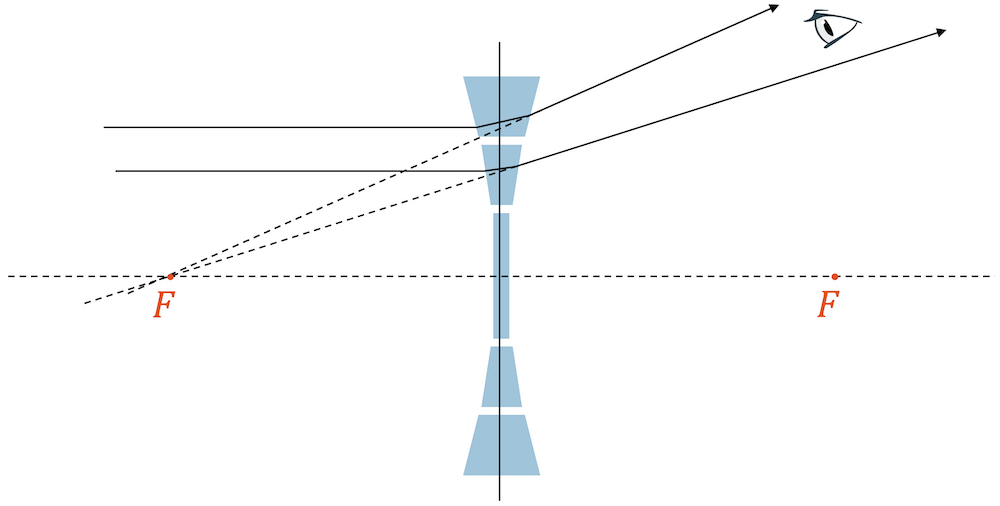
Wir stellen uns vor, dass die Streulinse aus vielen trapezförmigen Prismen zusammengesetzt ist. Dank dem Brechungsgesetz verstehen wir, dass die parallelen Strahlen nach der Linse auseinander laufen. Nur der Lichtstrahl auf der optischen Achse trifft genau senkrecht auf das Medium der Linse und behält deshalb seine Richtung. Die Parallelstrahlen verlaufen nach der Streulinse in der Art, als kämen sie vom gleichen Ursprung, dem Brennpunkt F vor der Linse.
Auch die Streulinsen haben immer zwei Brennpunkte, die auf der optischen Achse und im gleichen Abstand von der Linsenebene liegen (Brennweite \(f\)). Stark gekrümmte Linsen brechen die Strahlen stark und haben eine kurze Brennweite.
Wichtigste Strahlen
Parallelstrahl \(^ \rightarrow\) Brennpunktstrahl (Brennpunkt vor der Linse)
Brennpunktstrahl (Brennpunkt nach der Linse) \(^ \rightarrow\) Parallelstrahl
Mittelpunktstrahl \(^ \rightarrow\) Mittelpunktstrahl
Bild der Streulinse
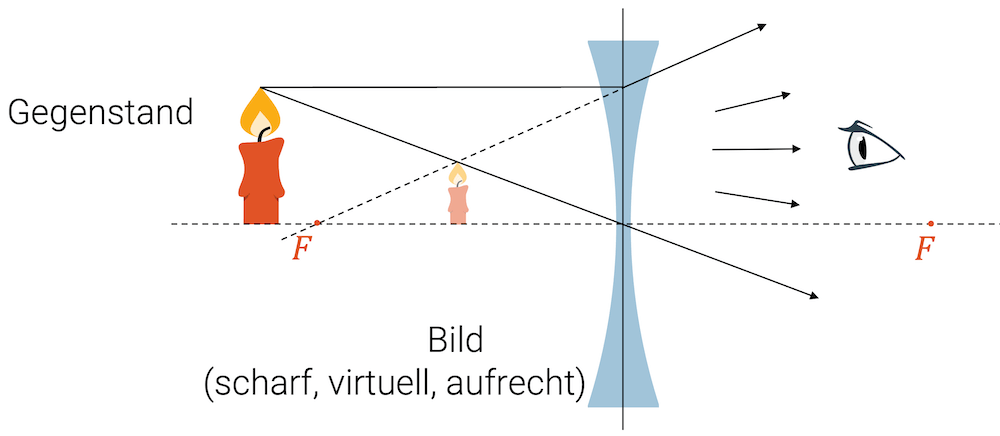
Die Spitze des Gegenstands sendet Lichtstrahlen (z.B. durch Streuung) in alle Richtungen. Beachten Sie: Es ist in der Optik üblich, die Brechung an den beiden Linsenoberflächen nur mit einer einzige Brechung in der Linsenebene darzustellen. Oft wird der Linsenkörper gar nicht gezeichnet.
Betrachten wir den Parallel- und den Mittelpunktstrahl: Der Parallelstrahl wird zu der Verlängerung eines Brennpunktstrahls (vom Brennpunkt vor der Linse aus). Der Mittelpunktstrahl wird, wie bei allen Linsen üblich, nicht gebrochen. Beide Strahlen laufen nach der Linse auseinander und können deshalb kein reelles Bild erzeugen. Für den Betrachter hinter der Linse scheinen sie aber von einem gemeinsamen Bildpunkt zu kommen. Dieser Bildpunkt erlaubt uns das virtuelle Bild vor der Linse zu konstruieren.
Bei der Streulinse gibt es immer virtuelle, aufrechte Bilder, die kleiner sind als der Gegenstand selber. Sie kennen, im Vergleich zur Sammellinse keinen “Kipppunkt”, wo ein aufrechtes Bild zu einem umgekehrten Bild wechselt oder umgekehrt.
Linsengleichung
Mit der Linsengleichung werden die Gegenstandsweite \(g\), die Brennweite \(f\) und die Bildweite \(b\) mit einander verknüpft, d.h. du kannst den Abstand des Bilds vor der Linse mit Brennweite \(f\) berechnen, wenn der Gegenstand in einem bestimmten Abstand \(g\) vor der Linse steht:
\[ \frac{1}{f} = \frac{1}{g} + \frac{1}{b} \]
Speziell an der Streulinse ist der Umstand, dass die Brennweite negativ ist. Da das Bild virtuell ist, wird auch die berechnete Bildweite \(b\) negativ sein. Gemeint ist damit, dass auch das Bild sich vor der Linse befindet.
Beispiel
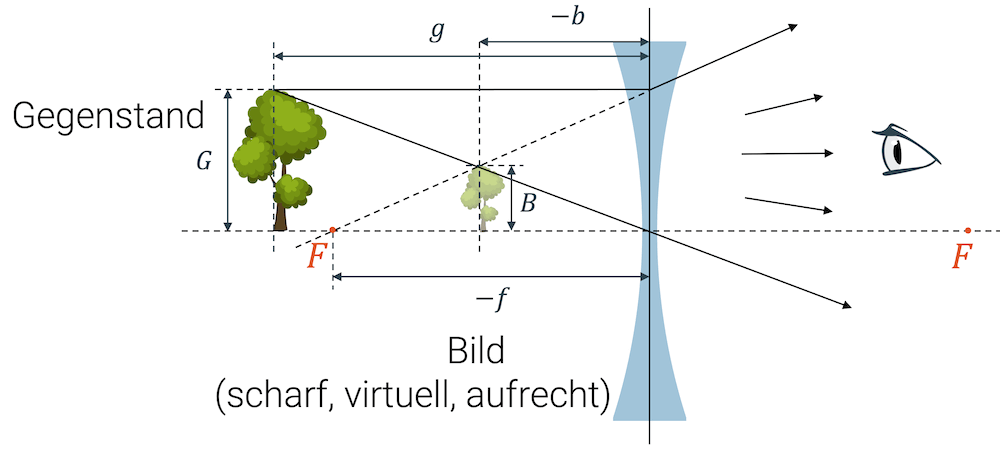
Ein \(g=12\,\mathrm{m}\)-hoher Baum steht im Abstand \(g=10\,\mathrm{m}\) vor einer Streulinse mit Brennweite \(f=-3\,\mathrm{m}\). Wie weit erscheint das Bild des Baums für den Betrachter, wenn er ihn durch die Linse anschaut? Wie gross ist das Bild?
Mit der Linsengleichung erhalten wir:
\[ \frac{1}{b} = \frac{1}{f} – \frac{1}{g} = \frac{g-f}{fg} \]
Nun bilden wir den Kehrwert von \(\frac{1}{b}\) und erhalten:
\[ b = \frac{fg}{g-f} = \frac{(-3\,\mathrm{m}) \cdot 10\,\mathrm{m}}{10\,\mathrm{m} – (-3\,\mathrm{m})} = \frac{-30\,\mathrm{m^2}}{13\,\mathrm{m}} = -\frac{30}{13}\mathrm{m} = -2.3\,\mathrm{m} \]
Die Bildweite ist (wie die Brennweite) negativ, weil das Bild ein virtuelles Bild vor der Linse ist. Das Bild des Baums erscheint dem Betrachter 2.3 Meter vor der Linse.
Für die Ermittlung der Grösse des Bilds \(B\) betrachten wir die beiden rechtwinkligen Dreiecke, die mit dem Mittelpunktstrahl entstehen: Das erste Dreieck hat die Höhe \(G\) und die Grundseite \(g\). Die Höhe des zweiten Dreiecks ist \(B\) und die Grundseite ist \((-b)\), da \(b\) negativ ist.
Beide Dreiecke sind ähnlich, so dass deren Seiten gemäss Strahlensatz zu einander proportional sind. Wir können deshalb schreiben:
\[ \frac{G}{g} = \frac{B}{(-b)} \]
Wir lösen nach der Unbekannten \(B\) auf und setzen die Zahlenwerte ein:
\[ B = \frac{(-b)}{g} \cdot G = \frac{2.3\,\mathrm{m}}{10\,\mathrm{m}} \cdot 12\,\mathrm{m} = \underline{2.8\,\mathrm{m}} \]
Dieses Resultat ist typisch für eine Streulinse: Das Bild ist kleiner und näher zum Betrachter, als der Gegenstand.
Simulation
Bewege die Spitze des Gegenstands Object mit der Maus. Für die Streulinse bewegst du den Brennpunkt Focus‘ nach rechts, auf die andere Seite der Linse.
Simulation der Strahlenverläufe durch eine Sammel- bzw. Streulinse
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.