Der Brechungsindex \(n\) ist eine Materialgrösse. Er gibt an, um welchen Faktor die Wellengeschwindigkeit des Lichts im Vergleich zum Vakuum verlangsamt ist.
Lichtgeschwindigkeit in einem Medium mit Brechungsindex \(n\):
\[ u_1 = \frac{c}{n} \]
Trifft Licht (oder eine andere Form von Welle) auf eine Grenzfläche eines Mediums mit anderem Brechungsindex, so verändert sich die Wellenlänge und es entsteht das Phänomen der Brechung.
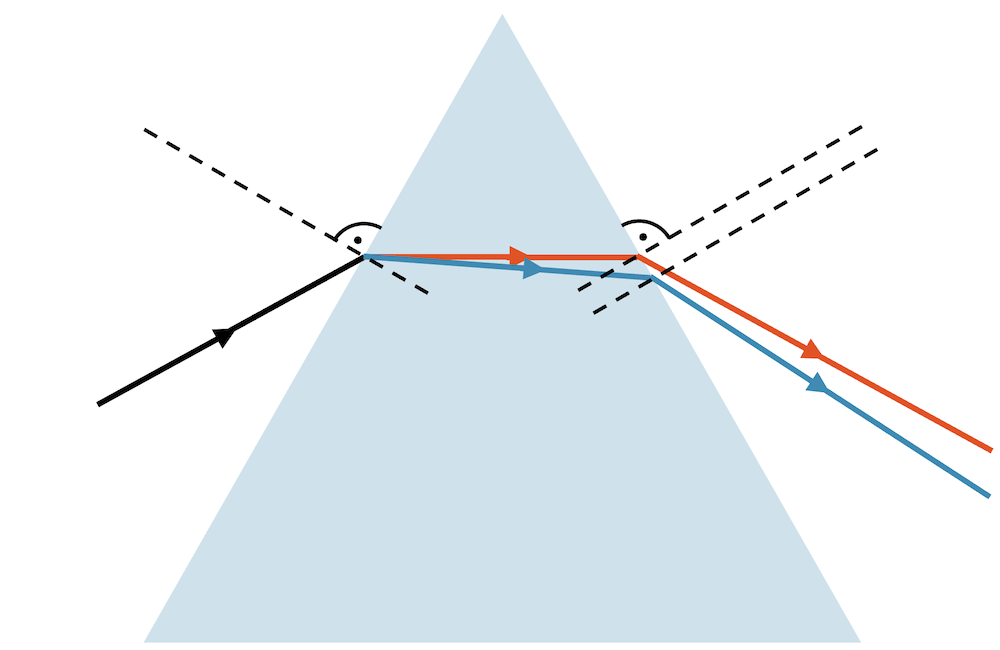
Der Brechungsindex ist meistens abhängig von der Frequenz des Lichts (Dispersion), so dass unterschiedliche Farben verschieden stark gebrochen werden. Im Glasprisma ist langwelliges rotes Licht etwas weniger verlangsamt als kurzwelliges blaues Licht. Der Brechungsindex von Glas ist für rotes Licht deshalb leicht kleiner als für blaues Licht, so dass blaues Licht stärker gebrochen wird als rotes Licht. Für die anderen Farben liegen die Brechungsindizes zwischen den beiden Extremen, so dass das Prisma das weisse Licht in alle Regenbogenfarben aufteilt.
Definitionen
Abkürzung: \(n\)
Einheit: \([n] = -\) (Zahl)
Brechungsindizes verschiedener Materialien
| Material | Brechungsindex \(n\) |
| Vakuum | 1 (exakt) |
| Luft | 1.0003 \(\approx\) 1 |
| Wasser | 1.33 |
| Glycerin | 1.47 |
| Fensterglas | 1.52 |
| Diamant | 2.42 |
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.